Thread by @genkuroki

#Julia言語 Juliaの型について十分な理解がない段階でJuliaで型を明示的に書くと、大抵の場合ろくなことにならないし(バグの原因になる)、理解が進むと、型を明示的に書いた方が良いという考え方自体が技術的に劣っている考え方だと気付きます。

Juliaでは型を明示せずに、型の伝搬で考える。続く

https://twitter.com/mrsekut/status/1372051897079631875

#Julia言語 私自身がやらかした失敗の例

① function f(x::Vector{Float64}) ～ end

のように引数の型を明示した函数を定義し、その函数を使ったプログラムが正常に動作していた。

② @ viewマクロを使った最適化を行った。

③その途端に正常に動いていたプログラムが動かなくなった！😭

続く

#Julia言語 その原因は

function f(x::Vector{Float64}) ～ end

と函数の引数の型を Vector{Float64} に明示的に宣言してしまっていたことが原因です。その「@ viewによる最適化で動かなくなった」という問題は

function f(x) ～ end

に書き直せば解決しました。続く

#Julia言語 数値計算ではなく、文字列処理を多数やっている人なら、私と同様の失敗を

function f(x::String) ～ end

と書いてやらかしていたりすると思います。

SubStringはStringではないので、これだと思わぬ所でプログラムが動かなくなりがち。

@ viewで作ったSubArrayはVectorではない。続く

#Julia言語 上のような失敗は

function f(x::AbstractVector{Float64}) ～ end

や

function f(x::AbstractString) ～ end

と書いていれば防げました。

しかし、

function f(x::AbstractVector{Float64}) ～ end

には別の致命的な欠点があります。続く

#Julia言語 は composability で優れています。

具体的には、例えば、Juliaで適切に書かれた微分方程式のソルバを使っていれば、後でパラメータの値に幅を持たせたときの微分方程式の解の挙動の視覚化を新たなコードを追加せずに実行できます。

以下のリンク先スレッドに実例があります。続く

https://twitter.com/genkuroki/status/1371086156129918981

#Julia言語 新たなコードを追加せずに、パラメータの値に幅を持たせた場合を扱うには、「幅を持つ数値」の型を定義し、微分方程式のソルバにそういう型の数値を使った場合の微分方程式を解かせればよい。

https://twitter.com/genkuroki/status/1371087072019157002

#Julia言語 だから、

function f(x::Vector{Float64}) ～ end

のように書いた途端に、Float64型専用の「幅を持つ数値」の型では使えない函数になってしまい、Juliaの強みであるcomposabilityを活かせなくなってしまいます。続く

#Julia言語 Float64型や「幅を持つ数値」の型の多くがReal型のsubtypeであると知った人が

function f(x::Vector{Real}) ～ end

と書くと、ほとんど全く使えない函数が出来上がります。なぜならば、Vector{Float64}型はVector{Real}型のsubtypeにならないからです。続く

#Julia言語

function f(x::Vector{Real}) ～ end

ではなく

function f(x::Vector{<:Real}) ～ end

と書かなければいけないことを知っておく必要がある。

以上の解説をよんで「うわ！こんな面倒ならJuliaを使えない！」と思った人は私の仲間です！(笑)

シンプルな解決策があります！続く

#Julia言語

シンプルな解決策：函数の引数の型の指定は必要最小限にする。基本的に函数の引数の型の指定をしないことにする。

無駄な記述が減ってコードもすっきり見易くなります(笑)
↑
これは冗談ではないです。

函数の引数の型の指定の有無はJuliaでは計算効率に何も影響しません。続く

#Julia言語 たたし struct の定義で

struct Foo
a
b
end

と書くのはダメです。計算速度が露骨に落ちます。しかし、

struct Foo
a::String
b::Float64
end

と書くと、上で説明したのと似た問題が起こる場合がある。

struct Foo{A, B}
a::A
b::B
end

がお勧め。

#Julia言語 要するに、具体的な型名をほとんど書かずに、Juliaの便利な機能(speed! composability! ...)だけを美味しく利用することができるわけです。

しかし、コードを書くときに支払うべき新たな税金はあります。

それはtype stabilityの確保。

型の伝搬の安定性と言う方が分かり易いかも。

#Julia言語 は、JITコンパイラなので、函数の実行時に完全にわかっている引数の具体的な型に合わせて最適化されたネイティブコードにコンパイルすることを試みます。

#Julia言語 例えば f(x)=x^2 をf(123)と実行するとxがInt64型専用のネイティブコードを、f(12.3)ならFloat64型専用のネイティブコードを、f("abc")ならString型専用のネイティブコードにコンパイルしてから実行します。(f("abc")は"abcabc"になる)

#Julia言語 適切にコードを書けば、引数の具体的な型から函数の値の具体的な型が一意的に決まります。これが型安定の最も易しい場合です。

f(x)=x^2よりも複雑で局所変数を持つ函数では、局所変数の具体的な型が引数の型から一意的に決まるように(型安定になるように)書くことが、Juliaの流儀です。

#Julia言語 要するに

function f(x)
～
end

のように引数の型をしてせずに函数を書くときには、xの具体的な型が想定内の何であっての、その具体的な型が函数内の他の変数の具体的な型を適切かつ一意的に決まるように書くことを目指します。

型の明示ではなく、型の伝搬で勝負するわけです。続く

#Julia言語 型の伝搬の仕方を人間の頭の中でシミュレートし切るのは無理です。型の伝搬の様子を表示してくれる便利なコマンド(マクロ)があります。

f(x) = x^2

@ code_warntype f(2)

@ code_warntype f(2.0)

@ code_warntype f("a")

を実行してみると良いと思います。@ 直後の空白は削除。

#Julia言語 @ code_warntype は型の伝搬の安定性が崩れている場合には強い警告色でその部分を表示してくれます。

ごちゃごちゃっと意味不明の複雑な表示を細かく見ずに、強い警告色で表示された部分がもとのコードのどの部分に対応するかのみに意識を集中すれば、初心者であっても実用になります。

#Julia言語 例えば

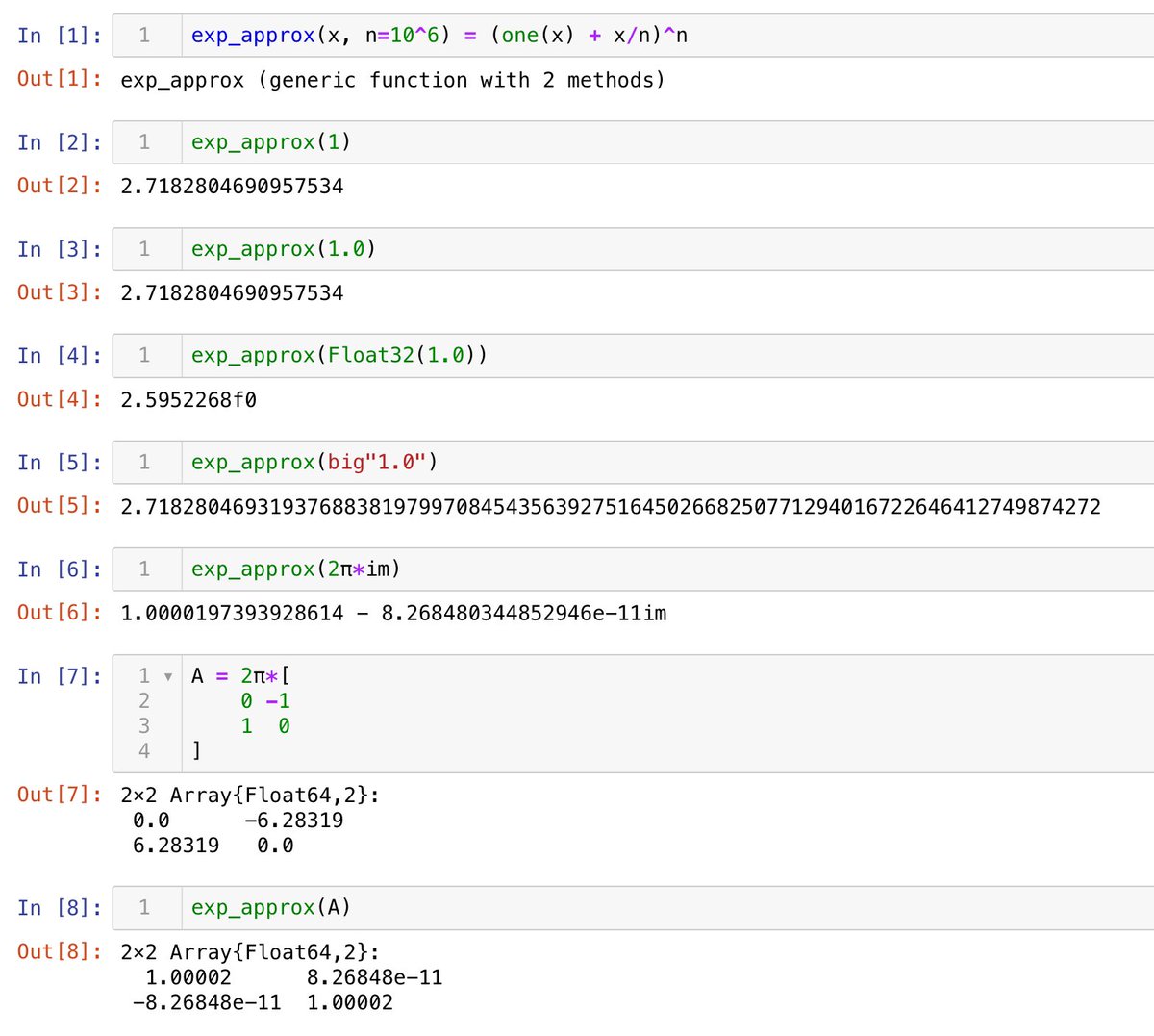
exp_approx(x, n=10^6) = (one(x) + x/n)^n

というコードは近似的にexp(x)を計算してくれる函数です。

one(x)は多くの場合にxと同じ型の1になる。このように書いておくと、正方行列xにも適用可能になる(添付画像1)。

添付画像2は@ code_warntypeの例。

#Julia言語 微分方程式のソルバは本質的に上の exp_approx(x, n) の一般化とみなせます。

Juliaで適切に微分方程式のソルバを書けば、exp_approx(x, n)のように、Float64, Float32, BigFloat, ComplexF64, Matrix{Float64}, etc.と多数の型の入力に対応しているものを作れます。

#Julia言語 そして、そのソルバは実行時に入力の具体的な型に合わせて最適化されたネイティブコードにコンパイルされてから実行されることになります。

入力が「幅を持つ数値」なら「幅を持つ数値」の型専用のネイティブコードにコンパイルされてから実行されます。

#Julia言語 これは同じようなコードを繰り返し書く手間を大幅に減らしてくれます！

そして、それを支える基本的な考え方は、型の明示で頑張ろうとせずに、型の伝搬を適切に記述するという考え方です。

上の例では one(x) のような書き方が型の適切な伝搬を支えています。

#Julia言語 では、「Float64型を与えて、Float64型の値を返す函数を書く」という発想をせずに、

* 引数の具体的な型に合わせて、適切な型の値を返す函数を書く。

* 函数の引数の具体的な型から函数内の局所変数の型が自動的に決まるように書く。

のように考えます。

#Julia言語 NASAでJuliaがどのように使われているかについては以下のリンク先のスレッドを参照。

https://twitter.com/genkuroki/status/1371085530398564353

#Julia言語 固定されたX,Yについて

f : X → Y

を定義するという考え方ではなくて、

f : (?) → Φ(?)

を定義するという発想。

?として具体的な型を与えると、fの終域 Φ(?) が具体的な型として決まるように書きたい。(fの定義中で間接的にΦを記述する。)

fの型は「fそのもの」になる。

#Julia言語

scrapbox.io/mrsekut-p/2021…
【「Juliaの型はパフォーマンスの為だけに書く」というのをどこかで見た記憶がある】

「Juliaの型はパフォーマンスの為だけに書く」は誤り。

「Juliaではパフォーマンスの為に型を書く必要がない」なら概ね正しいです。型を書かずにCと同程度に速い。続く

https://twitter.com/mrsekut/status/1372051897079631875

#Julia言語 函数f(x)が1つも型を明示せずに書かれていたとしても、引数xの具体的な型が与えられたならば、その具体的な型の情報をコンパイラは利用できます。続く

#Julia言語 函数f(x)のコードが型の伝搬が安定になるように書かれていれば、函数f(x)の定義内の引数以外のモノの型も決まり、具体的型が全部わかっている状態でf(x)のコンパイルが可能になる。

実際にそうなればJuliaの函数はCの函数とほぼ同じ速さで動く。

これが型を明示しなくても速い仕組み。

#Julia言語 Juliaでの函数の引数の型の明示は、多重ディスパッチを利用する為に使われます。例えば、

f(a, x) = a*x
f(a::Integer, x::AbstractString) = x^a

と定義すると

f(3, 1.2) → 3.6
f(3, "hoge") → "hogehogehoge"

となります。Juliaでは文字列の冪は文字列の繰り返しになる。続く

https://twitter.com/mrsekut/status/1372051897079631875

#Julia言語

f(a, x) = a*x
f(a::Integer, x::AbstractString) = x^a

のとき

f(3, 5) → 15

となるのですが、さらに

f(a::Integer, x::Integer) = x + a

と定義すると

f(3, 5) → 8

となる。

同名の函数であっても引数達の型の組み合わせが違っていたら別の仕事をさせることができる。続く

#Julia言語 特に、同名の函数 f(a, x) は a の型が違えば別のメソッドになるので(Juliaの場合はxの型が違ってもそうなる)、f(a, x) のaだけを特別扱いして、a.f(x)と書くことを許せばよくあるOOP型の言語に近くなります。

しかし、f(a, x)のaだけを特別扱いするのはJuliaのスタイルとは相性が悪い。

#Julia言語 Juliaでは、f(a::型名1, x::型名2) のように型を明示してもパフォーマンスには何の足しにもならないのですが、同名の函数fにa, xの型の組み合わせごとに別のメソッドを割り振ることができます。

これは実際に使ってみると、ものすごく便利。

a.f(x)のスタイルでは苦しい場合がある。

#Julia言語

以上で説明したように、

* 多重ディスパッチ(同名の函数 f(x, y, z) にx,y,zの型の組み合わせごとに別のメソッドを割り振れること)

や

* f(a, x) ↔ a.f(x) の対応

について知れば、「クラスは別に必要ない」ということが比較的容易に分かると思います。

#Julia言語

メソッド f が a の所有物で a.f(x) と書くスタイル

と

a, x の型の組み合わせごとに f(a, x) で実行されるメソッドを違うものにできるというスタイル (f は a の所有物ではない)

の違い。後者がJuliaのスタイル。後者のスタイルで前者のスタイルはシミュレートできる。

#Julia言語

* パフォーマンスのために函数の定義で型を明示する必要はない。

* f(x, y, z)のxだけを特別扱いしてx.f(y, z)と書くスタイルを採用する必要もない。

* x, y, z を平等に扱い、x, y, zの型の組み合わせごとに f(x, y, z) で実行されるメソッドを違うものにできるスタイルも可能である。

#Julia言語

function f(x::型名) ～ end

と引数の型を書く場合の注意は以上の通り。

それでは返り値の型を

function f(x)::型名 ～ end

と書いた場合についてはどうだろうか？

f(x)::Int = x/10

と

g(x) = typeassert(convert(Int, x/10))

について、f(123)とg(123)は等価！続く

#Julia言語 x=123のとき、x/10は12.3になり、convert(Int, 12.3)はエラーになるので、f(123)もg(123)も実行時にエラーになります。

これもバグの原因になります。

f(x)::Int と定義された函数は多くの場合に動いていたが、たまにエラーで落ちるという動作をするかもしれない。

続く

#Julia言語 f(x)::Int のようなスタイルで書かれた函数は、実行時にエラーにならなくても、型安定性が確保されていないせいで、最後に余計なconvertが実行され、律速段階になってしまうかもしれない。

Juliaでは素直に型安定になるようなコードを書くのがお得。

@ code_warntype での確認は重要。

#Julia言語 「型伝搬の安定性を確認する」という問題に興味を持った人は以下のリンク先達を読むと楽しめると思います。

github.com/aviatesk/JET.jl

zenn.dev/aviatesk/artic…

#Julia言語 型伝搬の安定性の確認は、@ code_warntype や @ code_typed で可能で、バグの洗い出しにも効果有りなのですが、現時点では手動で行っている。しかし、それは大変すぎる場合がある。

JET.jlパッケージはその確認の自動化への大きな前進とみなされ、高く評価されて当然の業績だと思います。

#Julia言語 では整数の商と余りを求める割り算での商は

x ÷ y

と書けます。÷ はJulia対応環境では「\div タブ」で入力できます。div(x, y)でもよい。

これを convert(Int, round(x/y)) のように書くのはひどく損になります。シンプルに x ÷ y でよい。