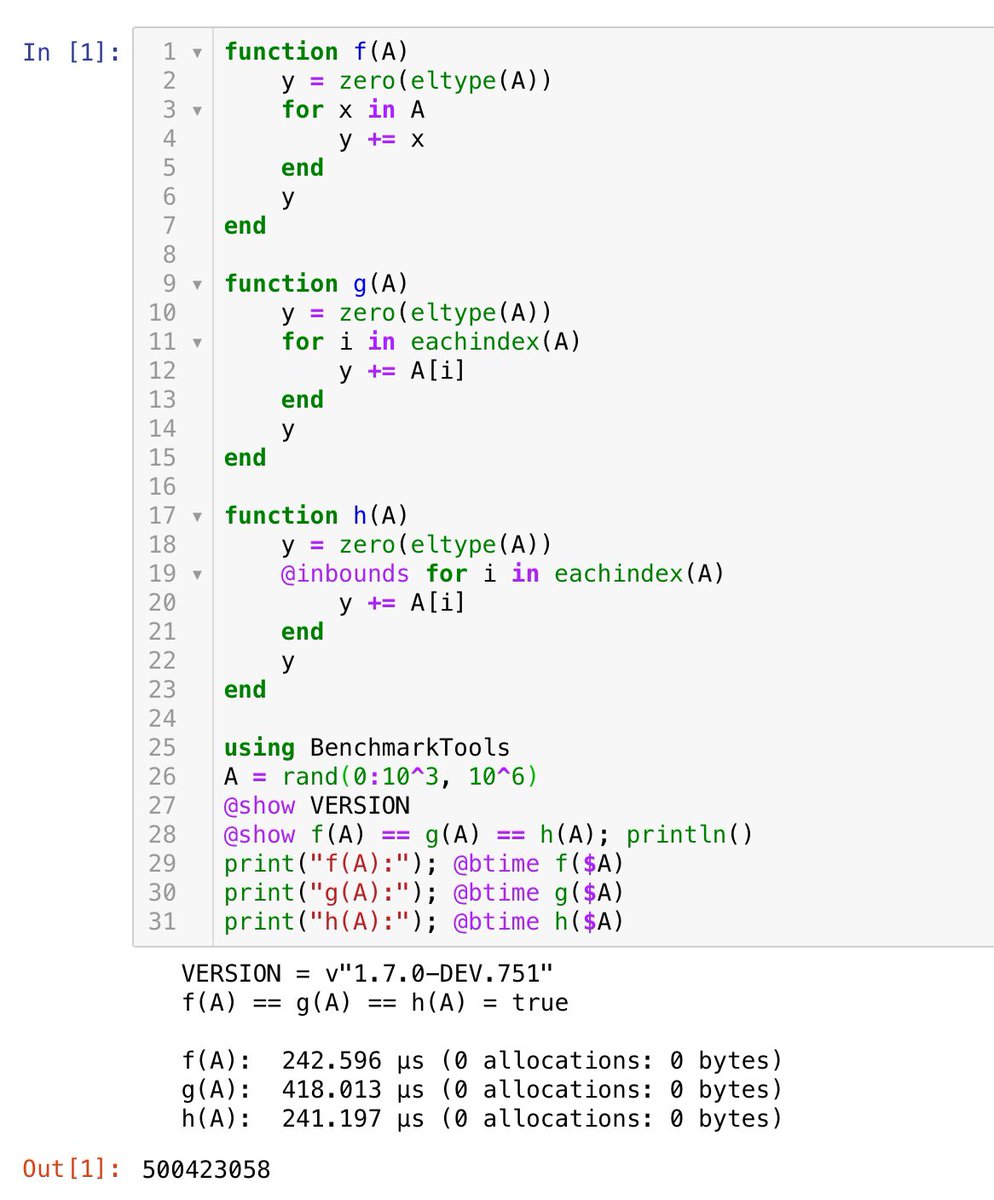
#Julia v1.6.0の公式バイナリが
julialang.org/downloads/
からダウンロード可能になっていて盛り上がっていますね。
新機能を2つ紹介
② sum系の函数で「初期値」を指定できるようになった。空の和もエラーにならないようにできます。
sum(x^3 for x in 1:0; init=0)
→0
これ結構重要。
julialang.org/downloads/
からダウンロード可能になっていて盛り上がっていますね。
新機能を2つ紹介
② sum系の函数で「初期値」を指定できるようになった。空の和もエラーにならないようにできます。
sum(x^3 for x in 1:0; init=0)
→0
これ結構重要。

#Julia言語 v1.6.0
②マクロ版ではなく、函数版sprintfが
using Printf
Printf.format(Printf.format"%15.10f", π)
のように使えるようになりました。
これで実行時可変なフォーマットのprintfを容易に使えます。
②マクロ版ではなく、函数版sprintfが
using Printf
Printf.format(Printf.format"%15.10f", π)
のように使えるようになりました。
これで実行時可変なフォーマットのprintfを容易に使えます。

#Julia言語 Julia言語では、コンパイル時に与えられたフォーマット専用のコードを生成する爆速のマクロ版printfがデフォルトで使えていました。C版のprintf函数より速い。
しかし、フォーマットが固定されるので不便な場合がたまにありました。v1.6.0以降は使い分ければよいということになります。
しかし、フォーマットが固定されるので不便な場合がたまにありました。v1.6.0以降は使い分ければよいということになります。
• • •
Missing some Tweet in this thread? You can try to
force a refresh