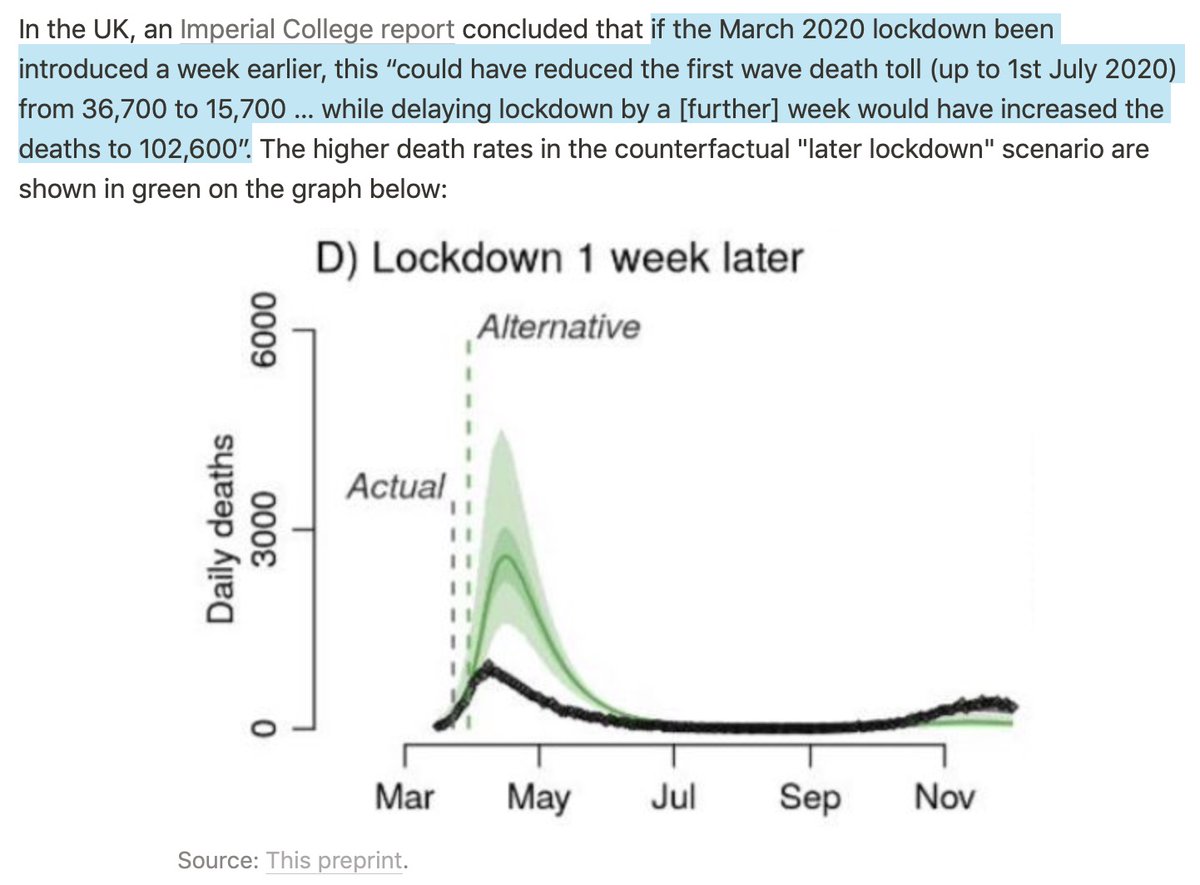
Epidemiologists claim that B.1.1.7 is far more transmissible than the historical lineage. In this post, I look at what happened in France and argue that, while B.1.1.7 initially had a large transmissibility advantage, it's been going down rapidly. (THREAD) cspicenter.org/blog/waronscie…
Various studies have estimated B.1.1.7's transmissibility advantage, but I focus on Gaymard et al. (2021), which found that it was between 50% and 70% more transmissible and has been used to calibrate official projections in France. eurosurveillance.org/content/10.280…
This estimate is based on fitting a simple exponential growth model to only 2 data points from January, during the early expansion of B.1.1.7 in France. This is problematic for several reasons and I won't get to the worst of them until the end of the thread, so stick with me.
First, in order to get an estimate of B.1.1.7's transmissibility advantage from this model, they need to make assumptions about the distribution of the generation time, i. e. the time between the moment someone is infected and the moment they infect someone else.
They assume this distribution has a mean of 6.5 days and a standard deviation of 4 days. (They also try with a mean of 5.5 days and a standard deviation of 1.8 days as a sensitivity analysis.) One problem is that it's higher than most estimates, but that's not the worst problem.
The worst problem is that we have no idea what the generation time distribution is right now in France. Very few estimates have been published, they're all over the place (with a mean ranging from 2.82 to 5.5 days) and the vast majority of them are based on early Chinese data.
Not only does the wide range of values in published estimates implies there is a lot of uncertainty about what the generation time distribution was at the beginning of the pandemic, but as I argue in the post, we have good reasons to think it's much shorter in France right now.
So I think the only epistemically responsible thing to do in order to estimate B.1.1.7's transmissibility advantage is to try a lot of possible values for the parameters of the generation time distribution and see how it affects the estimate.
As it turns out, the assumptions you make about the generation time distribution have a *huge* impact on the estimate of B.1.1.7's transmissibility advantage. 
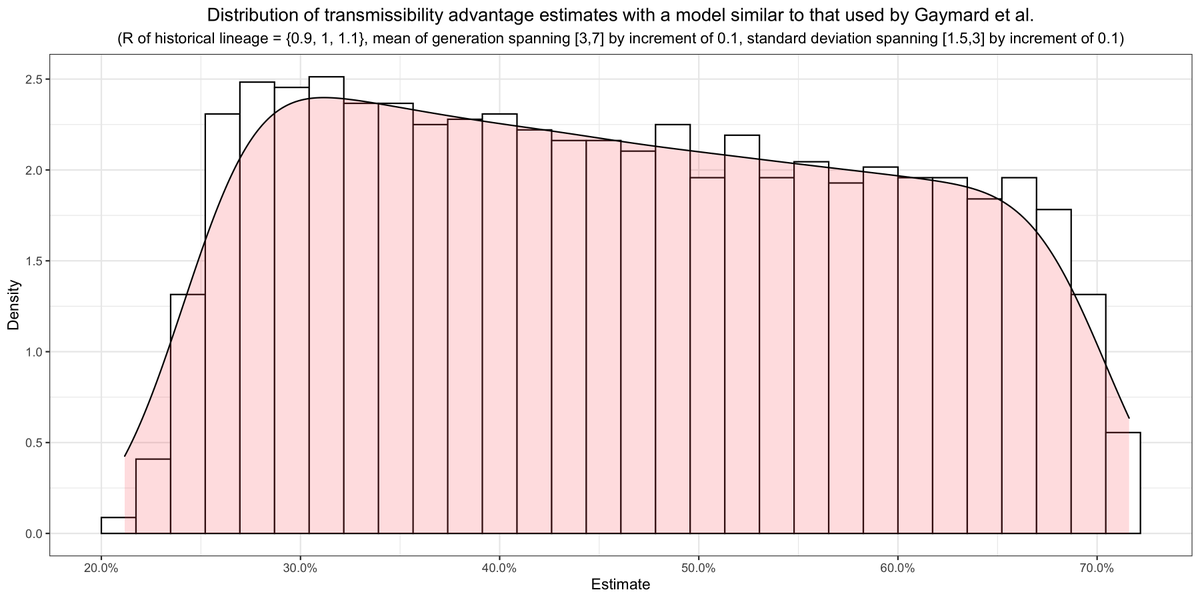
This figure shows the distribution of the estimates you get by fitting 1968 different specifications of Gaymard et al.'s model spanning a wide space of parameters. The estimates of B.1.1.7's transmissibility advantage range from 21% to 72%.
This is much wider than the 50%-70% range that Gaymard et al. report in their paper. When I use a meta-analytic estimate of the generation time distribution, I find a point estimate of 44%, much lower than Gaymard et al.'s central estimate of 59%.
However, I caution against taking that meta-analytic estimate very seriously, because as I mentioned above and argue more at length in the post it's based on data that we have good reasons to think are very misleading about the generation time distribution in France right now.
By the way, I say that I fitted different specifications of Gaymard et al.'s model but really I fitted different specifications of a similar model I wrote myself, because they didn't publish their code and the corresponding author didn't reply to me when I emailed him about it 🤷♂️
Anyway, those are the estimates of B.1.1.7's transmissibility advantage you get when you fit a simple exponential growth model to just 2 data points about the expansion of B.1.1.7 in January, but we now have a lot more data.
What happens if you fit the same kind of model on more recent data? Here is the distribution of estimates you get by doing the same kind of analysis as before. 
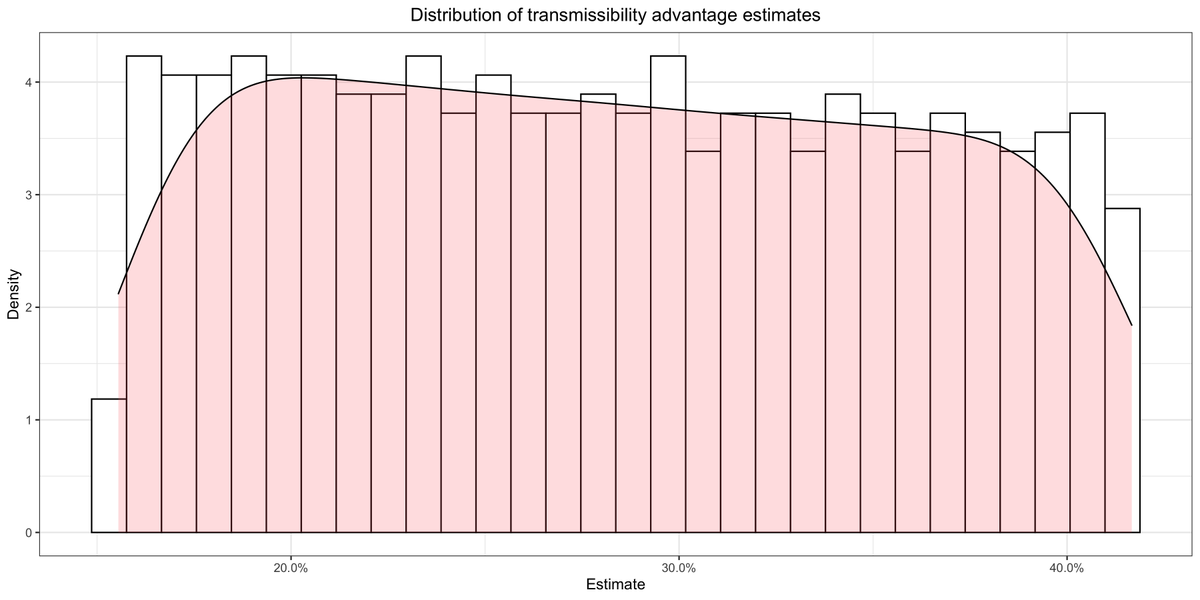
Using the meta-analytic estimate of the generation time distribution, B.1.1.7's transmissibility advantage is estimated at 27%, while over the whole parameter space it ranges from 16% to 42%. Again this is much lower than Gaymard et al.'s 50% to 70%.
However, although some epidemiologists inexplicably continue to insist that B.1.1.7 has been growing exponentially in France since the beginning of the year, it's clearly not the case and therefore we should not use a simple exponential growth model. 

As you can see, the R of B.1.1.7 has been going down a lot in France since the beginning of the year, so a simple exponential growth model is not realistic.
In fact, if B.1.1.7 had continued to grow at the same rate as in January (I made the same assumptions as Gaymard et al. to create this chart), there would be more than 500,000 cases a day by now, which is clearly not what happened. 
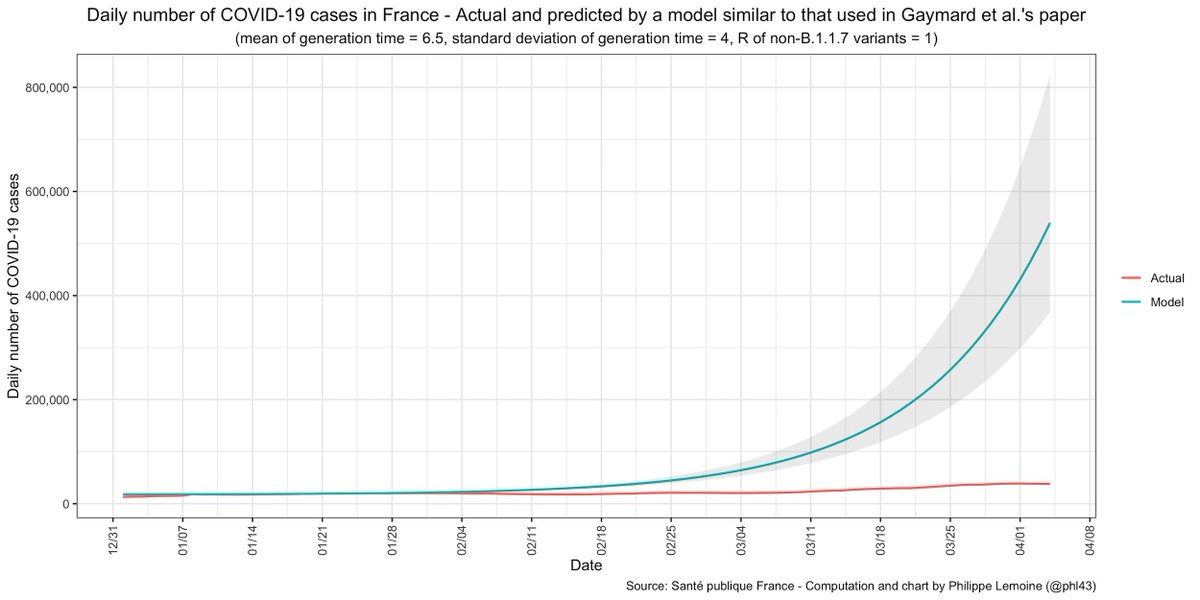
As long as the R of the other variants similarly went down, it could be that B.1.1.7's transmissibility advantage has remained the same though, which is what most epidemiologists assume.
For instance, in this paper (whose results were presented during a press conference of the government), the authors use a model that assumes B.1.1.7's transmissibility advantage is constant and ascribes this reduction of R to a curfew and school holidays. medrxiv.org/content/10.110…
The corresponding author also ignored me when I asked for the code, keep in mind those people are paid with my taxes, but I was able to come up with a similar model and it reached a similar conclusion. 
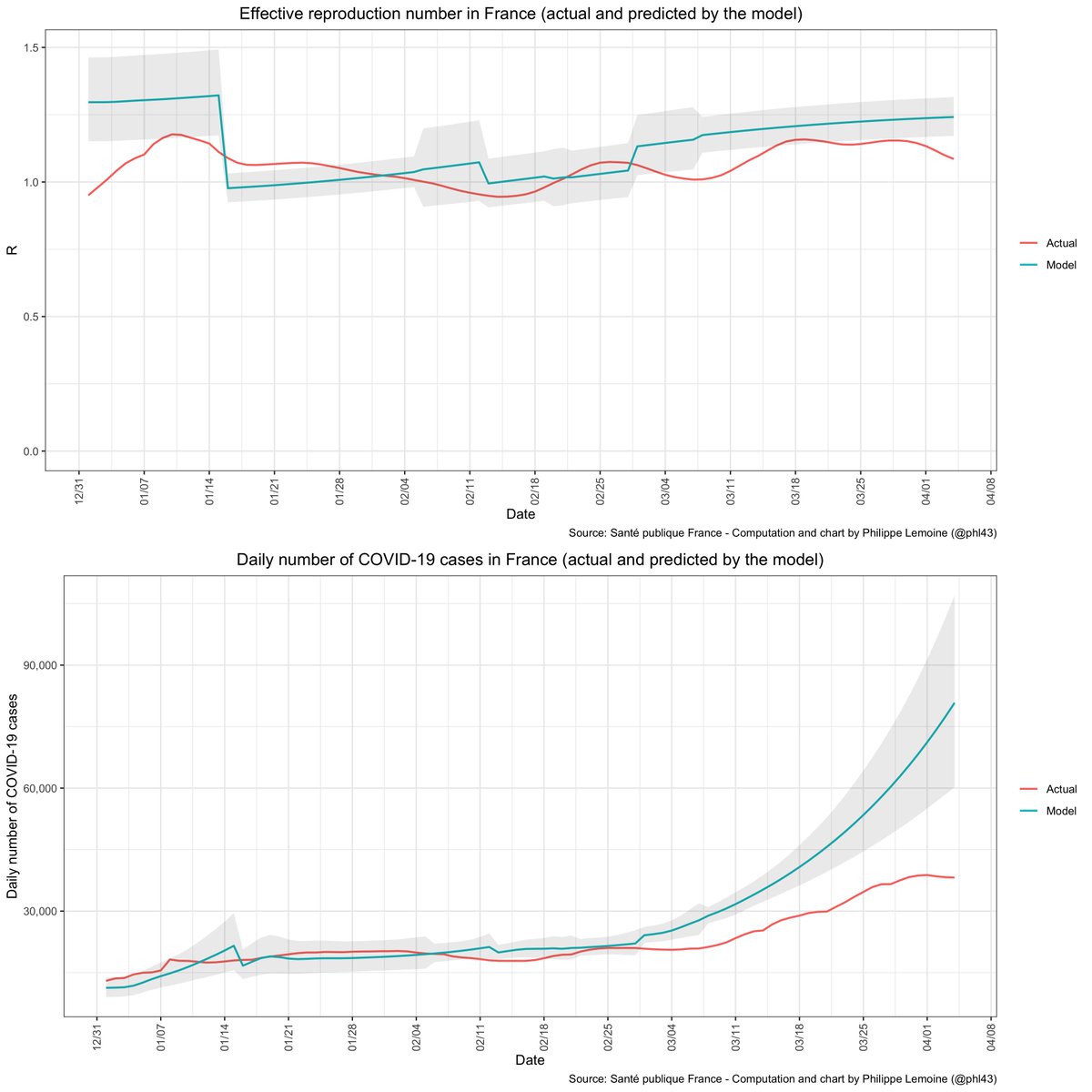
When I use the meta-analytical estimate of the generation time distribution, the model estimates B.1.1.7's transmissibility advantage at 35%. It's between 22% and 53% when you span the same parameter space as before. Again it's much lower than Gaymard et al.'s 50%-70% range.
It didn't matter to the authors of that paper though, since instead of using the model to estimate B.1.1.7's transmissibility advantage, they just plugged Gaymard et al.'s 60% estimate into it and used that to produce scary projections that were used to argue for a lockdown 👌
Anyway, even if B.1.1.7's transmissibility is only 35%, the model finds that incidence would have exploded if advancing the curfew from 8pm to 6pm in January had not reduced R across the board by 25% and the school holidays in February by 10%.
Of course, this never happened, the model just says it did because in fact the explosion didn't occur so it has to ascribe the reduction of R to *something* and it's set up in such a way that it has nothing else beside the curfew and the school holidays to ascribe it to 🙃
This is the kind of results that epidemiologists present with a straight face, but it's a complete joke since the conclusion is already baked into the assumptions of the model, as I already explained in my critique of Flaxman et al. (2020). necpluribusimpar.net/lockdowns-scie…
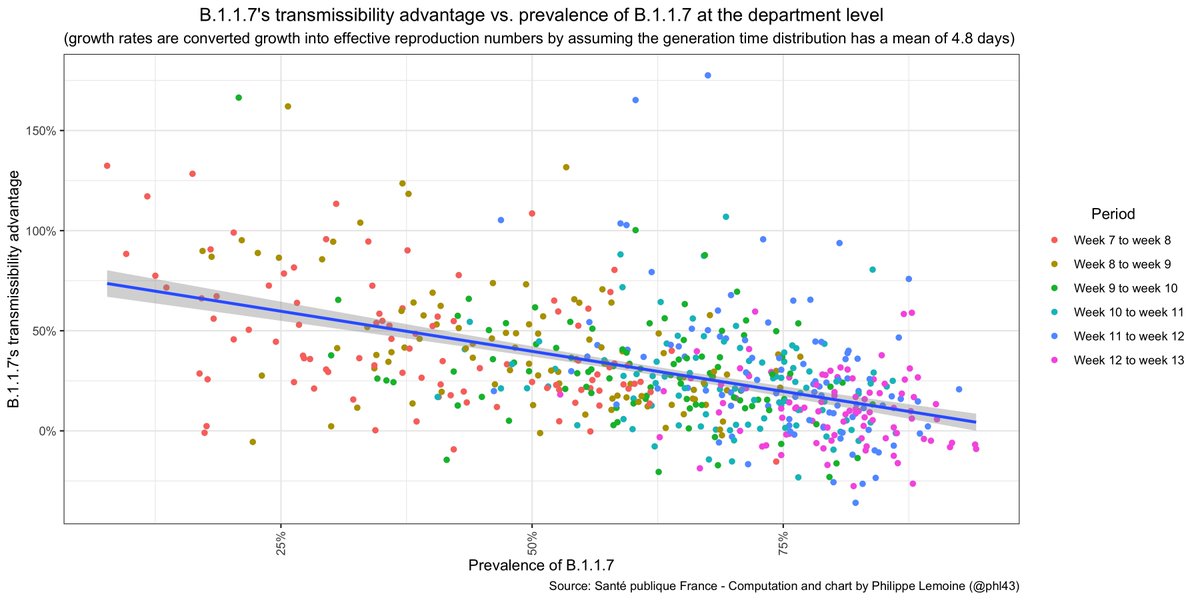
We can also use a more agnostic econometric approach to estimate B.1.1.7's transmissibility advantage. Instead of making strong mechanistic assumptions about transmission, we look at the correlation between the prevalence of B.1.1.7 and R.
If you just naively plot R against the prevalence of B.1.1.7 at the department level, it does look like a higher proportion of B.1.1.7 is associated with a higher reproduction number, although the effect is hardly impressive. 

However, for all sorts of reason, this could easily be misleading. For instance, if both R and the % of B.1.1.7 increase with time, even though the former is not a consequence of the latter. Disaggregating by week suggests that something like this might in fact be going on. 
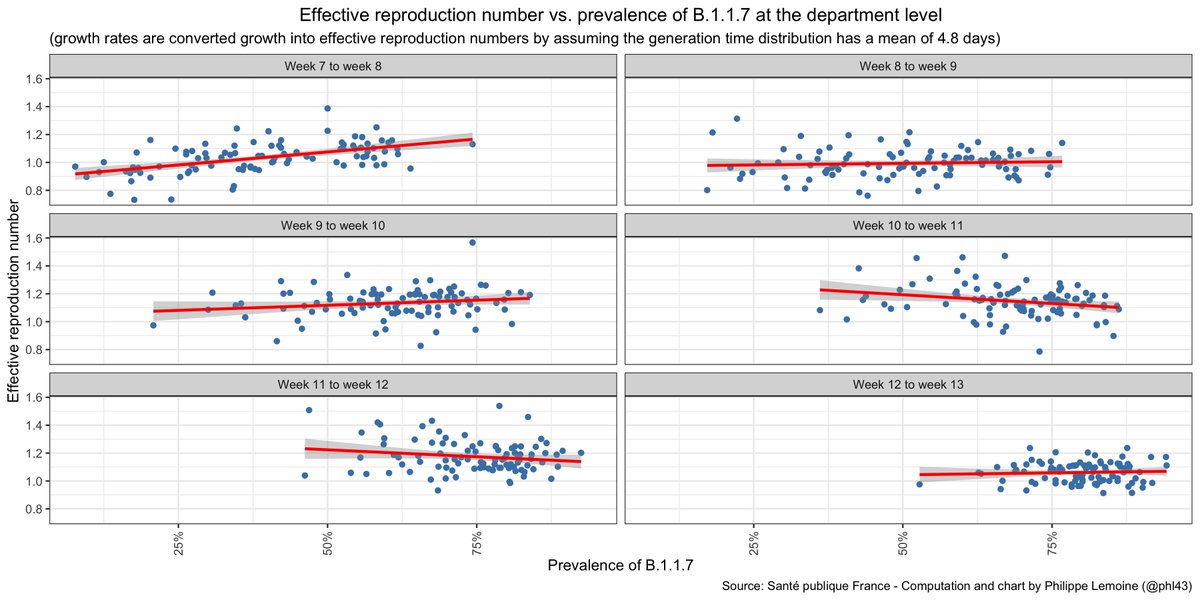
In order to sort this out, we can try a model with period and department fixed effect, but as I briefly explain in the post this comes with its own set of problems and it's not clear what is the best model, so I tried a bunch of them and here are the results. 
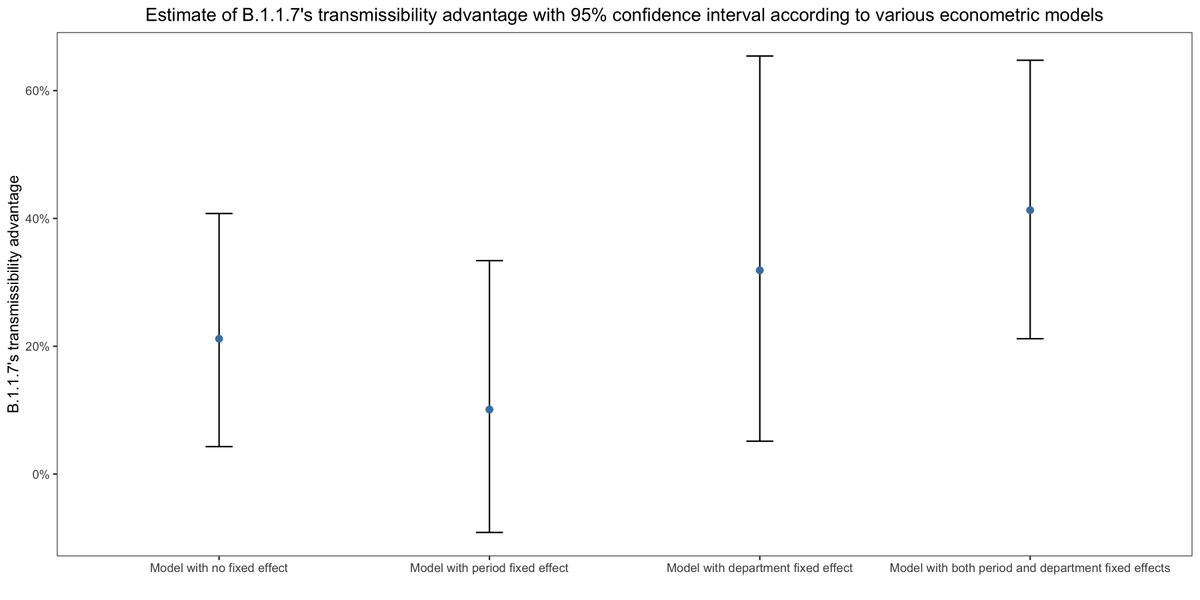
We still need to make assumptions about the generation time distribution to convert growth rates into reproduction numbers though. When I use the meta-analytical estimate, I find that B.1.1.7's transmissibility advantage is between 10% and 41% depending on what model I use.
However, the transmissibility advantage is very imprecisely estimated and, if you look at the confidence intervals, B.1.1.7 could be anywhere between 9% less transmissible and 65% more transmissible depending on the model we use.
When I make the same assumption as Gaymard et al. about the mean of the generation time distribution, the point estimates range from 14% to 60% and the confidence intervals put B.1.1.7's transmissibility advantage somewhere between -12% and 98% depending on the model.
In short, based on the econometric approach, we have no idea what B.1.1.7’s transmissibility advantage is. Estimates are so all over the place that we can’t even rule out that B.1.1.7 is *less* transmissible than the historical lineage.
Meanwhile, we have seen that when you try to estimate it by modeling transmission, the range of estimates is also very wide though generally much lower than Gaymard et al.’s 50%-70% range when using up to date data instead of just 2 data points from January.
So you’d think that epidemiologists would not take that 50%-70% estimate at face value and plug it into the models they use to make their projections, which are then presented to decision-makers, but you would be wrong because that’s exactly what they do...
Now, this is already bad, but that's not even the worst part. Not only do the various approaches I have reviewed so far don’t vindicate Gaymard et al.’s 50% to 70% estimate, but they’re all based on the assumption that B.1.1.7’s transmissibility advantage has remained constant.
Has it remained constant though? You would think that epidemiologists would be interested in that question, but apparently they couldn't be bothered to check. They just assumed it was, fitted a ridiculous model on 2 data points from January and plugged the result in their models!
Yet it's easy to check that B.1.1.7's transmissibility advantage has *not* remained constant in France since the beginning of the year. It has totally collapsed as the lineage expanded. I estimate that it's now only ~11% more transmissible than the other variants... 

The precise results depend on the assumption you make about the generation time, I used the same meta-analytical estimate as before but as I already noted we have no reason to think it's very good, but the qualitative conclusion is the same no matter what assumptions you make.
You see the same thing when you look at the data at the department level instead of aggregating at the national level. Incidence is also very high in France and we have lots of cases both for B.1.1.7 and the other variants, so this is not a sampling artifact or whatever. 
This explains why, even when we assume that B.1.1.7's transmissibility advantage has remained constant but use all the data up to today instead of just 2 data points from January, we generally find that it's much lower than Gaymard et al.'s 50%-70% estimate.
Indeed, by doing that, we're telling our models that B.1.1.7's transmissibility has remained constant but feeding it data from a process in which it has been going down over time, so it's going to estimate a transmissibility advantage somewhere in the middle.
I have only looked at French data, but as @ClimateAudit noted, British epidemiologists have apparently uncovered a similar pattern of B.1.1.7's transmissibility advantage going down over time, although they aren't in a hurry to advertise this discovery.
https://twitter.com/ClimateAudit/status/1366045932652032005
It's not easy to figure out what the underlying mechanism for this phenomenon could be. The data looks like there is some kind of direct competition between the variants, but I don't think there is any plausible mechanism for that.
People have proposed various hypotheses that could explain that, but I find most of them unsatisfactory. My favorite so far is @WesPegden's hypothesis that B.1.1.7 has a different susceptibility profile than the historical lineage.
https://twitter.com/WesPegden/status/1346298493162450944
In any case, trying to figure out what the mechanism could be is exactly what epidemiologists should be doing right now, but unfortunately they don't seem to be very interested in that...
They seem more interested in whipping up hysteria about impending doom caused by this variant and severely misrepresent the real uncertainty when they talk to the media about that issue.
It's totally unacceptable to take a very high estimate based on fitting a ridiculous model to 2 data points from January and plug that into the models used to make projections, even though it's clear in the data that B.1.1.7's transmissibility advantage has collapsed since then.
It's even worse when, instead of acknowledging that your models were mistaken, you stick to your guns and make up purely ad hoc explanations to argue that even though your predictions didn't come true you were still totally right, which is what French epidemiologists have done.
As I explain in the post, this is easy to do because epidemiological models are very flexible and you can always come up with one that will allow you to tell whatever story you want to tell, but this is not intellectually honest.
The fundamental problem here is that models based on flawed assumptions have taken a life of their own and nobody is checking them against the data in a scientifically responsible manner. It's hard not to think that it's because they result in the "right" policy recommendations.
Epidemiologists have a responsibility to stop doing that, not just because not doing so could result in costly policy mistakes during the pandemic, but also because if they don't it will eventually discredit not just epidemiological modeling but scientific modeling in general.
Of course, not all epidemiologists have been doing that, but I think most of them have because incentives are messed up and encourage people to underestimate true uncertainty and make apocalyptic predictions.
Anyway, I hope this thread will have convinced you that things are more complicated than it seems, please read the post and share it if you found it interesting.
P. S. To be clear, I don't believe it's actually less transmissible. The explanation for this surprising result is likely that B.1.1.7's transmissibility advantage has been going down over time, so the model is misspecified, as I explain later in thread.
https://twitter.com/phl43/status/1380515957278437379
P. S. bis: It's another hypothesis but I don't think this kind of founder effect is very likely, because if that were the explanation, B.1.1.7 wouldn't have quickly taken over everywhere it was introduced, especially in places where incidence was high.
https://twitter.com/prtsnf/status/1380525120779866117
P. S. ter: If something like @WesPegden's hypothesis is correct, I think we'd expect B.1.1.7's transmissibility advantage to go down less rapidly in places where the lineage took over while incidence was low, so this might be another way to test this hypothesis.
P. S. quater: This is a very good and important question in my opinion. I briefly argue at the end of the post that the answer is "not really" and I think it's something people should think about more.
https://twitter.com/GatesPendleton/status/1380539094086819848
Oops, I realize that I didn't share the right graph above to show that B.1.1.7's transmissibility advantage hasn't remained constant, here is the right one. 
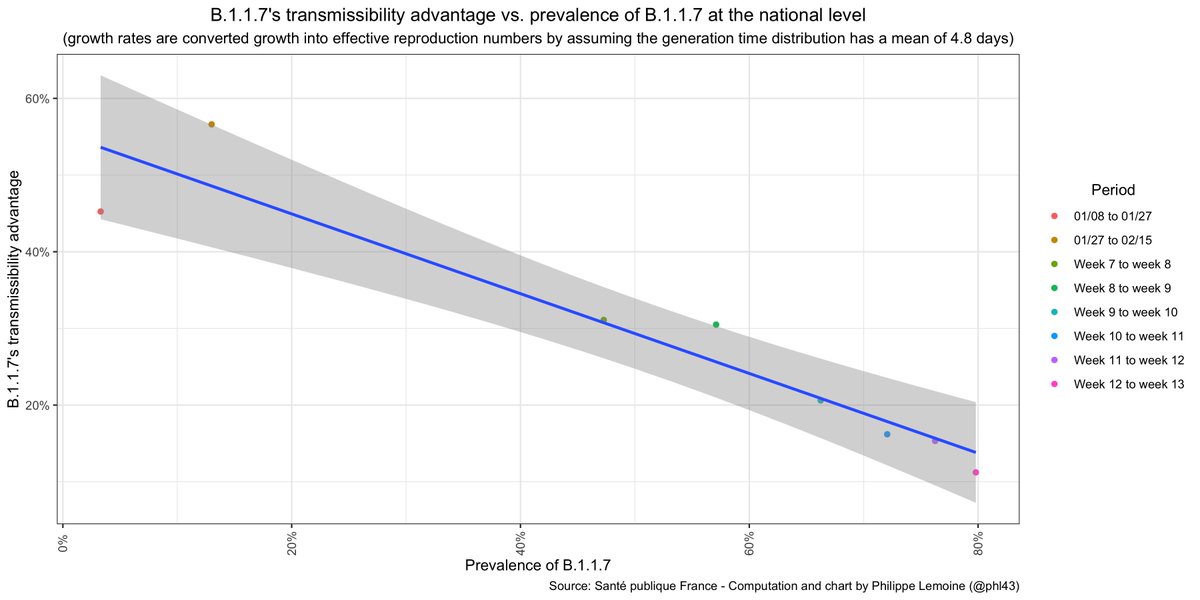
• • •
Missing some Tweet in this thread? You can try to
force a refresh