1/
Get a cup of coffee.
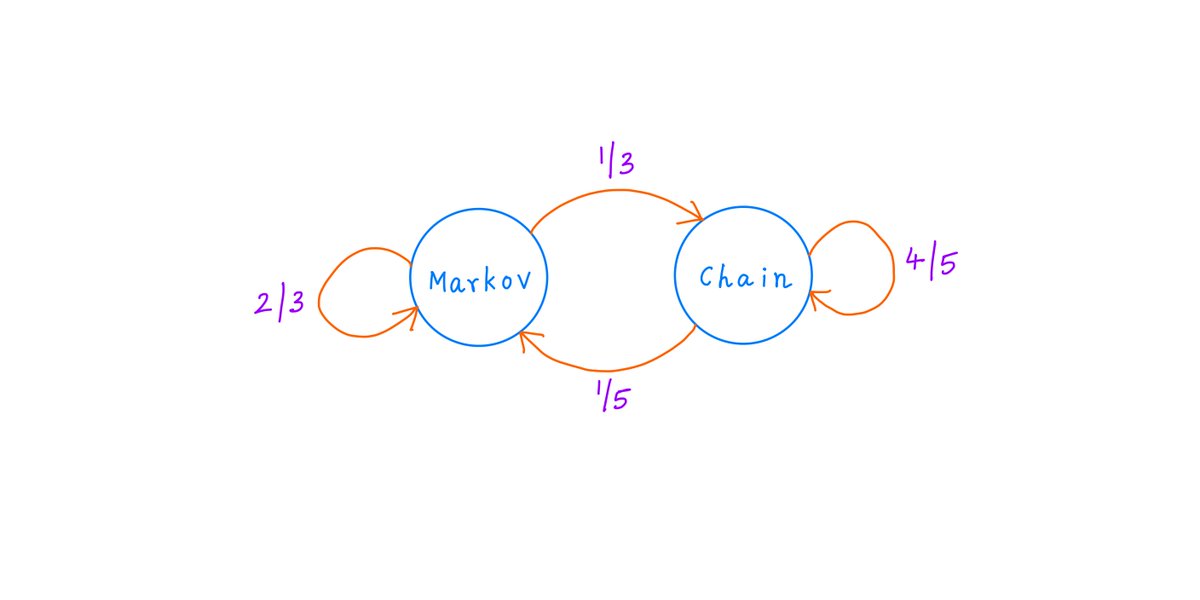
In this thread, I'll help you understand Markov Chains.
In life, and in investing, we often come across situations where luck/chance plays a major role.
And Markov Chains are often a great way to model and analyze such situations.
Get a cup of coffee.
In this thread, I'll help you understand Markov Chains.
In life, and in investing, we often come across situations where luck/chance plays a major role.
And Markov Chains are often a great way to model and analyze such situations.
2/
Here's what prompted me to write this thread.
Earlier this week, I conducted a Twitter poll.
In the poll, I posed a question that required a bit of probabilistic reasoning.
The good news: over 10,000 people responded.
The bad news: ~87% got the answer wrong!
Here's what prompted me to write this thread.
Earlier this week, I conducted a Twitter poll.
In the poll, I posed a question that required a bit of probabilistic reasoning.
The good news: over 10,000 people responded.
The bad news: ~87% got the answer wrong!
3/
Here's the question I asked.
Imagine we have 2 volunteers: Alice and Bob.
We give them each a fair coin.
We ask Alice to keep tossing her coin until she sees a Heads immediately followed by a Tails (ie, the pattern HT).
Here's the question I asked.
Imagine we have 2 volunteers: Alice and Bob.
We give them each a fair coin.
We ask Alice to keep tossing her coin until she sees a Heads immediately followed by a Tails (ie, the pattern HT).
4/
We ask Bob to keep tossing his coin until he sees two consecutive Heads (ie, the pattern HH).
The question is: on average, who will take more tosses to get to their "target pattern" -- Alice or Bob?
Or will they both on average take the same number of tosses?
We ask Bob to keep tossing his coin until he sees two consecutive Heads (ie, the pattern HH).
The question is: on average, who will take more tosses to get to their "target pattern" -- Alice or Bob?
Or will they both on average take the same number of tosses?
5/
More precisely:
Suppose Alice takes A tosses on average to get her HT.
And Bob takes B tosses on average to get his HH.
Then, which is the bigger number: A or B?
Or are they both the same number?
More precisely:
Suppose Alice takes A tosses on average to get her HT.
And Bob takes B tosses on average to get his HH.
Then, which is the bigger number: A or B?
Or are they both the same number?
6/
We know Alice and Bob both have fair coins.
So, in any 2 consecutive tosses, Alice's HT is just as likely to show up as Bob's HH.
So, on average, it *seems* like they'll both take the same number of tosses (ie, A = B).
We know Alice and Bob both have fair coins.
So, in any 2 consecutive tosses, Alice's HT is just as likely to show up as Bob's HH.
So, on average, it *seems* like they'll both take the same number of tosses (ie, A = B).
7/
In fact, that's exactly what ~77% of poll respondents said:
In fact, that's exactly what ~77% of poll respondents said:
https://twitter.com/10kdiver/status/1382086546161995778?s=20
8/
But that's *not* the right answer.
The right answer is: on average, Alice's HT will appear in just 4 tosses.
But Bob's HH will take 6 tosses.
That is, A = 4 and B = 6.
Bob, on average, takes longer.
How strange!
But that's *not* the right answer.
The right answer is: on average, Alice's HT will appear in just 4 tosses.
But Bob's HH will take 6 tosses.
That is, A = 4 and B = 6.
Bob, on average, takes longer.
How strange!
9/
Here's the thing:
When it comes to probability, our intuition often leads us astray.
The best way to deal with it is to meticulously write down the various possible outcomes and actually work through the math.
And Markov Chains are handy models for doing just that.
Here's the thing:
When it comes to probability, our intuition often leads us astray.
The best way to deal with it is to meticulously write down the various possible outcomes and actually work through the math.
And Markov Chains are handy models for doing just that.
10/
For example, here is Alice's Markov Chain.
It shows that, at any time, Alice can be in one of 4 possible "states" (S0 through S3).
At each state, Alice tosses her coin.
And depending on the outcome of the toss (H or T), she moves to a different state if needed.
For example, here is Alice's Markov Chain.
It shows that, at any time, Alice can be in one of 4 possible "states" (S0 through S3).
At each state, Alice tosses her coin.
And depending on the outcome of the toss (H or T), she moves to a different state if needed.

11/
For example, S0 is the "start" state. It's where Alice starts her journey.
At S0, Alice tosses her coin.
If it comes up Heads, she follows the orange arrow from S0 (labeled "H"), which takes her to S1.
For example, S0 is the "start" state. It's where Alice starts her journey.
At S0, Alice tosses her coin.
If it comes up Heads, she follows the orange arrow from S0 (labeled "H"), which takes her to S1.
12/
At S1, Alice has seen a Heads, and is hoping for a Tails next (so she has her HT pattern).
If her toss at S1 comes up Tails, she goes to S2 -- her Win state; HT secured.
But if it comes up Heads instead, she follows the orange arrow from S1, which keeps her at S1 itself.
At S1, Alice has seen a Heads, and is hoping for a Tails next (so she has her HT pattern).
If her toss at S1 comes up Tails, she goes to S2 -- her Win state; HT secured.
But if it comes up Heads instead, she follows the orange arrow from S1, which keeps her at S1 itself.
13/
That's all a Markov Chain is.
There's a bunch of states. At each state, a random event (like a coin toss) happens.
Based on the outcome of this random event, we follow the appropriate arrow to go to the next state.
Once at the next state, we rinse and repeat.
That's all a Markov Chain is.
There's a bunch of states. At each state, a random event (like a coin toss) happens.
Based on the outcome of this random event, we follow the appropriate arrow to go to the next state.
Once at the next state, we rinse and repeat.
14/
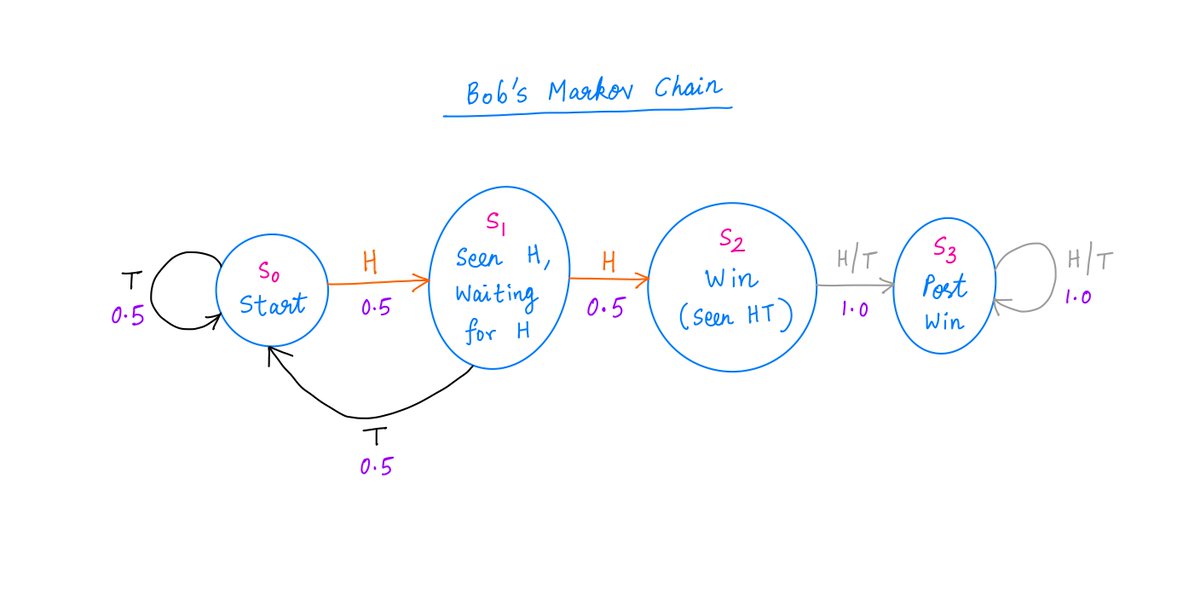
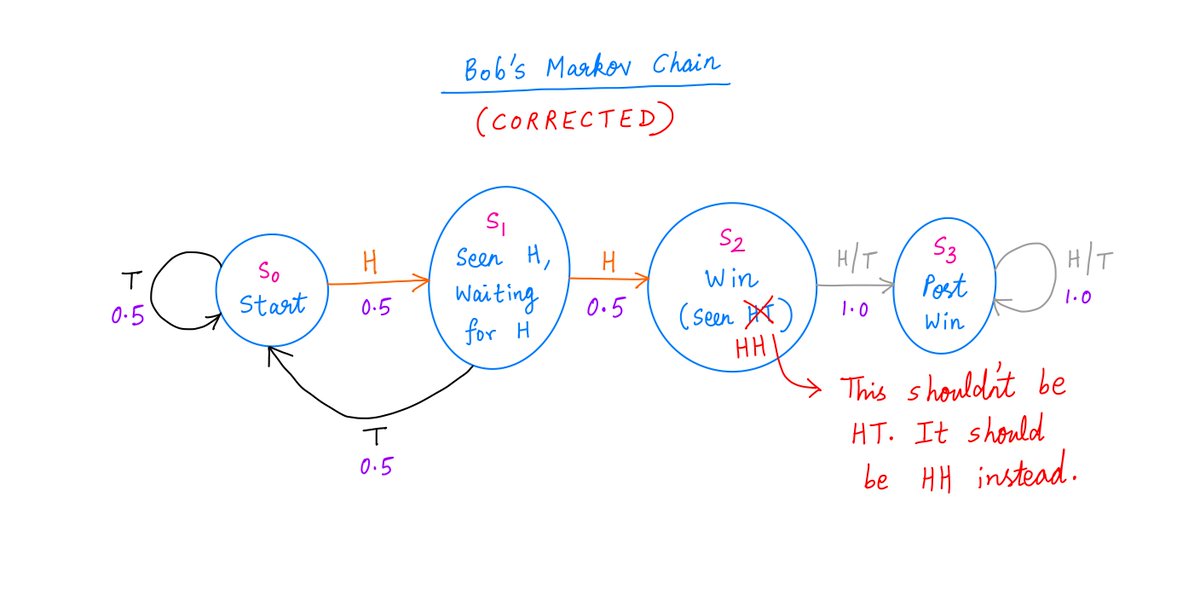
Here's Bob's Markov Chain.
The difference between Alice and Bob is now clear.
When Bob is at S1 and gets unlucky (with a T), he has to "go back to zero" (S0) and start over.
Not so for Alice. Once Alice is at S1, she never ever has to go back to S0.
Here's Bob's Markov Chain.
The difference between Alice and Bob is now clear.
When Bob is at S1 and gets unlucky (with a T), he has to "go back to zero" (S0) and start over.
Not so for Alice. Once Alice is at S1, she never ever has to go back to S0.
15/
That's why Bob takes longer!
From time to time, unlike Alice, Bob is forced to start from zero all over again. That's a drag.
Alice is like a drunk who either stays put or marches forward.
But Bob is like a drunk who also stumbles *backwards* on occasion.
That's why Bob takes longer!
From time to time, unlike Alice, Bob is forced to start from zero all over again. That's a drag.
Alice is like a drunk who either stays put or marches forward.
But Bob is like a drunk who also stumbles *backwards* on occasion.
16/
The nice thing about Markov Chains is that they allow us to quantify all this.
If we know the initial state (S0 for both Alice and Bob), we can calculate the probability of being in *any* state at *any* time.
There's a simple formula for this.
The nice thing about Markov Chains is that they allow us to quantify all this.
If we know the initial state (S0 for both Alice and Bob), we can calculate the probability of being in *any* state at *any* time.
There's a simple formula for this.
17/
This formula is "iterative".
That is, if we know the probability of being in each state at time "k" (ie, after "k" coin tosses), the formula gives us the probability of each state at the *next* time "k+1" (ie, after "k+1" coin tosses).
This formula is "iterative".
That is, if we know the probability of being in each state at time "k" (ie, after "k" coin tosses), the formula gives us the probability of each state at the *next* time "k+1" (ie, after "k+1" coin tosses).
18/
It's quite simple.
We take the probabilities at time "k", and we pre-multiply them by a matrix (known as the Markov matrix or the Transition matrix).
This multiplication gives us the probabilities at time "k+1".
Like so:
It's quite simple.
We take the probabilities at time "k", and we pre-multiply them by a matrix (known as the Markov matrix or the Transition matrix).
This multiplication gives us the probabilities at time "k+1".
Like so:
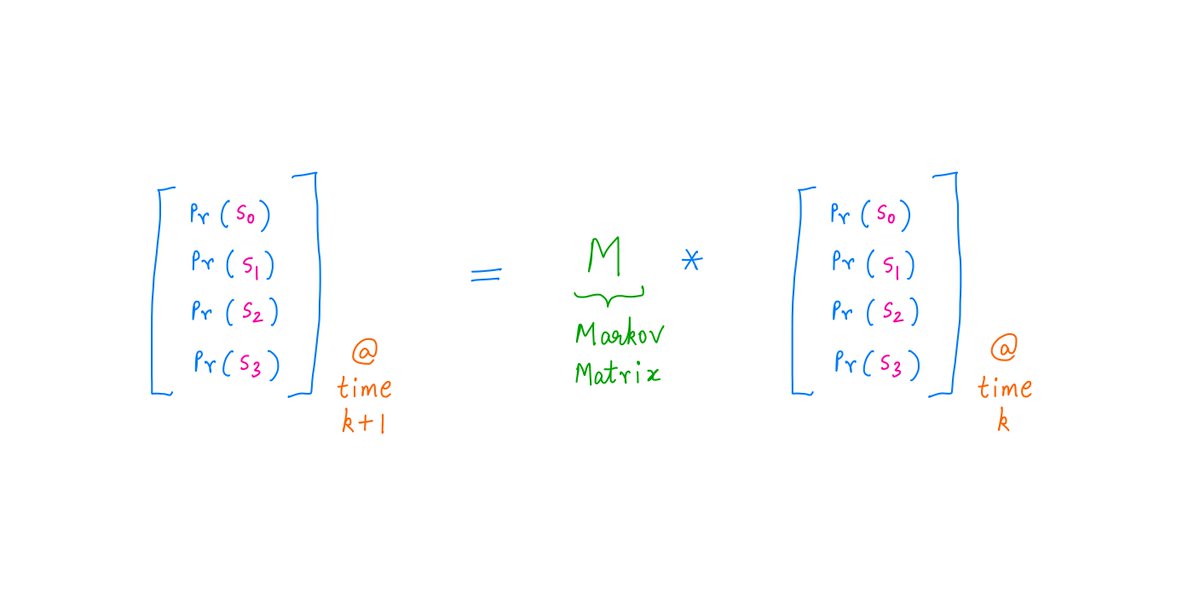
19/
Here are the Markov matrices for Alice and Bob.
To get these matrices, we simply take the probability of each Markov Chain "arrow", and place it in the appropriate matrix slot according to the arrow's "From" and "To" states.
Here are the Markov matrices for Alice and Bob.
To get these matrices, we simply take the probability of each Markov Chain "arrow", and place it in the appropriate matrix slot according to the arrow's "From" and "To" states.

20/
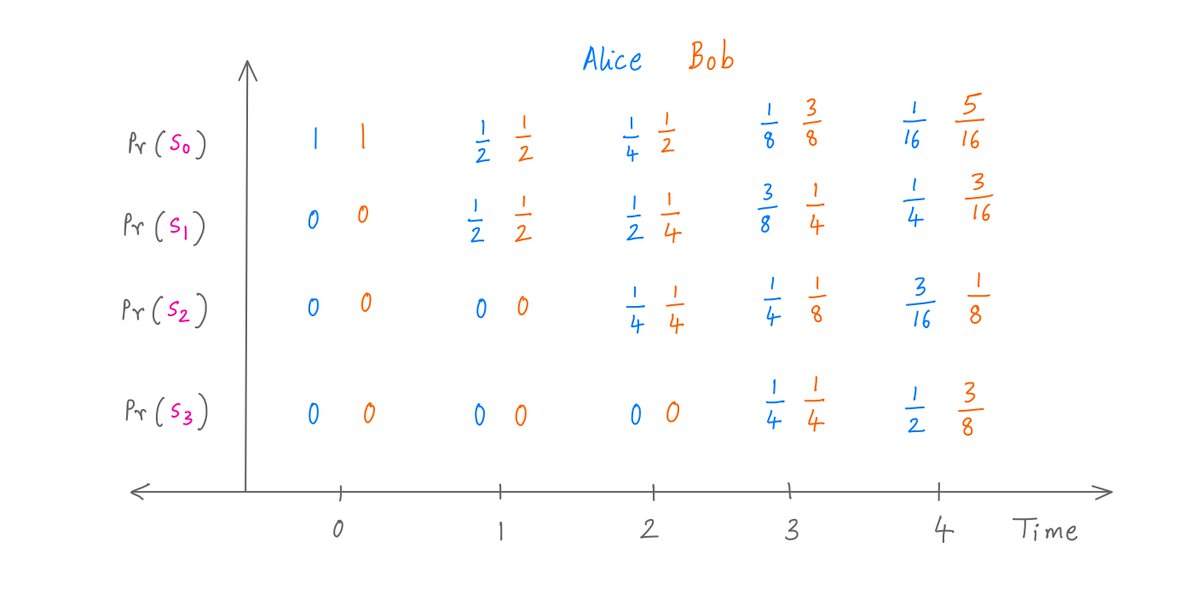
Now, we can iterate.
Using repeated Markov matrix pre-multiplications, we get the probability of Alice and Bob being in every possible state at every possible time.
Like so (for times 0 through 4):
Now, we can iterate.
Using repeated Markov matrix pre-multiplications, we get the probability of Alice and Bob being in every possible state at every possible time.
Like so (for times 0 through 4):
21/
At any time, if Alice or Bob has seen their target pattern, they'd be in S2 or S3.
So, we can see that after 4 coin tosses, Alice already has a Pr(S2) + Pr(S3) = 3/16 + 1/2 = 68.75% chance of being done.
But Bob only has a 50% chance of being done by that time.
At any time, if Alice or Bob has seen their target pattern, they'd be in S2 or S3.
So, we can see that after 4 coin tosses, Alice already has a Pr(S2) + Pr(S3) = 3/16 + 1/2 = 68.75% chance of being done.
But Bob only has a 50% chance of being done by that time.
22/
Getting the *average* time to completion is also not hard.
As "completion at, but not before, time k" is the same as "being in state S2 at time k", we have the following:
Getting the *average* time to completion is also not hard.
As "completion at, but not before, time k" is the same as "being in state S2 at time k", we have the following:

23/
So, that's the basic math of Markov Chains.
It's so simple. We move from state to state based on the outcome of chance events like coin flips.
And so powerful. Knowing just the initial state, we can exactly calculate the probability of being in *any* state at *any* time.
So, that's the basic math of Markov Chains.
It's so simple. We move from state to state based on the outcome of chance events like coin flips.
And so powerful. Knowing just the initial state, we can exactly calculate the probability of being in *any* state at *any* time.
24/
So, what lessons can we learn from this exercise?
Key lesson 1. Probability often challenges our intuition.
That's why ~87% of FinTwit got my poll question wrong.
They relied on *intuition* rather than *math*.
So, what lessons can we learn from this exercise?
Key lesson 1. Probability often challenges our intuition.
That's why ~87% of FinTwit got my poll question wrong.
They relied on *intuition* rather than *math*.
25/
But chance and uncertainty are everywhere in life.
So, it's important to learn how to reason correctly about probabilistic situations -- using systematic mathematical techniques, *without* relying on our intuition.
As Charlie Munger puts it:
But chance and uncertainty are everywhere in life.
So, it's important to learn how to reason correctly about probabilistic situations -- using systematic mathematical techniques, *without* relying on our intuition.
As Charlie Munger puts it:

26/
Key lesson 2. As far as possible, we should avoid putting ourselves in situations where a single turn of bad luck could force us to start over from zero.
This was Bob's problem. That's why he took longer than Alice in our example.
Key lesson 2. As far as possible, we should avoid putting ourselves in situations where a single turn of bad luck could force us to start over from zero.
This was Bob's problem. That's why he took longer than Alice in our example.
27/
In investing, the equivalent is using too much leverage, naked options, trading on margin, etc.
By doing these things, we put ourselves in a position where short-term volatility and chance events could wipe us out, forcing us to essentially start from zero all over again.
In investing, the equivalent is using too much leverage, naked options, trading on margin, etc.
By doing these things, we put ourselves in a position where short-term volatility and chance events could wipe us out, forcing us to essentially start from zero all over again.
28/
Key lesson 3. It's important to familiarize ourselves with "the classics" -- great ideas from multiple disciplines.
Markov Chains are not new; they date back to 1906.
But to this day, they're heavily used in various fields -- from engineering to biology.
Key lesson 3. It's important to familiarize ourselves with "the classics" -- great ideas from multiple disciplines.
Markov Chains are not new; they date back to 1906.
But to this day, they're heavily used in various fields -- from engineering to biology.
29/
Such classic ideas that have withstood the test of time are often worthy of study.
They frequently help us think more clearly -- and thereby understand the world better.
They're good candidates for adding to our "latticework of mental models", as Charlie Munger puts it.
Such classic ideas that have withstood the test of time are often worthy of study.
They frequently help us think more clearly -- and thereby understand the world better.
They're good candidates for adding to our "latticework of mental models", as Charlie Munger puts it.
30/
One last thought.
Remember the game "Snakes and Ladders"?
That's a Markov Chain.
Each square on the board is a "state" we can be in. We transition between states based on random events (in this case, die rolls).
Once we know a concept, we start seeing it everywhere!
One last thought.
Remember the game "Snakes and Ladders"?
That's a Markov Chain.
Each square on the board is a "state" we can be in. We transition between states based on random events (in this case, die rolls).
Once we know a concept, we start seeing it everywhere!
31/
Thank you very much for reading to the end of yet another long thread -- this one somewhat more mathematical than usual!
Please stay safe. Enjoy your weekend!
/End
Thank you very much for reading to the end of yet another long thread -- this one somewhat more mathematical than usual!
Please stay safe. Enjoy your weekend!
/End
ERROR:
In Tweet 14 above, I made a mistake in the picture showing Bob's Markov Chain.
The label on state S2 should have said "Seen HH", not "Seen HT". Corrected pic below.
Sorry about that! And many thanks to Rex Mayne (@r_mayne) for catching it and alerting me!
In Tweet 14 above, I made a mistake in the picture showing Bob's Markov Chain.
The label on state S2 should have said "Seen HH", not "Seen HT". Corrected pic below.
Sorry about that! And many thanks to Rex Mayne (@r_mayne) for catching it and alerting me!
• • •
Missing some Tweet in this thread? You can try to
force a refresh