Thread by @andrewgwils

What are Bayesian neural network posteriors really like? With high fidelity HMC, we study approximate inference quality, generalization, cold posteriors, priors, and more.
arxiv.org/abs/2104.14421
With @Pavel_Izmailov, @sharadvikram, and Matthew D. Hoffman. 1/10

We show that Bayesian neural networks reassuringly provide good generalization, outperforming deep ensembles, standard training, and many approximate inference procedures, even with a single chain. 2/10

However, we find that BNNs are surprisingly poor at OOD generalization, even worse than SGD, despite the popularity of approximate inference in this setting, and the relatively good performance of BNNs for OOD detection. 3/10

Even though deep ensembles are often talked about as a "non-Bayesian" alternative to standard approximate inference, we find they approximate the HMC predictive distribution better than MFVI, and about as well as standard SGLD. 4/10

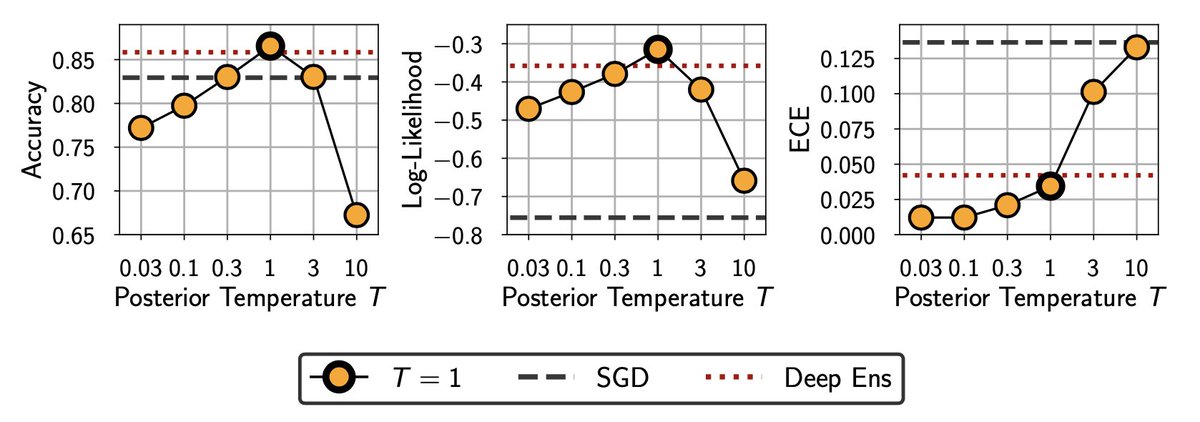
There has been much attention lately on "cold posteriors" in BDL, where the posterior raised to a power 1/T with T<1 can lead to better results. We see little evidence for a general cold posterior effect, which we find is largely due to data augmentation. 5/10

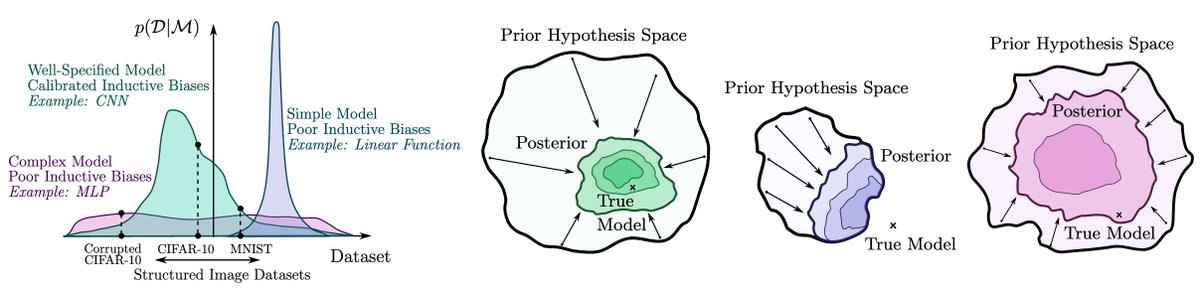
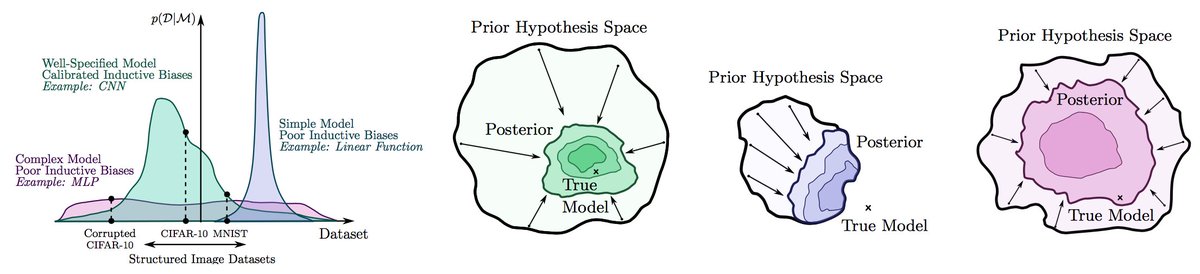
We explored Gaussian, mixture of Gaussian, and heavy-tailed logistic priors, which performed similarly, although the heavy-tailed priors did slightly better. We also found performance relatively insensitive to the scale of the Gaussian prior... 6/10

...these results highlight the relative importance of the architecture compared to the distribution over weights in defining the induced prior over functions. Indeed, other work shows that even standard Gaussian priors have many useful properties: arxiv.org/abs/2002.08791. 7/10

We present many other results, including mixing in function space vs. weight space, posterior geometry and mode connecting paths, single chain vs. multi-chain...! 8/10

Many of the results, both positive and negative for BDL, are contrary to conventional wisdom. 9/10

We worked hard to obtain these HMC samples, which we plan to release as a public resource, as a reference for evaluating more practical alternatives to HMC, and for researchers to explore their own questions around approximate inference in BDL. 10/10