Thread by @TivadarDanka

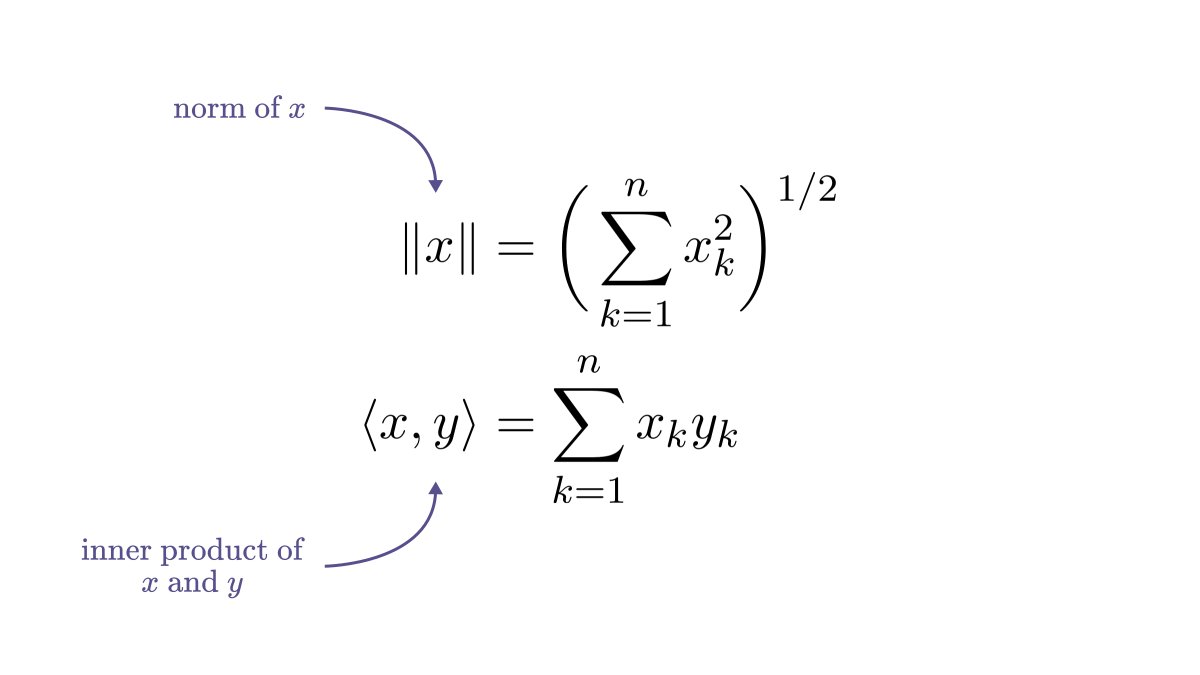
As you know, I am working on teaching mathematics in a way that maximizes value for machine learning practitioners.

Do you have any work stories where mathematical knowledge was a genuine advantage?

I would appreciate it if you could share!

I'll start. ↓

As a bioimage analyst, one of my projects involved the pixel-perfect identification of very thin objects: plant seedlings. (Like below.)

This was a classical semantic segmentation problem.

At first, I trained a UNet model using cross-entropy loss, but it didn't quite work.

The problem was that on the segmentation output, objects were not defined at all. My model predicted almost every pixel as background.

With some basic mathematical thinking, I suspected that the problem is caused by the cross-entropy loss.

See, if the vast majority of ground truth pixels belong to the background, cross-entropy loss is small when all pixels are actually predicted as background.

So, I started to look for loss functions that are more sensitive to rare classes.

Again, my mathematical intuition suggested that measuring something like the average overlap ratio per class should work.

Since I knew what I looking for, a quick research gave me what I needed: the Dice loss. (Cool article below if you are interested.)

medium.com/ai-salon/under…

With the Dice loss, my model started to work, and eventually, we solved the problem.

You can see the result below. This was the predicted class label map for one of our test images.

(Our work was published in an academic journal, check it out if you are interested. It is open access, so you can read it for free.)

academic.oup.com/plphys/article…

I have many stories like this, but now I would love to hear some from you!

Was math ever an advantage for you? Or you never really used it, always wondering why it is taught for machine learning practitioners?

Let me know!