Tweet

Tivadar Danka

5 Oct, 10 tweets, 4 min read

There is one big reason we love the logarithm function in machine learning.

Logarithms help us reduce complexity by turning multiplication into addition. You might not know it, but they are behind a lot of things in machine learning.

Here is the entire story.

🧵 👇🏽

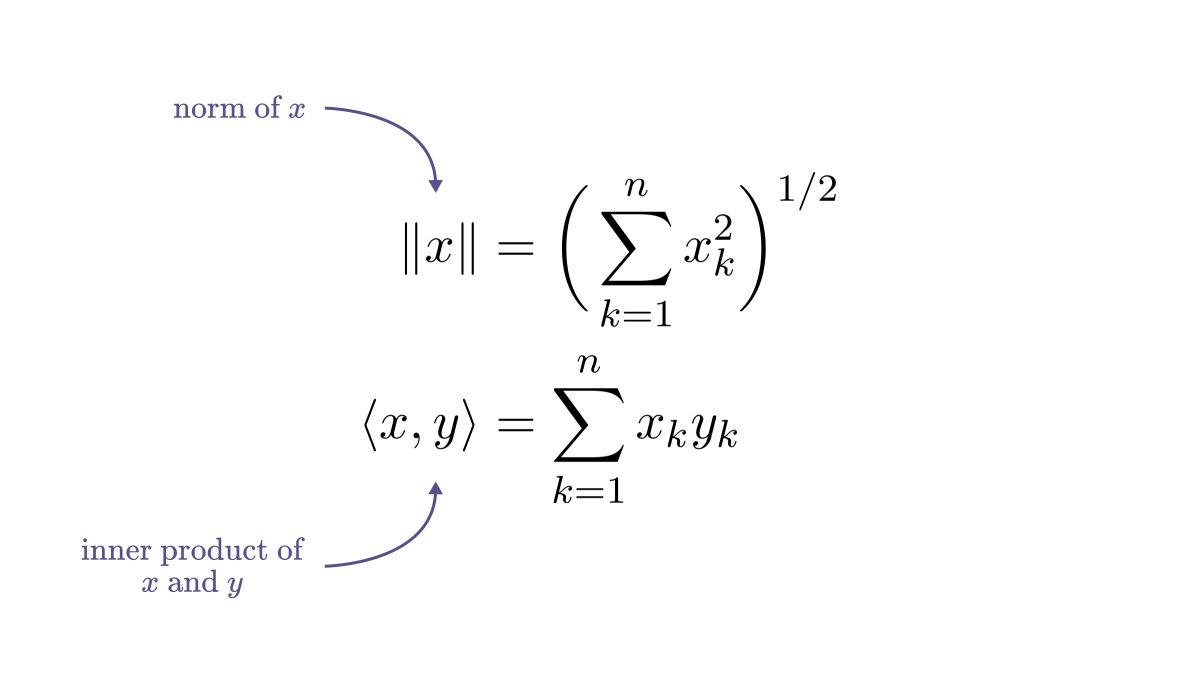
First, let's start with the definition of the logarithm.

The base 𝑎 logarithm of 𝑏 is simply the solution of the equation 𝑎ˣ = 𝑏.

Despite its simplicity, it has many useful properties that we take advantage of all the time.

You can think of the logarithm as the inverse of exponentiation.

Because of this, it turns multiplication into addition. Exponentiation does the opposite: it turns addition into multiplication.

(The base is often assumed to be a fixed constant. Thus, it can be omitted.)

Why is this useful? For calculating gradients and derivatives!

Training a neural network requires finding its gradient. However, lots of commonly used functions are written in terms of products.

As you can see, this complicates things.

By taking the logarithm, we can compute the derivative as it turns products into sums.

This method is called logarithmic differentiation.

Since the logarithm is increasing, maximizing a function is the same as maximizing its logarithm. (Same with minimization.)

One example where this is useful is the maximum likelihood estimation.

Given a set of observations and a predictive model, we can write this in the following form.

Believe it or not, this is behind the mean squared error.

Every time you use this, logarithms are working in the background.

If you enjoyed this thread and want to see behind the curtain of machine learning, I am writing a book for you, where we go from high school math to neural networks, one step at a time.

The early access for Mathematics of Machine Learning is out now!

tivadar.gumroad.com/l/mathematics-…

https://twitter.com/jonathanalis1/status/1445493660737421322

More applications of logarithms: transforming data for visualization. This is extremely useful in life sciences, where the scale of features is exponential.

https://twitter.com/jonathanalis1/status/1445493660737421322

https://twitter.com/kylewadegrove/status/1445472670435274753

And one more: numerical stability. When a computation involves very large numbers, taking the log can help avoid overflow.

https://twitter.com/kylewadegrove/status/1445472670435274753

• • •

Missing some Tweet in this thread? You can try to force a refresh

This Thread may be Removed Anytime!

Twitter may remove this content at anytime! Save it as PDF for later use!

More from @TivadarDanka

Tivadar Danka

@TivadarDanka

4 Oct

As you know, I am working on teaching mathematics in a way that maximizes value for machine learning practitioners.

Do you have any work stories where mathematical knowledge was a genuine advantage?

I would appreciate it if you could share!

I'll start. ↓

As a bioimage analyst, one of my projects involved the pixel-perfect identification of very thin objects: plant seedlings. (Like below.)

This was a classical semantic segmentation problem.

At first, I trained a UNet model using cross-entropy loss, but it didn't quite work.

The problem was that on the segmentation output, objects were not defined at all. My model predicted almost every pixel as background.

With some basic mathematical thinking, I suspected that the problem is caused by the cross-entropy loss.

Read 8 tweets

Tivadar Danka

@TivadarDanka

30 Sep

🤔 Should you learn mathematics for machine learning?

Let's do a thought experiment! Imagine moving to a new country without speaking the language and knowing the way of life. However, you have a smartphone and a reliable internet connection.

How do you start exploring?

1/8

With Google Maps and a credit card, you can do many awesome things there: explore the city, eat in nice restaurants, have a good time.

You can do the groceries every day without speaking a word: just put the stuff in your basket and swipe your card at the cashier.

2/8

After a few months, you'll start to pick up some language as well—simple things, like saying greetings or introducing yourself. You are off to a good start!

There are built-in solutions for common tasks that just work. Food ordering services, public transportation, etc.

3/8

Read 8 tweets

Tivadar Danka

@TivadarDanka

29 Sep

I just released a new chapter for the early access of my book, the Mathematics of Machine Learning!

This week, we are diving deep into the geometry of matrices.

What does this have to do with machine learning? Read on to find out. ↓

tivadar.gumroad.com/l/mathematics-…

Matrices are the basic building blocks of learning algorithms.

Multiplying the data vectors with a matrix is equivalent to transforming the feature space. We think about this as a "black box", but there is a lot to discover.

For one, how they change the volume of objects.

This is described by the determinant of the matrix, which is given by

• how the transformation scales the volume,
• and how it changes the orientation of basis vectors.

The determinant is given by the formula below. I am a mathematician, and even I find this intimidating.

Read 5 tweets

Tivadar Danka

@TivadarDanka

21 Sep

You don't need to go to a university to learn machine learning - you can do it from your living room, for completely free.

Here is an extensive list of curated free courses and tutorials, from beginner to advanced. ↓

(Trust me, you want to bookmark this tweet.)

This is how I'll group the courses.

Machine learning
├── Getting started
├── Computer vision
├── NLP
├── Reinforcement learning
└── Applications

Coding
├── Python
├── R
├── Javascript
└── Machine learning frameworks

Let's start!

@3blue1brown

Machine learning
└── Getting started

1. Neural networks (by @3blue1brown)

youtube.com/playlist?list=…

Read 40 tweets

Tivadar Danka

@TivadarDanka

20 Sep

What do you get when you let a monkey randomly smash the buttons on a typewriter?

Hamlet from Shakespeare, of course. And Romeo and Juliet. And every other finite string that is possible.

Don't believe me? Keep reading. ↓

Let's start at the very beginning!

Suppose that I have a coin that, when tossed, has a 1/2 probability of coming up heads and a 1/2 probability of coming up tails.

If I start tossing the coin and tracking the result, what is the probability of 𝑛𝑒𝑣𝑒𝑟 having heads?

To answer this, first, we calculate the probability of no heads in 𝑛 tosses. (That is, the probability of 𝑛 tails.)

Since tosses are independent of each other, we can just multiply the probabilities for each toss together.

Read 14 tweets

Tivadar Danka

@TivadarDanka

16 Sep

Data similarity has such a simple visual interpretation that it will light all the bulbs in your head.

The mathematical magic tells you that similarity is given by the inner product. Have you thought about why?

This is how elementary geometry explains it all.

↓ A thread. ↓

Let's start in the beginning!

In machine learning, data is represented by vectors. So, instead of observations and features, we talk about tuples of (real) numbers.

Vectors have two special functions defined on them: their norms and inner products. Norms simply describe their magnitude, while inner products describe
.
.
.
well, a 𝐥𝐨𝐭 of things.

Let's start with the fundamentals!

Read 11 tweets

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Too expensive? Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal Become our Patreon

Thank you for your support!

Share this page!

Tivadar Danka

Try unrolling a thread yourself!

More from @TivadarDanka

Tivadar Danka

Tivadar Danka

Tivadar Danka

Tivadar Danka

Tivadar Danka

Tivadar Danka

Did Thread Reader help you today?

Like this author's thread?