Share this page!

Enter URL or ID to Unroll

You can paste full URL like: https://x.com/threadreaderapp/status/1644127596119195649
or just the ID like: 1644127596119195649

How to get URL link on X (Twitter) App

  1. On the Twitter thread, click on or icon on the bottom
  2. Click again on or Share Via icon
  3. Click on Copy Link to Tweet
  4. Paste it above and click "Unroll Thread"!
  5. More info at Twitter Help
Rosana Ferrero 📈📊🙌 Profile picture
@RosanaFerrero
Oct 31, 2022 • 12 tweets • 13 min read • Read on X
Scrolly
🤯Tercer y última parte de ERRORES QUE DAN MIEDO en #DataScience 🎃

☠️ERRORES mortales que incluso los expertos cometen⚰️
rosanaferrero.blogspot.com/2016/09/los-7-…

Continúa leyendo, si te atreves...👻
#HorrorStats #HappyHalloween #DataAnalytics #Halloween #FelizLunes #dataviz #RStats #Python #ML
🚫No realizar una investigación reproducible💀

“Every analysis you do on a dataset will have to be redone 10-15 times before publication. Plan accordingly” Trevor A.Branch

No crear un informe replicable, reproducible y reutilizable sí que DA MIEDO

#HorrorStats #HappyHalloween
🚫No seleccionar la prueba de hipótesis o el modelo de regresión correcto para tu objetivo🎃

¿Cuáles son las hipótesis? ¿Cómo son las muestras? ¿Qué tipo de prueba/modelo elegir? ¿Una cola o dos colas? ¿Qué hacer si mis datos no cumplen los supuestos? BOOO!! 👻

#HorrorStats #ML
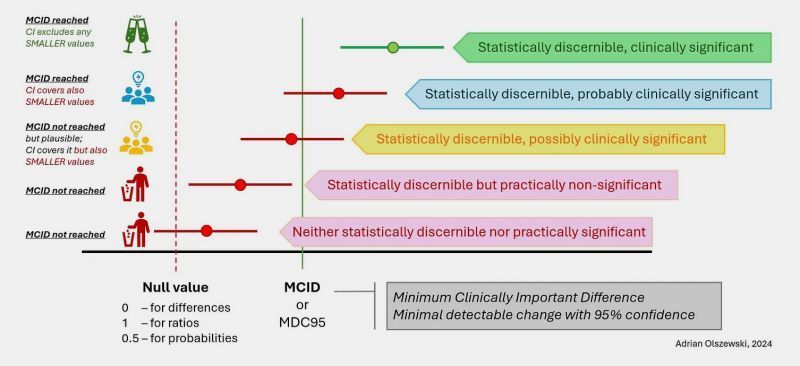
🚫No distinguir la significación estadística de la significación práctica🤦🏻‍♀️p-valor nos dice la dirección y tamaño del efecto la magnitud

Que exista una diferencia no significa que sea grande

Muestras muy grandes detectan diferencias muy pequeñas. Big Data da MIEDO!
#HorrorStats
🚫Decir "se comprueba la hipótesis nula H0" o "H0 es cierta"

👉Así como la falta de evidencia no demuestra que el acusado es inocente, un resultado no estadísticamente significativo (e.g. p>.05) no demuestra que H0 sea verdadera. Solo “no hay suficiente evidencia"💀
#HorrorStats
🚫Decir "el p-valor es la probabilidad de que H0 sea cierta"

😱Las hipótesis son o no son. p-valor mide la fuerza de la evidencia contra H0. A menor p-valor, mayor evidencia contra H0 a largo plazo🧙

Sientes ESCALOFRÍOS?
#HorrorStats #DataScience #Halloween2022 #RStats #Python
🚫Considerar que el nivel de significación alfa=5% es un mandamiento⛪️

😉El valor 5% es simplemente una convención conveniente, podría ser el 10% o el 1%, no existe un umbral real.

🎃#HorrorStats #DataScience #RStats #Python #Analytics #dataviz #analisisdedatos 👻
Lee más👇
🚫No informar el p-valor exacto ni los resultados completos de la prueba de hipótesis.

😱p-valor depende de:
📌tamaño de efecto (ES), ES grandes son más fáciles de detectar.
📌tamaño de muestra (N). muestras grandes dan pruebas más sensibles
📌Diseño de estudio...

#HorrorStats
🚫No considerar el Error tipo III: resolver el problema incorrecto.

☠️¿Las hipótesis son las correctas? ¿Cuán plausible es H0? ¿Cuáles son las consecuencias de rechazar H0? El contexto es crucial

👻#HorrorStats #Halloween #Halloween2022 #DataScience #dataviz #RStats #Python 🎃
🚫Desconocer la potencia estadística

¿Alguna vez te lo has preguntado?
👉¿Puedo confiar en el resultado?
👉¿Cuántas muestras necesito?

Conocer la potencia estadística nos permite ahorrar tiempo y dinero en nuestras investigaciones, ¡¿cómo no te lo contaron antes?!

#HorrorStats
Interpretar correctamente los resultados de un análisis puede ser muy difícil😱

😎Para volverte un PRO en #DataScience no cometas los errores que te he mostrado en este hilo y usa esta guía para planificar y diseñar investigaciones rigurosas👇
#Halloween
maximaformacion.es/recursos/disen…
Recuerda👇

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Rosana Ferrero 📈📊🙌

Rosana Ferrero 📈📊🙌 Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @RosanaFerrero

Rosana Ferrero 📈📊🙌 Profile picture
Mar 30
🚨 Una crítica válida y urgente a prácticas comunes de análisis de datos en la Ciencia🚨

🏆 La causalidad es el Santo Grial del análisis de datos: saber qué realmente causa qué. Pero, ¡cuidado! No es tan fácil como parece. Image
🧠 La causalidad (especialmente en medicina y salud pública) NO es como un interruptor de luz. 🔦 Prendes, se enciende. Apagas, se apaga. Fácil. La causalidad aquí es clara debido a mecanismos conocidos, resultados inmediatos y repetibles. Image
😱 Pero en otros ámbitos (como en la salud)… la cosa se complica. Factores como intervenciones poco definidas, sistemas complejos (biológicos/sociales) y mediciones imprecisas dificultan establecer la causalidad. 🤔

💣 Hay 3 tipos de investigadores que fracasan con esto: 👀 Image
Read 7 tweets
Rosana Ferrero 📈📊🙌 Profile picture
Mar 2
🤯 Por piensas que con solo mirar coeficientes y R² tienes todo bajo control en tu modelo de regresión... 🤨

🔥 El Cuarteto de Anscombe: Cuatro datasets, un mismo modelo… pero con realidades completamente distintas. 🔥

🧵Soluciones...👇

#stats #analytics #datascience #DataViz Image
Estos cuatro conjuntos de datos tienen:
✅ Misma media en X e Y
✅ Misma varianza
✅ Misma correlación
✅ Mismos coeficientes de regresión
✅ Mismo R²

📉 Pero cuando los graficas… descubres el desastre 🤯

💡 Errores clave en un modelo de regresión:
❌ 1. Asumir linealidad sin verificarla
No todas las relaciones son lineales. Ajustar una línea recta a un patrón curvo es un error clásico.
Solución: Graficar y evaluar modelos más flexibles como regresión con splines o GAM.
Read 7 tweets
Rosana Ferrero 📈📊🙌 Profile picture
Feb 26
🔥 ¿QUÉ MODELO DE REGRESIÓN DEBERÍAS ELEGIR? (UNA GUÍA SENCILLA) 🔥

¿No sabes qué modelo de regresión usar? ¿Te confunden los términos LM, GLM, GAMM y demás siglas raras? 🌀 LO INTENTARÉ EXPLICAR RÁPIDAMENTE ⏳💥👇🧵

#stats #analytics #datascience Image
📢 PASO 1: ¿Tu variable respuesta es continua?
✅ Sí → Modelo Lineal (LM) (SI SE CUMPLEN SUS SUPUESTOS).
🚫 No → ¡Sigue leyendo! 👇
📢 PASO 2: ¿Tu variable respuesta es binaria, de conteo o de proporciones?
✅ Sí → Modelo Lineal Generalizado (GLM) (elige la familia adecuada: binomial, Poisson, gamma, etc.)
🚫 No → Vamos más profundo. 👇
Read 8 tweets
Rosana Ferrero 📈📊🙌 Profile picture
Feb 25
🚨📊 ¿Por qué deberías dejar de usar barplots? 🌧️🌈

Si sigues usando gráficos de barras con error para representar datos cuantitativos, estás perdiendo información valiosa. Aquí te explico por qué:👇🧵

#DataViz #RaincloudPlots #Analytics #RStats #DataScience #stats Image
1️⃣🔥 Ocultan la variabilidad → ¡Pueden hacer que datos diferentes se vean iguales!😵
👉📊 Los barplots NO te muestran la forma real de los datos, solo la media y el error o la incertidumbre.
🚨Datos con distribuciones totalmente diferentes pueden parecer idénticos en un barplot. Image
2️⃣ 🤯 Malas comparaciones → ¡Pueden hacerte creer diferencias que no existen! 📉
👉📊 Si los tamaños de muestra son diferentes, los IC en los barplots pueden ser engañosos.
❌ Dos grupos =medias y !=N pueden generar IC que te hagan pensar que hay +o- incertidumbre de la real. Image
Read 9 tweets
Rosana Ferrero 📈📊🙌 Profile picture
Feb 22
🔥 Crear gráficos con pruebas estadísticas suele requerir varios pasos, pero {ggstatsplot} lo hace todo en una sola línea de código. 👇🧵

✅ No necesitas copiar/pegar números en un informe: los gráficos ya contienen toda la información.

#rstats #stats #dataviz #datascience Image
🎯 #stats + #dataviz en 1 solo paso
✅ Gráficos con pruebas paramétricas, no paramétricas y robustas
✅ Formato APA listo para publicar 📑
✅ Muestra automáticamente N 📊
✅ Mezcla caja + violín para mejor visualización 🎻
✅ Incluye tamaños de efecto, IC y pruebas bayesianas Image
Image
Image
Image
📌 Funciones:
📊 ggbetweenstats → Compara entre grupos (violín + caja)
📊 ggwithinstats → Compara dentro de grupos
📊 gghistostats → Histogramas
📊 ggscatterstats y ggcorrmat → Correlaciones
📊 ggbarstats y ggpiestats → Barras y pie
📊 ggcoefstats → Regresión y metaanálisis Image
Read 5 tweets
Rosana Ferrero 📈📊🙌 Profile picture
Feb 18
🧐 Si quieres gráficos rápidos, elegantes y sin sufrir, prueba {tinyplot}🔥
✅ Gráficos en base R sin complicaciones
✅ Agrupaciones y leyendas automáticas en un solo paso
✅ Facetas sin sudar la gota gorda (olvídate de par(mfrow=...))
✅ Temas personalizables con un solo comando Image
📌 ¿Por qué deberías probar tinyplot?
1️⃣ Usa solo base R → sin dependencias, sin bloat.
2️⃣ Ultra ligero → instalación mínima, ideal para paquetes o scripts portables.
3️⃣ Drop-in replacement → si ya usas plot(), cambiar a tinyplot() es pan comido. Image
Image
🎯 ¡Prueba esto AHORA MISMO en tu R! 🎯
install.packages("tinyplot")
library(tinyplot)

plt(Sepal.Length ~ Petal.Length | Species, data = iris,
palette = "dark", pch = 16, grid = TRUE, frame = FALSE)

🌈 Y obtén un scatterplot agrupado con leyenda automática en una línea. Image
Read 4 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Don't want to be a Premium member but still want to support us?

Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Follow Us!

Send Email!

:(