Thread by @ClaraGrima

Como está la cosa muy fea vamos a compartir algo bonito, sobre todo, algo elegante.

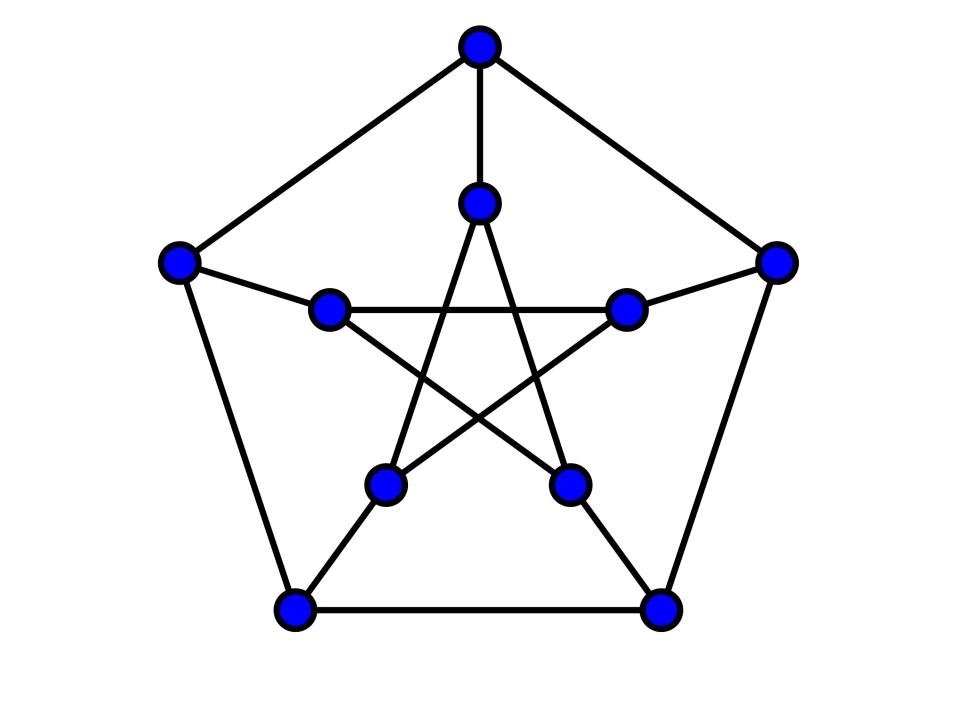
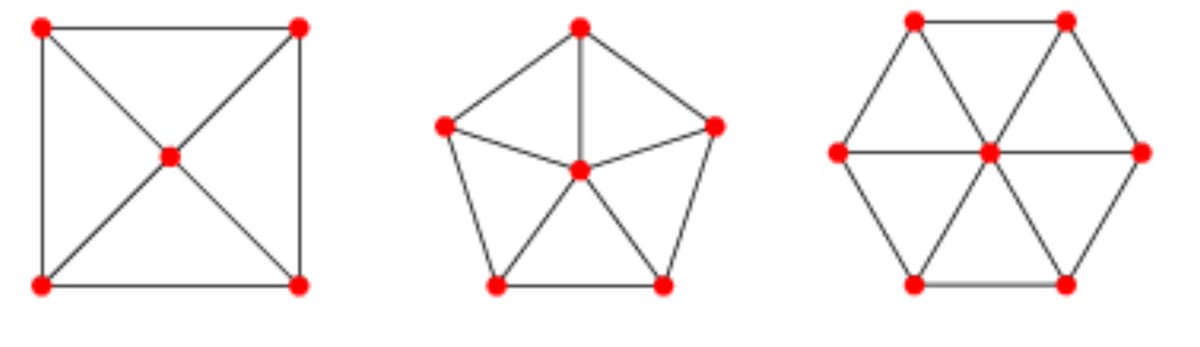
Me refiero a algo sobre grafos, cómo no.

Sigue este hilo que te va a encantar :)

#WeWillMathYou #WeAreAllGraphsHere

Un grafo, como ya sabéis los que me seguís, es un objeto matemático formado por dos conjuntos. Un primer conjunto de vértices o nodos (que representamos con puntitos) y un segundo conjunto de aristas (que unen a algunos de estos puntitos por parejas).

Podéis pensar en Facebook, por ejemplo. Los usuarios serían vértices y unimos con aristas aquellos vértices que sean amigos en dicha red social.

Podemos hacer cosas muy preciosas con los grafos pero hoy os quiero contar algo que tiene que ver con el etiquetado de los mismos. Si etiquetamos usando un número entero no negativo ({0, 1, 2, ...}) cada uno de los vértices dicho etiquetado inducirá un etiquetado de las aristas.

Por ejemplo, podemos etiquetar cada arista con el resultado de restar el valor de las etiquetas de los vértices que une dicha arista, el mayor menos el menor para que siempre tengamos números enteros no negativos.

Esta mañana queremos todo positivo (o cero), nada negativo ;-)

Pues bien, se dice que un grafo con N aristas es ELEGANTE (graceful) si podemos poner etiquetar a sus vértices usando números enteros no negativos ({0, 1, 2, 3, ... }) de tal forma que sus aristas queden etiquetadas desde 1 hasta N.

Veamos un ejemplo :)

El grafo del tuit anterior tiene 12 aristas. Tenemos que etiquetar sus vértices usando números enteros no negativos para que sus aristas queden etiquetadas desde 1 hasta 12.

¿Se podrá? ¿Te atreves a intentarlo antes del siguiente tuit que muestra una posible solución? ;-)

Yo creo que este etiquetado de los vértices es bastante elegante, ¿no crees? ;-)

Siento decirte que la elegancia en grafos no depende de tu opinión, está bien definida para todos los seres pensantes de este planeta. Bueno, y para cualquier ser inteligente de este universo. Y de los paralelos ;-)

Vamos a comprobar su elegancia con este gif :)

Según decía mi 'amigo' Paul Erdős, la mayoría de los grafos no son elegantes :(

Pero el grafo de Petersen (que tiene 15 aristas) sí lo es :)

¿Te atreves a demostrar que es elegante etiquetando los vértices para que las aristas queden etiquetadas desde el 1 al 15

Estos grafos también son elegantes.

¿Te atreves a demostrarlo? ;-)

Yo creo que es un bonito pasatiempo para la clase de mates en primaria y secundaria :)

Esta es una de las razones por las que AMO las matemáticas: ni la elegancia depende de nuestra opinión :)

No como en la vida real en la que el concepto de elegancia tiene razones que mi razón no entiende.

Y ya.

Que tengas un día bonito y no te dejes engañar por los hombres grises :)

Actualización: @lolamenting me ha preguntado por un ejemplo de grafo no elegante y he grabado un vídeo cutre para explicar por qué K5 no es elegante :)

@lolamenting @threadreaderapp unroll