Thread by @Cuent_Cuanticos

La entropía, el desorden, la segunda ley de la termo, Boltzmann, Planck y la cuántica

Usualmente se suele definir la entropía como:

La entropía es la medida del desorden de un sistema.

Y esta es, posiblemente, una de las peores definiciones de una magnitud física que se precie.

En pocas palabras, la entropía es esto:

¿Qué os parece?

Vale, vale...

S es la entropía
ln es logaritmo neperiano
W es el número de configuraciones de los constituyentes de un sistema que son compatibles con el estado que observamos en dicho sistema.

¿Mejor ahora?

Vamos a ver qué significa todo eso. Para ello vamos a tomar un ejemplo muy simple.

1) Tenemos un contenedor de un determinado volumen en el que identificamos su mitad derecha y su mitad izquierda.

2) Tenemos 4 partículas idénticas.

Ahora vamos a calcular configuraciones en ese sistema. Vamos a calcular las posibles W.

¿Va?

Supongamos que estamos en una situación en la que las cuatro partículas están en el lado izquierdo. ¿Cuántas configuraciones posibles hay?

Hay una única configuración. Porque en principio tenemos que repartir 4 partículas pero una vez que están en el lado izquierdo nos da exactamente igual el orden en el que se encuentren. Por lo tanto, hay 4! ordenaciones de 4! pero todas son equivalentes para nuestros propósitos

¿Qué pasa si hay 3 partículas a la izquierda y 1 a la derecha? Bueno, pues tendremos las configuraciones:

En este caso las ordenaciones de cada situación entre las tres de la izquierda nos dan exactamente igual, por eso se divide por 3!.

Si tenemos 2 y 2, a derecha e izquierda, ya tendrás claro que lo que vamos a obtener es:

Evidentemente ahora podríamos seguir pasando más partículas a la derecha. No lo haremos porque obtendríamos los mismos resultados... La simetría es lo que tiene.

Si nuestras partículas tienen la misma probabilidad (1/2) de estar a izquierda o derecha, las distintas configuraciones serán más o menos probables cuanto mayor sea su número.

En el primer caso tenemos 1 configuración por (1/2)(1/2)(1/2)(1/2)

En el segundo caso tenemos 4x(1/16)

En el tercer caso tenemos 6x(1/16).

Eso implica que si dejamos al sistema evolucionar será más probable encontrar la situación de tener las partículas repartidas por todo el volumen que tenerlas en tal o cual mitad.

Es decir, que el sistema evoluciona hacia el estado que presenta mayor número de configuraciones.

Eso es la segunda ley de la termo que nos dice que la entropía en un sistema aislado aumenta o permanece constante.

Así se explica que no es probable que todas las moléculas de aire de tu habitación se vayan a la vez a una esquina y mueras de asfixia.

Por lo tanto, podemos decir que la entropía es el número de configuraciones:

S=W.

Valeeeee... ¿Qué pasa con el logaritmo?

El tema está que en termodinámica sabemos que si mezclamos dos sistemas la entropía del conjunto es la suma de entropías (al menos).

Pero si un sistema tiene W1 configuraciones posibles y el otro W2 las configuraciones totales de la mezcla serán:

W=(W1)(W2).

Es decir, si la entropía fuese directamente W no sería aditiva sino multiplicativa.

No pasa nada, si decimos que S=ln W la cosa se soluciona.

¿Por qué? Pues porque...

ln(AB)=ln(A)+ln(B)

Entonces, considerando que los sistemas están compuestos por constituyentes elementales (partículas, átomos, moléculas, etc) y que podemos hacer estas piruetas combinatorias damos con una explicación de qué es la entropía y de la segunda ley de la termodinámica.

Eso sí... Cuando tenemos sistemas en estados que tienen pocas configuraciones posibles decimos que están ordenados. Si hay muchas configuraciones posibles decimos que están desordenados.

Como los sistemas (aislados) aumentan la entropía van siempre a estados con muchas configuraciones posibles. Van hacia donde el "desorden" es máximo.

¿Y qué tiene que ver todo esto con Boltzmann, Planck y la cuántica?

El ejemplo que hemos puesto de las partículas en el recipiente no es mentira pero no se suele pensar así.

Usualmente pensamos en términos energéticos y nos preguntamos cuántas partículas tienen tal o cual energía elemental si el sistema grandote tiene una energía E.

Así, nuestras cajas anteriores ahora representan niveles de energía. Supongamos que nuestras partículas pueden tener una energía E1 o una energía E2.

El problema es exactamente igual que el anterior solo que ahora en vez de repartir las partículas en lados de un contenedor lo hacemos en distintos niveles de energía.

Pero un momento...

Digamos que las energía son:

E1= 15.5

E2=31.0

Lo que estamos asumiendo es que las partículas solo pueden tener esas energías y ninguna otra. No puede haber una energía de 16.34 por ejemplo.

Nota para tiquismiquis:

En el tuit anterior estamos trabajando con unidades naturales de la energía.

Para calcular la entropía hemos de asumir que las energías posibles de las partículas están discretizadas.

Si no se hace así... la entropía no puede ser definida.

(Ojo, nadie aquí está diciendo que no se pueda tomar el límite al continuo pero la discretización que subyace deja huella)

Pues bien, el primero en introducir argumentos probabilísticos para definir la entropía fue Boltzmann.

Joder, si pusieron la fórmula en su tumba:

Eso sí, Boltzmann jamás escribió esa fórmula en los artículos de 1872 y 1877 que abrieron este campo de la física.

Pero vamos, que no le hacía falta escribirla, de esos escritos se deduce esa bonita fórmula y por eso todo el mundo se la asigna.

Aquí tenéis el artículo de 1877:

semanticscholar.org/paper/Translat…

Donde se puede leer:

Se me ponen los pelos de gallina...

Por supuesto, estos resultados tuvieron poco éxito entre colegas de profesión. Hay dos razones fundamentales para ello:

a) Nadie creía que una magnitud física fundamental como la entropía tuviera una definición probabilística.

b) Casi nadie creía en los átomos.

Y dando un salto en la historia llegamos a diciembre de 1900. Un tal Planck inicia la era cuántica de la física al dar una explicación del equilibrio entre la radiación y la materia estudiando eso que se llama cuerpo negro.

Para explicar eso Planck tiene que introducir una constante universal nueva, la constante de Planck h, y tiene que asumir que la energía está discretizada...

Se cuenta por ahí que Planck consideró eso como un acto de desesperación para poder explicar el comportamiento de un sistema radiación/materia en equilibrio.

¿Cuál fue el acto de desesperación? ¿Aceptar que la energía estaba discretizada?

La verdad es que Planck tuvo que asumir las ideas de Boltzmann. Planck se había pasado la vida estudiando la entropía y creía que tenía una definición absoluta y no probabilística.

Le repugnaba el trabajo de Boltzmann sobre la entropía.

Y sin embargo, en 1900, después de mucho, mucho tiempo pensando en el problema tuvo que...

(hermes.ffn.ub.es/luisnavarro/nu…)

Así, el bueno de Planck tuvo que usar la entropía del sistema radiación/materia a la Boltzmann y por consiguiente tuvo que introducir una discretización de la energía.

Evidentemente llegó a calcular la constante que rige el comportamiento cuántico, cosa que Boltzmann no hizo, y posteriormente se confirmo que la energía de los sistemas confinados y de los fotones está discretizada. Así se inició la cuántica.

Lo que es innegable es que las ideas de Boltzmann ya anticipaban todo eso. Y Planck pudo explicar el problema del equilibrio radiación/materia porque se propuso calcular la entropía. Y claro, la entropía ya sabía cuántica antes que Planck y que los demás.

Por cierto, el primero en escribir la fórmula de la tumba de Boltzmann fue un tal Planck en 1901:

strangepaths.com/files/planck19…

Un par de cosas finales.

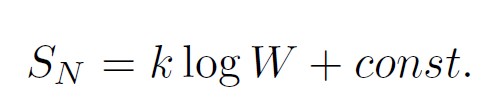
Planck hablando de todo esto y de Boltzmann:

Y esta preciosa charla de @lauramorron sobre Boltzmann en @Naukas_com.

eitb.tv/es/video/nauka…