Thread by @PhDJokesMemes

Machine Learning - IX
- Seshadhiri Dhanasekaran

இன்று நாம் காண இருக்கும் டாபிக் Gradient Descent. இது ஒரு optimization (மேம்படுத்தல்) முறை.

#MachineLearningTamil
#Thread
#MachineLearning

ML algorithmகள் டேட்டாவில் எப்படி உருவானது என கற்கும்போது அதன் கற்றல் திறனை (learning rate and fitting) மேம்படுத்த உதவும். இதில் Gradient Descent தான் அதிகமாக பயன்படுத்த படுகிறது. இந்த gradient descentல பல வகைகள் உள்ளன.

1. Stochastic Gradient Descent
2. Batch Gradient Descent
3. Mini Batch Gradient Descent

Gradient Descent என்ன என்பதை புரிந்து கொள்ள ஒரு ஈசி உதாரணம். நீங்கள் மலையில் சிக்கி இருந்து இறங்க முயற்சி பண்றீங்க. என்ன பிரச்சனைன்னா சுத்தி ஒரே பனி மூட்டமாக இருக்கு. மலையின் கீழே உள்ள பாதை தெரியவில்லை.

எனவே குறைந்தபட்ச பாதையை கண்டுபிடிக்க உள்ளூர் தகவல்களை கொண்டு சுத்தி பக்கத்துல தெரியுற safe ஆன பகுதியா நகர்ந்து செல்ல வேண்டும்.

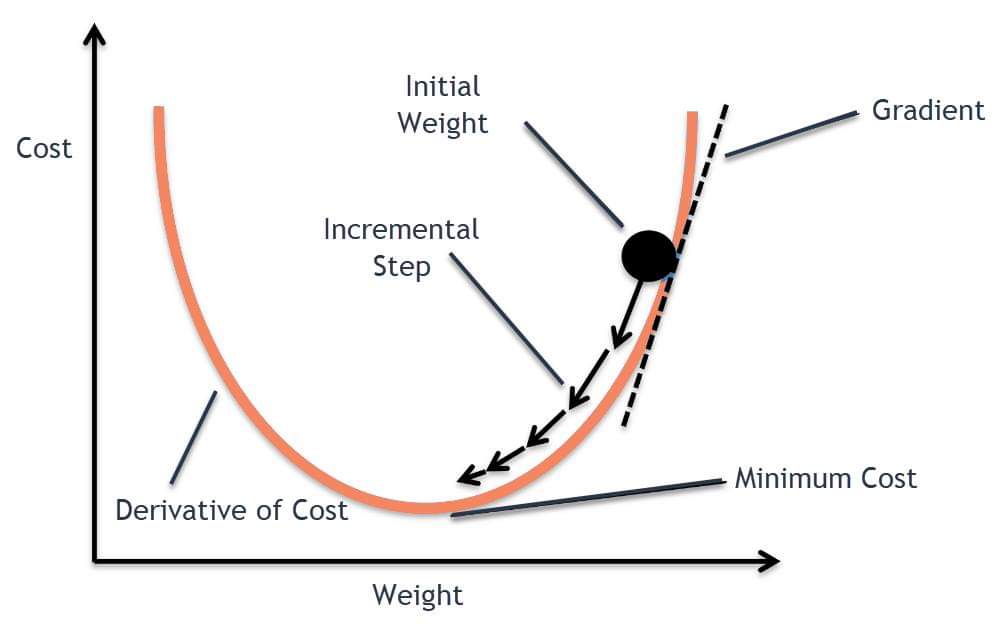
நீங்க இருக்க பொஸிஷன்ல இருந்து மலை உச்சியை பார்த்து கண்னுக்கு தெரிந்த பக்கத்தில் உள்ள பகுதிகளை கொண்டு அப்படியே கீழ இறங்க வேண்டும்.

கீழ இவ்ளோ தூரத்தில் மலையடிவாரம் இருக்கலாம் என்று மெதுவாக கடந்து செல்லலாம்.
பக்கத்துல இருக்க safe ஆன பகுதிகளை கடந்து கடந்து , மினிமம் பாயிண்ட் அடைவதே இது . இதற்க்கு கீழ உள்ள படம் உங்களுக்கு உதவும்.

இதை நீங்க 0வில் இருந்து ஆரம்பிக்க வேண்டும். coefficient = 0:0

பின்பு ஒரு தடவை Iteration (கற்றல் ) நடந்த பின் அதற்க்கான cost கண்டுபுடிக்க வேண்டும். இந்த cost எப்படி கண்டுபிடிப்பது என்றால்

cost = f(coefficient)

cost = evaluate(f(coefficient))

இப்போ அடுத்து இந்த costல derivative (differential calculus) அப்ளை பண்ணனும்
Delta = Derivative(Cost)
கற்றல் ஆரம்பித்த பின் இந்த coefficient value மாறும்
மாறின coefficient value கண்டு புடிக்கணும்
ஆல்பா என்பது learning ரேட் (கற்றல் ஆற்றல்) இது 1 மற்றும் 0க்கு இடையில் தான் இருக்கும்

1 - highest learning rate. 0 - lowest learning rate. இதுக்குள்ள ஒரு நம்பரை நீங்கள் சூஸ் பண்ணனும். அதிகமாவும் போக கூடாது. குறைவாகவும் இருக்க கூடாது.

coefficient = coefficient * (alpha * delta)

இதை திரும்ப திரும்ப செய்யனும். ஒன்னு coefficient 0 ஆகணும் இல்லனா எவ்ளோ பண்ணியும் coefficient ரேட் குறையாத போது நிறுத்த வேண்டும்.

இதை கொண்டு நாளை ஒரு algorithm performance எப்படி மாற்ற முடியும் என்று பார்ப்போம்.

f(x) = x4 – 3x3 + 2, f1 (x) = 4x3 – 9x2 .

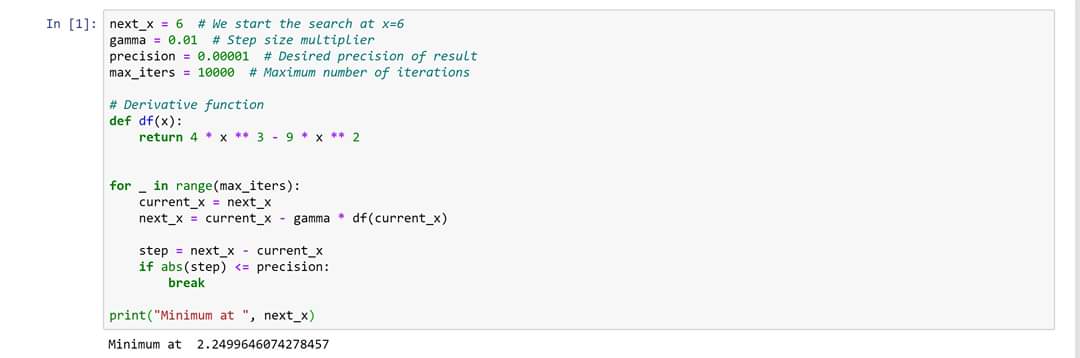
இதை நீங்கள் சால்வ் செய்தால் x = 9/4.

இதில் plateau point 0 , அதிகம் 9/4.

இதை எப்படி pythonல செய்வது என்பதை இணைத்து உள்ளேன்.
#EndofPartIX