Thread by @josenalencar

Imagine que você apostará as suas economias em uma moeda que será jogada para cima. Você sabe que sua chance é 50%.

Você apostaria se alguém te dissesse, antes do jogo, que a moeda está enviesada para um dos lados?

Troque “economias” por “remédios na pandemia”. E segue o fio.

A inclusão da condição “a moeda está enviesada e eu não sei para qual lado” mudou completamente minha chance no jogo da moeda.

A inclusão da simples pergunta “o artigo científico com qualquer medicamento bizarro para COVID-19 tem vieses?” também muda completamente o jogo.

A análise bayesiana dos artigos científicos é bem ilustrada por John Ioannidis em um dos seus papers mais famosos, em que ele afirma “ser possível provar matematicamente que a maioria das pesquisas são falsas”.

A primeira crítica é a quem interpreta artigos baseado apenas em p.

Quantas vezes, nessa pandemia, fomos surpreendidos por notícias do tipo “estudo prova o benefício da hidroxicloroquina”, para no dia seguinte aparecer outro falando “estudo prova que HCQ não tem efeito”? E Annita?

Quantas vezes vimos que ovo faz mal? No dia seguinte faz bem.

Duas pessoas sofrem com isso:

- O leigo, levado pelas manchetes chamativas dos jornais, por paixão política, ou por medo de uma doença falsamente noticiada como “sem tratamento”.
- O médico que acredita em correntes de WhatsApp, como a demonstrada.

Vários tipos lucram com isso:

- O político que apostou nesse medicamento desde o começo, tentando se apoderar do seu suposto benefício;
- O pesquisador que agora terá muitas visualizações e citações, aumentando seu prestígio e sua conta bancária;
- O médico que ilude pacientes.

Como Ioannidis propõe a análise de artigos, então?

- Apresentando o valor R, que é a probabilidade pré-teste da pesquisa. Uma ferramenta mais subjetiva que formal.
Para uma pesquisa ser verdadeira, (1-β) x R precisa ser > 0,05 (ⲁ)

β = poder da pesquisa.
R: probabilidade pré-teste
1 - β = chance de falsos negativos
ⲁ = chance de falsos positivos nos dados pesquisados (não no universo)

Em outras palavras, leve em consideração a PLAUSIBILIDADE de daquilo na sua interpretação.

Tenhamos, por exemplo, o estudo NEGATIVO com Annita que está sendo noticiado como positivo por causa de uma sub-análise substituta que não respeita a correção de Bonferroni (tudo isso quer dizer “ludibriação”):

(1-0,8) x 0,05 = 0,01. Portanto maior que 0,05. Resultado falso.

Olhe que ainda fui benevolente em dar como 5% a probabilidade pré-teste da Annita (R) na fórmula anterior. Vermífugo… vírus… pressão política…

Mas Ioannidis não para aí. Há mais dois problemas a acrescentar: os vieses, e os múltiplos testes por equipes diferentes.

Para adicionar os vieses à fórmula, Ioannidis usa a letra µ, que significará a proporção de achados falsos, mas que acabam sendo apresentados como verdadeiros. O viés em pesquisa pode ser fruto de impossibilidades logísticas e organizacionais ou manipulação proposital.

Para adicionar os múltiplos testes independentes sobre um tema à fórmula, Ioannidis usa a letra n.

Quanto maiores µ e n, menor o valor preditivo positivo do teste.

Observe esse gráfico do próprio artigo que compara a probabilidade pós-teste de acordo com power (80% em A e um underpowered 50% em B), valor de R (abscissa) e µ (linhas coloridas).

Observe que algo com 20% de plausibilidade (lembre que o valor de R é subjetivo), em um estudo com um bom power (80%), mas mais vieses do que usual (µ = 0,2), a probabilidade pós-teste de aquele resultado ser verdadeiro (MESMO COM P SIGNIFICATIVO e bom power) é de apenas 60%.

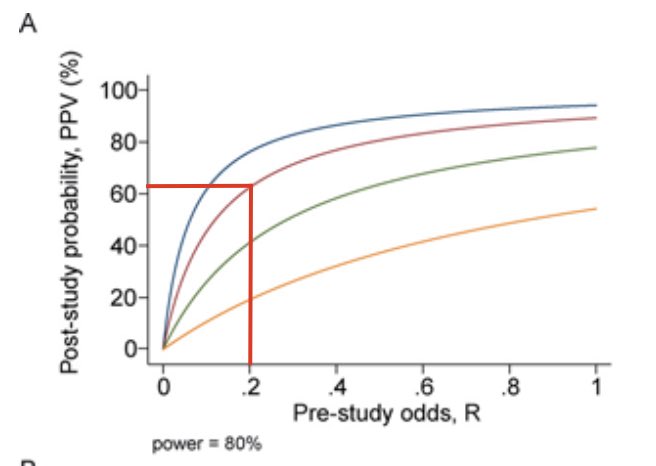
As cores do gráfico também podem refletir a quantidade de estudos realizadas sobre aquele tema. Segundo Ioannidis, quanto mais estudos, mais os vieses e problemas se somam.

É por isso que ovo está todo dia no jornal. Ou cloroquina.

Ioannidis nos brinda com esta ótima tabela auto-explicativa (mas em inglês) que resume seu raciocínio e estima o PPV (valor preditivo positivo) da pesquisa (chance de seu resultado ser verdadeiro). Leia o gráfico como porcentagens (0.85 = 85%).

A tabela é uma maneira de deixar muito claro a qualquer leitor de artigo científico que, em sua interpretação, você precisa levar em conta:
- Plausibilidade da pesquisa (R)
- Quantidade de vieses (µ)
- Power (β)
- Por último o ⲁ.

Ficam ainda seis corolários que transcrevo aqui:
1. Quanto menor o estudo, menor a chance do seu achado ser verdadeiro.
2. Quanto menor o efeito encontrado, menor a chance de ser verdadeiro.
3. Quanto maior o número de relações testadas, menor a chance de ser verdadeiro.

4. Quanto maior a flexibilidade no design, definições e desfechos, menor a chance de ser verdadeiro.
5. Quanto maior o interesse financeiro (e político) em uma pesquisa, menor a chance de ser verdadeiro.
6. Quanto mais “quente” for um tema, menor a chance de ser verdadeiro.

Como melhorar esse cenário?
- Entendendo que é impossível saber com 100% de certeza a verdade absoluta em qualquer pesquisa.
- Pesquisas grandes e metanálises honestas sem vieses podem chegar próximo da “verdade”.
- Não perder tempo com ideias pouco plausíveis (vermífugos, p. ex)

Agora eu convido os colegas médicos a reverem os trials clássicos da sua área de atuação sob essa ótica proposta por Ioannidis.

Você vai se assustar. Bem vindo ao mundo real.

Edit graças às intervenções do colega @ThomasPatrickPB (infelizmente o twitter não permite edição no próprio post):

No nono tweet, onde se lê a fórmula, deve ser:

(1 - 0,2) x 0,05 = 0,04. Portanto MENOR que 0,05, conferindo um resultado falso à pesquisa.

Ainda, no oitavo tweet, β é a chance de falsos-negativos. e 1 - β é o Power.