Thread by @andrewgwils

This is a real problem with the way machine learning is often taught: ML seems like a disjoint laundry list of methods and topics to memorize. But in actuality the material is deeply unified... 1/8

https://twitter.com/dabeaz/status/1398625259708993538

From a probabilistic perspective, whether we are doing supervised, semi-supervised, or unsupervised learning, forming our training objective involves starting with an observation model, turning it into a likelihood, introducing a prior, and then taking our log posterior. 2/8

Our negative log posterior factorizes as -log p(w|D) = -log p(D|w) - log p(w) + c, where 'w' are parameters we want to estimate, and 'D' is the data. For regression with Gaussian noise, our negative log likelihood is squared error. Laplace noise? We get absolute error. 3/8

Softmax observation model? We get the standard cross-entropy classification loss. We can create more tailored loss functions by considering other observation models. Maybe we want to use a probit link function for our observation model instead of logistic sigmoid. 4/8

Choose a Gaussian prior p(w) and you get L2 regularization. What about L1? Just choose a Laplace prior. We can create more tailored regularizers by considering other prior distributions that make sense for our problem at hand. 5/8

Indeed the mechanics of regression, classification, density estimation, generative modelling, clustering, and dimensionality regression are essentially identical. They are all just closely related examples of the same general formulation. 6/8

Want k-means clustering? It's just a special case of EM for Gaussian mixture density estimation. Want PCA dimensionality reduction? It's just maximum likelihood density estimation with a simple factor observation model and Gaussian noise, x = Pz + e. The list goes on! 7/8

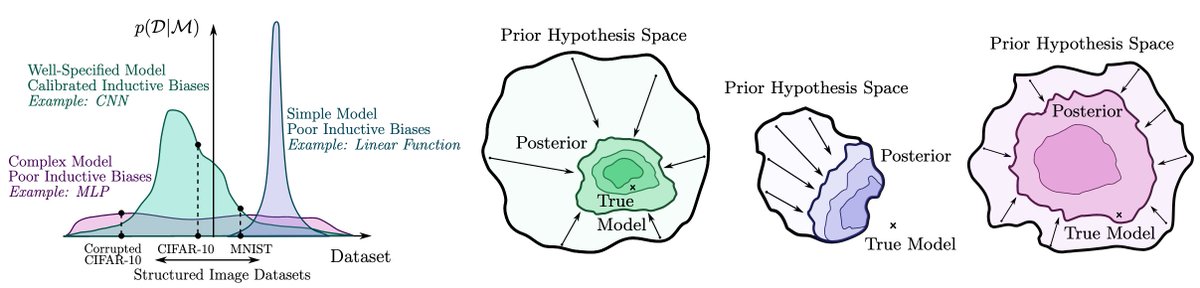
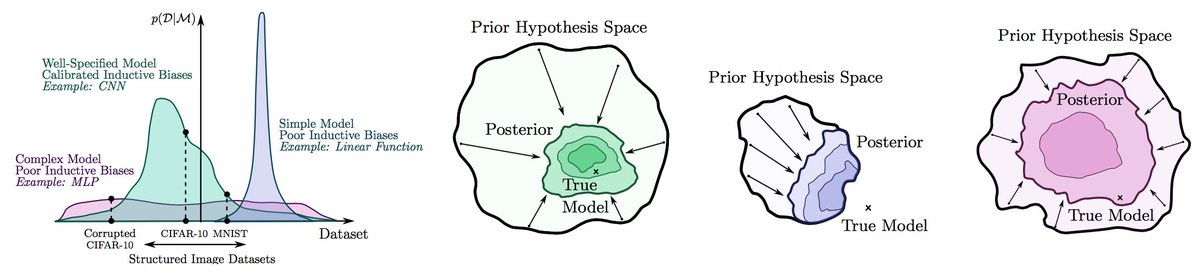
Model construction similarly follows the same principles in any of these settings. We want a flexible model that can express any solution we think is possible. But we also need inductive biases so that reasonable solutions are a priori likely. E.g., arxiv.org/abs/2002.08791 8/8