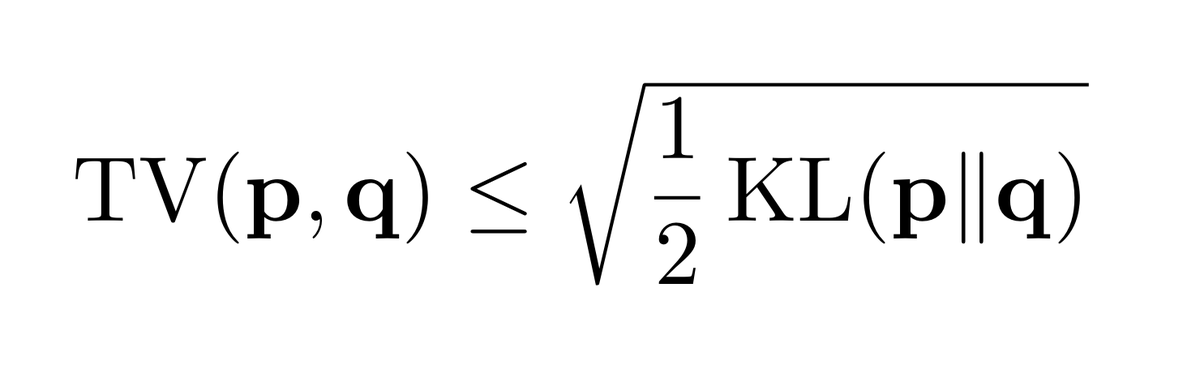Ninth #AcademicSpotlight: Donlapark Ponnoprat (@BomNaKub), Lecturer at @cmuofficial_tw
Paper: Universal Consistency of Wasserstein k-NN classifiers 📝
arxiv.org/abs/2009.04651
Pitch: understanding universal consistency of the k-NN classifier under Wasserstein distances!
1/4
Paper: Universal Consistency of Wasserstein k-NN classifiers 📝
arxiv.org/abs/2009.04651
Pitch: understanding universal consistency of the k-NN classifier under Wasserstein distances!
1/4
In more detail: A binary classifier g(Dₙ) trained on dataset Dₙ is universally consistent (UC) if the error proba Pₓ,ᵧ(g(Dₙ)(X)≠Y|Dₙ) converges to the Bayes risk as n→∞, regardless of the joint distribution of X and Y. This paper studies the universal consistency...
2/4
2/4
... of the k-NN classifier on spaces of proba measures under p-Wasserstein distance. From studying geometric properties of Wasserstein spaces, we show that the k-NN classifier is (1) UC for any p≥1 on the space of measures finitely supported in ℚᵈ with rational masses...
3/4
3/4
... and (2) not UC for any p≥1 on the space of measures supported in (0,1) and (3) universally consistent for p=2 on the space of d-dimensional Gaussian measures.
Author: Donlapark Ponnoprat (@BomNaKub)
↳arxiv.org/abs/2009.04651
4/4
Author: Donlapark Ponnoprat (@BomNaKub)
↳arxiv.org/abs/2009.04651
4/4
• • •
Missing some Tweet in this thread? You can try to
force a refresh