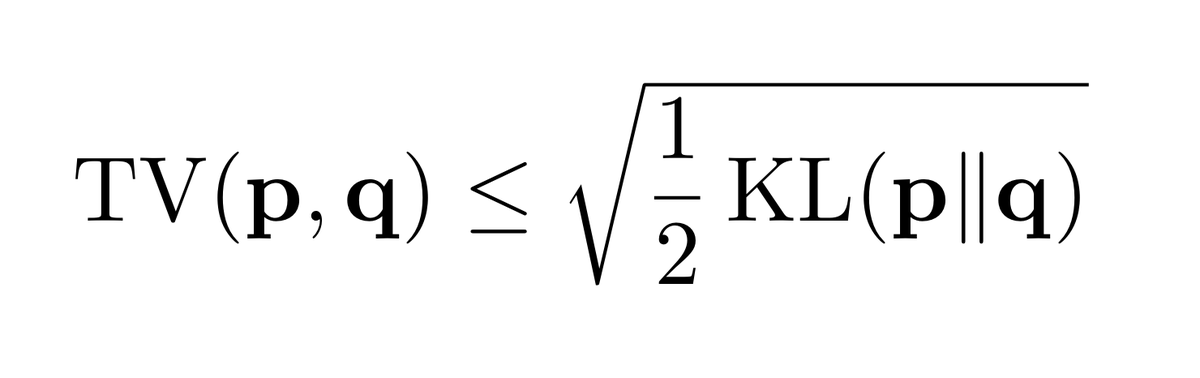Share this page!

Maybe Scrolly?
Clément Canonne Profile picture
Twitter logo
22 Aug, 13 tweets, 6 min read
📊 Answers and discussions for this week's we(a)ekly quiz on greedy algorithms.

Remember: greedy's only a sin if you *forget* to try it!

1/
Greedy #algorithms can be surprisingly powerful, on top of being very often quite intuitive and natural. (Of course, sometimes their *analysis* can be complicated... but hey, you do the analysis only once, but run the algo forever after!)

Let's have a look at a few examples.

2/
Q1 asked about which problem was *not* (known to) have an efficient, optimal greedy solution.

53.6% of you got it right: Set Cover. Well, one reason is because it's NP-hard, so that doesn't help (greedy or not)...
en.wikipedia.org/wiki/Set_cover…

3/
... on the other hand, the Greedy algo for Set Cover does achieve a (log n)-approximation ratio, which is... something? Also, something optimal, assuming P≠NP. So, even then: not so bad!
📝 pages.cs.wisc.edu/~shuchi/course… (PDF)

As for the others: Minimum Spanning Tree (MST) can...
4/
... be solved by Prim's or Kruskal's algorithms (both greedy), and Shortest Path (non-negative weights!) by Dijkstra's algorithm (greedy, too).

OK, let's look at another NP-Hard problem: Vertex Cover. "Given a graph G, gimme a small set of vertices covering every edge of G."
5/
19.6% of you answered Q2 correctly: that simple greedy algorithm doesn't solve VC exactly (hey, it's NP-Hard! 🧐), and does not provide a constant-factor approximation... bummer.

But it still provides a Θ(log n)-approx ratio. Not bad, still! And...

6/
... moreover, there *is* a 2-approximation possible via a greedy algorithm! (and no <1.36-approx unless P=NP).

Using a different greedy algo: one for maximal matching. But it counts! It's greedy! It's simple!

7/
At this point, I should have convinced that greed is good (if you weren't already).

But let's look at our 3rd question: Knapsack! Also NP-Hard, so it'll be about finding a "good enough" (approximation) solution.

BTW, I'd like to understand what's a knapsack (vs. backpack).

8/
So, the greedy algo for Knapsack (very natural: pick according to the ratio value-to-weight) can be arbitrarily bad, as 35.1% of you answered: ω(1)-approx. (Like, Ω(n)-bad 🤯).

Bummer. 😯

Bummer! 😞

But...! 🤔


9/
... there is a very, very simple fix to get a 2-approx! Just use the same Greedy algo. Just do it.

Then, at the end, return the best of TWO solutions: (1) what the Greedy algo returned, and (2) one item, "k+1,", the first Greedy refused to pick.

That's all. That's it.

10/
There is a lot of work on greedy algos, including understanding under which set of conditions they always lead to optimal solutions: matroid structures, etc.

Definitely worth looking into, if you're interested!

11/
 en.wikipedia.org/wiki/Greedy_al…
Also, many mentions (and an entire chapter) in Shmoys–Williamson's (excellent) book on approximation #algorithms: designofapproxalgs.com
(the website provides a free PDF version!)

12/
To conclude, I'll leave you with this open-ended Q, and the v. good answers *you* have provided to it: EM, Lloyd-max, Stable Marriage, Huffman coding, Kosaraju’s algo for strongly connected components, policy iteration, & more!

See you next week!

13/end

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Clément Canonne

Clément Canonne Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @ccanonne_

Clément Canonne Profile picture
23 Aug
My first foray into shuffle #privacy, spearheaded by my impressive winter research intern Hongyi Lyu (maths undergrad @UniMelb), who managed to learn about DP+shuffle DP+distribution testing, all this in ~6 weeks!

Comments welcome! 📝 arxiv.org/abs/2108.08987
1/4
This was part of the "Winter/Summer Research Internship" program at @Eng_IT_Sydney @Sydney_Uni:
sydney.edu.au/engineering/st…

Our (short) paper builds on|simplifies an algo of Balcer, Cheu, @mgtjoseph, & Mao. One key component of our analysis? This fact!


2/4
We also use the recent amplification theorem of @vitalyFM, McMillan, and @_kunal_talwar_ (local privacy to shuffle privacy) to provide an alternative algo:

3/4
Read 5 tweets
Clément Canonne Profile picture
21 Aug
Ninth #AcademicSpotlight: Donlapark Ponnoprat (@BomNaKub), Lecturer at @cmuofficial_tw

Paper: Universal Consistency of Wasserstein k-NN classifiers 📝
arxiv.org/abs/2009.04651

Pitch: understanding universal consistency of the k-NN classifier under Wasserstein distances!

1/4
In more detail: A binary classifier g(Dₙ) trained on dataset Dₙ is universally consistent (UC) if the error proba Pₓ,ᵧ(g(Dₙ)(X)≠Y|Dₙ) converges to the Bayes risk as n→∞, regardless of the joint distribution of X and Y. This paper studies the universal consistency...

2/4
... of the k-NN classifier on spaces of proba measures under p-Wasserstein distance. From studying geometric properties of Wasserstein spaces, we show that the k-NN classifier is (1) UC for any p≥1 on the space of measures finitely supported in ℚᵈ with rational masses...
3/4
Read 4 tweets
Clément Canonne Profile picture
30 Mar
Here is one:
If X has the same distribution as X', Y as Y', and Z as Z', do we have 𝔼[X+Y+Z]=𝔼[X'+Y'+Z']?
Note that this is true for only two r.v.'s: if X~X' and Y~Y'
𝔼[X+Y]=𝔼[X'+Y']
whenever 𝔼[X+Y] is defined (regardless of whether 𝔼[X] and 𝔼[Y] are defined). (cf. below from G. Simons (1977)).
Turns out, this fails for 3 r.v.'s (same paper by Simons, and Counterexample 6.1 in Stoyanov's book).

Sometimes 𝔼[X+Y+Z], 𝔼[X'+Y'+Z'] both exist, yet 𝔼[X+Y+Z]≠𝔼[X'+Y'+Z'].

(Again, for 2 r.v.'s the result holds: if 𝔼[X+Y], 𝔼[X'+Y'] both exist, then 𝔼[X+Y]=𝔼[X'+Y'].)
Read 5 tweets
Clément Canonne Profile picture
27 Mar
📊 Answers and discussions for this week's thread on distinguishing biased coins 🪙. Coin: it's like a die 🎲, but with two sides.

So the goal is, given a 🪙, to distinguish b/w it landing Heads w/ probability p or >p+ε, with as few flips as possible.

1/
Here, p and ε are known parameters (inputs), the goal is to be correct with probability at least 99/100 (over the random coin flips). As we will see, 99/100 is sort of arbitrary, any constant in 1/2 < c < 1 would work.

Also, warning: I'm going to give DETAILS.

2/
Let's start with Q1, the "fair" vs. ε-biased coin setting (p=1/2). As more than 66% of you answered, for Q1. the number of coin flips necessary and sufficient is then Θ(1/ε²). Why?

One way to think about it to gain intuition is "signal to noise."

3/
Read 32 tweets
Clément Canonne Profile picture
16 Dec 20
Stuff I wish I had known sooner: "Pinsker's inequality is cancelled," a thread. 🧵

If you want to relate total variation (TV) and Kullback-Leibler divergence (KL), then everyone, from textbooks to Google, will point you to Pinsker's inequality: TV(p,q) ≤ √(½ KL(p||q) )

1/
It's warranted: a great inequality, and tight in the regime where KL→0. Now, the issue is that KL is unbounded, while 0≤TV≤1 always, so the bound becomes vacuous when KL > 2. Oops.

2/
*I'm using it with the natural log, by the way, so no pesky log 2 constants.
This is annoying, because in many situations, you would want to bound a TV close to 1: for instance, in hypothesis testing: "how many samples to distinguish between an ε-biased and a fair coin, with probability 1-δ?"

Well, you'd like to start bounding 1-δ ≤ TV ≤ ?.

3/
Read 14 tweets
Clément Canonne Profile picture
4 Dec 20
📊 Answers and discussion for yesterday's quiz on sequences (and their names).

Before we go to the first question, again: if you haven't, bookmark oeis.org. It's useful: the solution to some of your problems may be recorded there!

1/
So, the first question... was a trap. All three answers were valid...

I was personally thinking of 203, since that corresponds to the next Bell number (en.wikipedia.org/wiki/Bell_numb…).

But maybe your were thinking of something else? Maybe the number of...

2/
... ascent sequences avoiding the pattern 201 (oeis.org/A202062)? Or the number of set partitions of [n] that avoid 3-crossings (oeis.org/A108304)? Who am I to judge?

(I prefer Bell numbers.)

3/
Read 10 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Too expensive? Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal Become our Patreon

Thank you for your support!

Follow Us on Twitter!

Like this author's thread?

Get emails when @ccanonne_ has new unrolls!

Check out other threads from @ccanonne_!

Read all threads by @ccanonne_

:(