Share this page!

Enter URL or ID to Unroll

You can paste full URL like: https://x.com/threadreaderapp/status/1644127596119195649
or just the ID like: 1644127596119195649

How to get URL link on X (Twitter) App

  1. On the Twitter thread, click on or icon on the bottom
  2. Click again on or Share Via icon
  3. Click on Copy Link to Tweet
  4. Paste it above and click "Unroll Thread"!
  5. More info at Twitter Help
Rosana Ferrero 📈📊🙌 Profile picture
@RosanaFerrero
Oct 30, 2022 • 7 tweets • 11 min read • Read on X
Scrolly
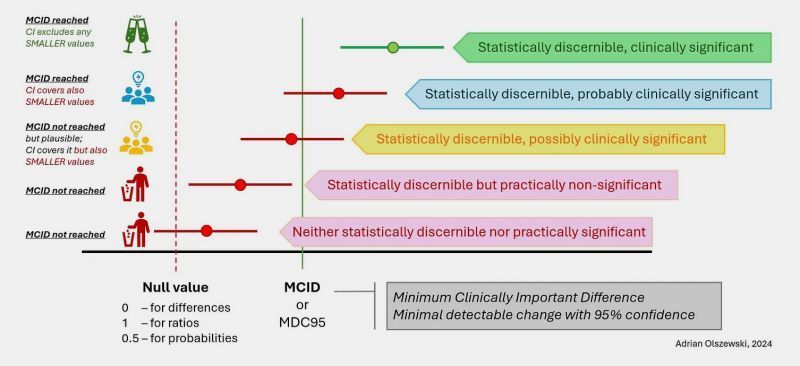
ERRORES QUE DAN MIEDO👻en #DataScience🎃
📊"Una imagen vale más que mil palabras", o que mil datos. Los gráficos cuentan la historia de los datos, nos ayudan a guiar, interpretar y comunicar😉
Cuidado con estos #HorrorStats
#HappyHalloween #Halloween #FelizDomingo #HalloweenEnds
🚫1. Elegir el gráfico incorrecto💀

Cada gráfico tiene sus propios casos de uso. ¿Tiene sentido representar el crédito € de una tarjeta con un gráfico de sectores? 🤌

#HorrorStats #HappyHalloween～ #trickortreat #DataScience #dataviz #DataScience #data
¿Qué gráfico utilizar?👇
🚫2. Manipular los ejes del gráfico💀

👉Distorsionar la escala, truncarla u omitir líneas de base es un error, intencionado o no.🤦🏻‍♀️

¿Quieres más ejemplos?👇

#HorrorStats #HappyHalloween～ #trickortreat #DataScience #dataviz #RStats #Python #DataVisualization #Stats #Analytics
🚫3. Eliminar datos atípicos del gráfico.😱

👨‍💻Si un gráfico parece que recorta algunos de los datos, no es confiable. Los valores atípicos (outliers) también deben representarse.👻

¿Qué son los "outliers"? 👇maximaformacion.es/blog-dat/como-…

#HorrorStats #HappyHalloween #DataScience #ML
🚫4. No evaluar los supuestos del modelo y su ajuste mediante gráficos.🎃

El Cuarteto de Anscombe: 4 conjuntos de datos con misma media, var, correlación, línea de regresión, etc. pero ¿En cuál tiene sentido ajustar una regresión lineal?😱👇
maximaformacion.es/blog-dat/error…

#HorrorStats
🚫5. Utilizar datos incorrectos🤦🏻‍♀️

🗑"Basura entra, basura sale". En el contexto de los gráficos esto significa que los datos incorrectos darán lugar a visualizaciones incorrectas.💀

#HorrorStats #HappyHalloween～ #dataviz #FelizDomingoParaTodos #DataScience #HalloweenEnds #ML
¿Conoces algún ejemplo famoso con errores en sus gráficos? Te leo😉

🚀Si te quedaste con ganas de más descarga nuestro recurso gratuito ¡IMPRESIONA CON TUS GRÁFICOS! maximaformacion.es/wp-content/upl…
Mañana otra serie ESCALOFRIANTE QUE DA MIEDO en #DataScience #HorrorStats #HappyHalloween

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Rosana Ferrero 📈📊🙌

Rosana Ferrero 📈📊🙌 Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @RosanaFerrero

Rosana Ferrero 📈📊🙌 Profile picture
Feb 10
𝑽𝒂𝒓𝒊𝒂𝒃𝒍𝒆𝒔 𝒅𝒆 𝑪𝒐𝒏𝒇𝒖𝒔𝒊ó𝒏: riesgos, límites y consideraciones críticas👇🧵
¿Qué es un confusor? ¿Cuáles son sus consecuencias?
¿Cómo evitar problemas de confusores? ¿Qué limitaciones debemos tener en cuenta?

#stats #datascience #master #analytics #cienciadedatos Image
¿Qué es? Una variable de confusión (o confusor) es un tercer factor que cambia la asociación entre otras 2 variables: la exposición (e.g. el factor de riesgo que se estudia) y el resultado (e.g. el efecto en la salud).

3 condiciones👇 Image
¿Consecuencias? El efecto real de la exposición se mezcla con el efecto de otros factores que también influyen en el resultado, dificultando la identificación de la verdadera relación causal.

Puede alterar los resultados en magnitud o dirección.

#datascience #master #analytics Image
Read 7 tweets
Rosana Ferrero 📈📊🙌 Profile picture
Feb 4
🚨𝐏𝐨𝐭𝐞𝐧𝐜𝐢𝐚 𝐞𝐬𝐭𝐚𝐝𝐢𝐬𝐭𝐢𝐜𝐚: 𝐧𝐨 𝐥𝐨 𝐩𝐥𝐚𝐧𝐢𝐟𝐢𝐪𝐮𝐞𝐬 𝐩𝐚𝐫𝐚 𝐥𝐨 𝐪𝐮𝐞 𝐞𝐬𝐩𝐞𝐫𝐚𝐬, 𝐩𝐥𝐚𝐧𝐢𝐟𝐢𝐜𝐚́𝐥𝐚 𝐩𝐚𝐫𝐚 𝐥𝐨 𝐪𝐮𝐞 𝐧𝐨 𝐪𝐮𝐢𝐞𝐫𝐞𝐬 𝐩𝐚𝐬𝐚𝐫 𝐩𝐨𝐫 𝐚𝐥𝐭𝐨
Te cuento por qué👇🧵

#stats #datascience #analytics #dataanalysis Image
𝐋𝐚 𝐩𝐨𝐭𝐞𝐧𝐜𝐢𝐚 𝐞𝐬𝐭𝐚𝐝𝐢𝐬𝐭𝐢𝐜𝐚 es 1−β: la probabilidad de evitar un 𝐞𝐫𝐫𝐨𝐫 𝐝𝐞 𝐭𝐢𝐩𝐨 II, es decir, de no pasar por alto un efecto real del tamaño especificado. Una potencia baja implica un alto riesgo de concluir que no hay efecto cuando sí existe.
#master Image
Por eso, el enfoque correcto no es basarse en el efecto esperado, sino en el 𝐭𝐚𝐦𝐚𝐧̃𝐨 𝐝𝐞𝐥 𝐞𝐟𝐞𝐜𝐭𝐨 𝐝𝐞 𝐢𝐧𝐭𝐞́𝐫𝐞𝐬 𝐦𝐚́s 𝐩𝐞𝐪𝐮𝐞𝐧̃𝐨 (𝐒𝐄𝐒𝐎𝐈). Esto define el umbral de relevancia científica o práctica que no queremos pasar por alto.
#cienciadedatos #phd Image
Read 6 tweets
Rosana Ferrero 📈📊🙌 Profile picture
Jan 30
😱 ¿Tienes varias mediciones de un mismo sujeto, sensor o ciudad? ¡Cuidado! Tratarlas como si fueran observaciones independientes (e.g. tratar 25 mediciones de 5 sujetos como si fueran 25 sujetos distintos) es cometer pseudoreplicación. Y este error invalida tus conclusiones:👇🧵 Image
1️⃣Inferencia
Al ignorar la dependencia, el modelo asume que cada dato aporta información nueva y única. Esto subestima el error estándar e infla los estadísticos de prueba.
Consecuencia: Aumentan los falsos positivos y se distorsionan artificialmente los intervalos de confianza.
2️⃣ Estimación de Efectos (Intra vs. Inter)
Impide distinguir entre la variabilidad intra-sujetos (cambios en el tiempo) y inter-sujetos (diferencias inherentes).
Consecuencia: Los efectos aparentan ser más precisos de lo que realmente son, y puedes caer en la Paradoja de Simpson.
Read 9 tweets
Rosana Ferrero 📈📊🙌 Profile picture
Jan 25
⚽ En este post tienes una introducción divulgativa y práctica al papel del data scientist en el fútbol, explicando qué datos se generan, cómo se analizan y para qué se usan en la toma de decisiones deportivas.


#stats #datascience #ML #LaLiga #dataviz maximaformacion.es/blog-ciencia-d…Image
Hoy cada partido y entrenamiento producen una avalancha de información que ya no se puede gestionar solo con intuición.
El data scientist entra en escena para responder preguntas que antes no tenían respuesta clara:

#MachineLearning #EstadísticaDeportivo #InnovaciónDeportiva Image
El fútbol sigue siendo emocional. Pero la toma de decisiones ya no lo es tanto.
Cada vez más clubes (grandes y pequeños) tienen equipos internos de datos. Porque decidir fichajes, rotaciones o planteamientos sin datos hoy es asumir desventaja estructural.

#AnálisisDeDatos Image
Image
Image
Read 4 tweets
Rosana Ferrero 📈📊🙌 Profile picture
Jan 22
🚨𝗖𝗼́𝗺𝗼 𝗲𝘃𝗮𝗹𝘂𝗮𝗿 𝘂𝗻 𝗺𝗼𝗱𝗲𝗹𝗼 𝗽𝗿𝗲𝗱𝗶𝗰𝘁𝗶𝘃𝗼: decenas de métricas... y mucha confusión
La evaluación de modelos predictivos está plagada de métricas (¡existen más de 30!), pero ¿Qué preguntas responden realmente?

𝟱 𝗱𝗶𝗺𝗲𝗻𝘀𝗶𝗼𝗻𝗲𝘀 conceptuales👇🧵 Image
👉 Si no distingues estos dominios, estás evaluando mal el modelo, aunque los números “salgan bien”.

Artículo:

#stats #analytics #Estadística #DataScience #ModelosPredictivos #IA #ML hal.science/hal-04841858v1…Image
👀 Interpretación de cada dimensión (y sus peligros) Image
Read 5 tweets
Rosana Ferrero 📈📊🙌 Profile picture
Jan 21
𝗨𝗡𝗔 𝗠𝗔𝗧𝗥𝗜𝗭 𝗗𝗘 𝗖𝗢𝗡𝗙𝗨𝗦𝗜𝗢́𝗡 𝗡𝗢 𝗦𝗜𝗥𝗩𝗘 𝗣𝗔𝗥𝗔 “𝗩𝗘𝗥 𝗦𝗜 𝗘𝗟 𝗠𝗢𝗗𝗘𝗟𝗢 𝗔𝗖𝗜𝗘𝗥𝗧𝗔 𝗠𝗨𝗖𝗛𝗢”,
𝗦𝗜𝗡𝗢 𝗣𝗔𝗥𝗔 𝗘𝗡𝗧𝗘𝗡𝗗𝗘𝗥 𝗖𝗢́𝗠𝗢 𝗦𝗘 𝗘𝗤𝗨𝗜𝗩𝗢𝗖𝗔.

¿Cómo evaluar qué errores comete, con qué frecuencia y a qué coste?

#stats Image
▶︎ 𝗘𝗫𝗔𝗖𝗧𝗜𝗧𝗨𝗗 (𝗔𝗖𝗖𝗨𝗥𝗔𝗖𝗬)
Porcentaje total de aciertos.
⚠️ Si una clase es mayoritaria, un modelo trivial que siempre predice esa clase puede tener una exactitud alta sin capacidad predictiva real.

Debes superar la tasa de no información (% clase mayoritaria)
▶︎ 𝗦𝗲𝗻𝘀𝗶𝗯𝗶𝗹𝗶𝗱𝗮𝗱 (𝗥𝗲𝗰𝗮𝗹𝗹, 𝗧𝗣𝗥)
Capacidad de detectar positivos reales.
Penaliza falsos negativos.

▶︎ 𝗘𝘀𝗽𝗲𝗰𝗶𝗳𝗶𝗰𝗶𝗱𝗮𝗱 (𝗧𝗡𝗥)
Capacidad de identificar negativos reales.
Penaliza falsos positivos.

Optimizar una suele empeorar la otra.
Read 10 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Don't want to be a Premium member but still want to support us?

Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal

Or Donate anonymously using crypto!

Ethereum

0xfe58350B80634f60Fa6Dc149a72b4DFbc17D341E copy

Bitcoin

3ATGMxNzCUFzxpMCHL5sWSt4DVtS8UqXpi copy

Thank you for your support!

Follow Us!

Send Email!

:(