Thread by @wsosaescudero

Hoy en #estadisticaXtuiter Que cuernos significa que un estimador sea sesgado? Incluye tutorial en R al final!!!!!

Pensa: Periodista sesgado? Profesor sesgado? Argumento sesgado? Spoiler: insesgado = justo. Que no favorece nada que no sea la verdad.

Mira este dibujo. 25 puntos y la recta de regresión estimada por minimos cuadrados (MCO). Es posible ver gráficamente que MCO es insesgado? Maestro, redoble, por favor….. No, no se puede. Que?

Lo que te estoy mostrando (la recta) es una ESTIMACION, que surge de meterle datos a un ESTIMADOR. La propiedad de ser insesgado es del estimador, no de la estimación, no te confundas.

Estimador? Formula, que si le pones datos, escupe una estimación

Un estimador es una variable aleatoria. Por que? Porque “come” datos, que son a su vez aleatorios. Una estimación es una realización de una variable aleatoria, capisce?

Un estimador es insesgado si en promedio da el verdadero valor que se pretende estimar. Ahora… ¿en promedio de que? Eh? De los distintos datos que podrian haber aparecido! Que? Como? Esto es lo difícil de entender, ahí vamos.

Los 25 puntos que te mostre en el grafico son los datos, que usamos para construir la recta por MCO. Que habría pasado si en vez de haber usado esos 25 datos, hubiésemos observados otros 25 datos, pero de la misma población de referencia?

Respuesta: si el estimador es insesgado, no deberíamos esperar que la recta cambie.

Te propongo un experimento. Supongamos que “la población” consiste en los 200 puntos que te muestro, y que la verdadera recta de regresión es la que se corresponde con esos 200 puntos. Ahí te la muestro.

Pero ahora suponte que para estimar solo te permito usar 25 puntos elegidos al azar, de esos 200 que te mostre. Y que a 99 personas les damos otros 25 puntos al azar. Al terminar el experimento, tendremos 100 estimaciones, en base a 25 datos cada una.

Ahora tenes que pensar: en términos del experimento anterior, que significa que MCO sea insesgado? Ahí te muestro los 200 puntos originales, la recta “verdadera” (en negro) y las 100 estimaciones con 25 datos cada una (en rojo).

Insesgado: en promedio las rectas en rojo (muestrales) aciertan a la recta en negro (poblacional). La recta poblacional (negra) es y=0.7+1X y el promedio de las rectas da Y=0.69+1.01 X. Magia? No, matemática!

En la practica la naturaleza solo te regala UNO de los datasets. Entonces, para que me sirve saber que el estimador es insesgado?

Respuesta: como de antemano no sabes que dataset te tocara, si el estimador es insesgado, no favorece ninguna recta roja en particular.

Insesgado: propiedad de la formula, no de lo que sale de la formula. Ejemplo: si se trata de un rifle, la propiedad de ser insesgado es del rifle, no de los disparos.

Un disparo no puede ser insesgado. Para ver si el rifle es insesgado, hay que disparar muchas veces y ver que en promedio da en el centro. ¿Para que me sirve esto si voy a disparar una vez?: ante la incertidumbre, si el rifle es insesgado deberías apostar a que de en el centro.

Insesgadez: ante la incertidumbre, el estimador es “justo”. Para que sea “preciso” tenemos que hablar de la varianza. Ese es otro #estadisticaXtuiter

Enseñanza clave: Para ver si el estimador es insesgado hay que estudiar la FORMULA, no se puede ver si el estimador es insesgado viendo una salida de regresión! Nada mas útil que una buena teoría.

Te dejo una pregunta: es hiperimportante que un estimador sea insesgado? No, pensalo bien, discutiremos esto en otro #estadisticaXtuiter

Y ahora viene un tutorial en R!! Empezamos creando un modelo poblacional, que generara la “verdadera” recta de regresion

x<-runif(200)*10
u<-rnorm(200)*1.5
y<-1+x+u
plot(x,y)
modelo<-lm(y~x)
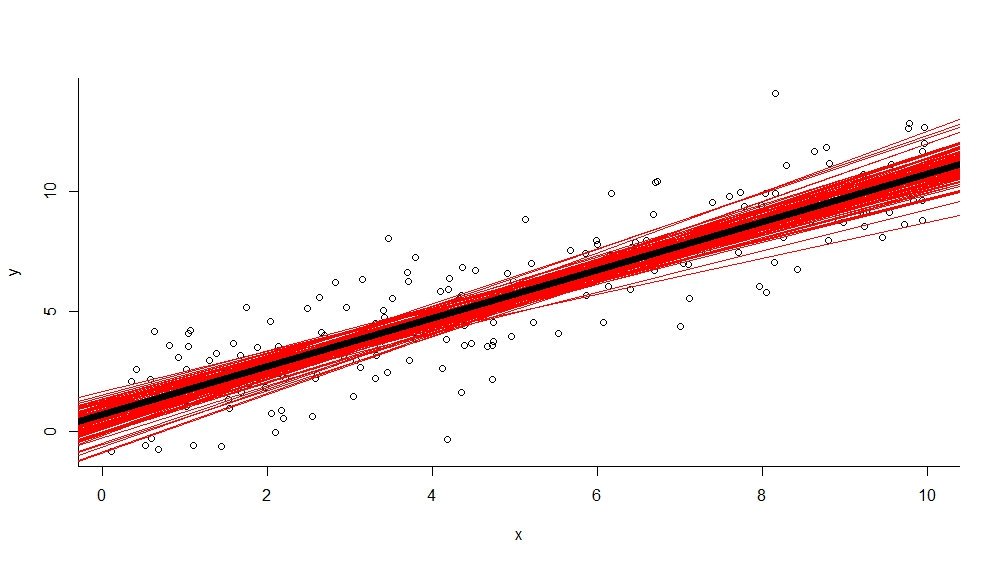
abline(modelo, lwd=5)
summary(modelo)

Experimento: estimamos 100 veces, con 25 datos elegidos al azar

B<-100; N<-25
coefs<-matrix(rep(0,B*2), B,2)
for(i in 1:B){
pick<-sample(1:length(x),N)
models<-lm(y[pick]~x[pick])
coefs[i,]<-models$coefficients
abline(models, col="red")
}
abline(modelo, lwd=5)

Acá los 100 pares de coeficientes estimados, el promedio y los que poblacionales

round(coefs,3)
colMeans(coefs)

Ahi tenes insesgado: el promedio de las 100 estimaciones con 25 datos da los valores poblacionales

Mama, mama, y en Python? Como se decía en casa cuando venían visitas “te dejo la puerta entornada, para que puedas entrar con el paquete”

Ejercicios
1.Que pasa si cambias B o N?
2.Hace el experimento.
3.Modifica todo lo que te plazca, comparti tus resultados

Creditos: basado en un iluminador tuit de @_lacion_ y en algo que le vi hacer al fenómeno de @MartinGRozada

@_lacion_ @MartinGRozada Ahora si, me congratulo y me repercuto. Gracias por la buena onda.

@_lacion_ @MartinGRozada Coda: algun dia hare la version bayesiana de este hilo. Afortunadamente, no es muy distinta