Thread by @Manuj_Hidalgo

Os explico por qué es importantísimo tener en cuenta el llamado EFECTO COMPOSICIÓN en el debate público o en el diseño de políticas. Uso un ejemplo para ayudar a entenderlo: las diferencias salariales entre trabajadores públicos y privados.
Abro hilo:

Supongamos que leemos que los trabajadores en el sector público ganan más que en el privado. Una primera lectura, sobre todo si te dominan sesgos ideológicos que te hacen pensar que todo lo público es “caca”, es que es injusto y que hay que acabar con ello.

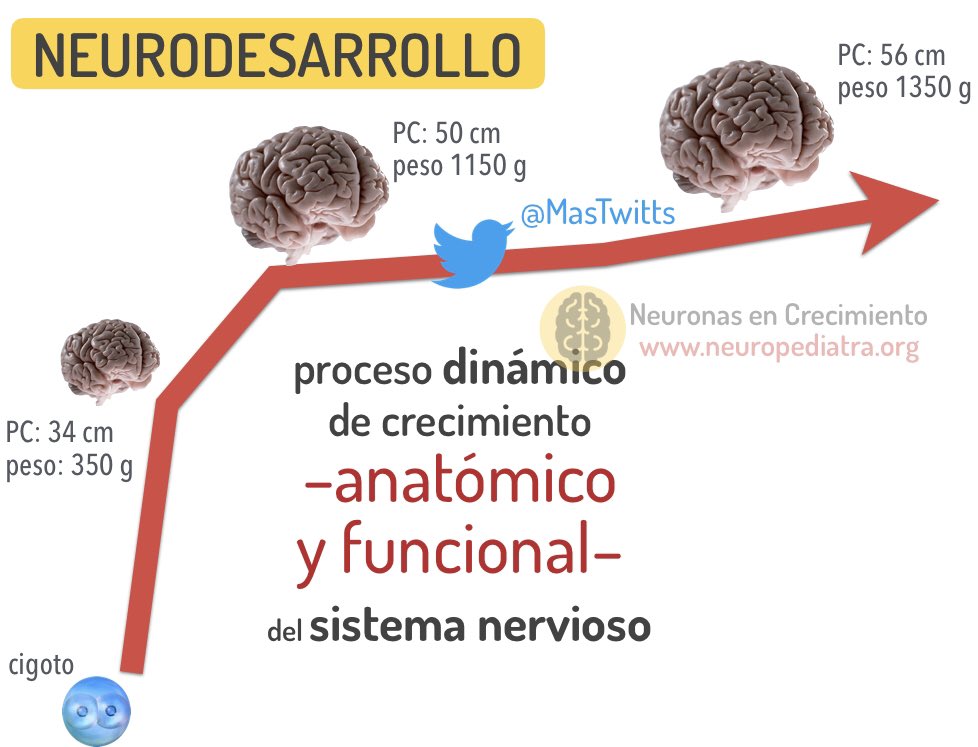
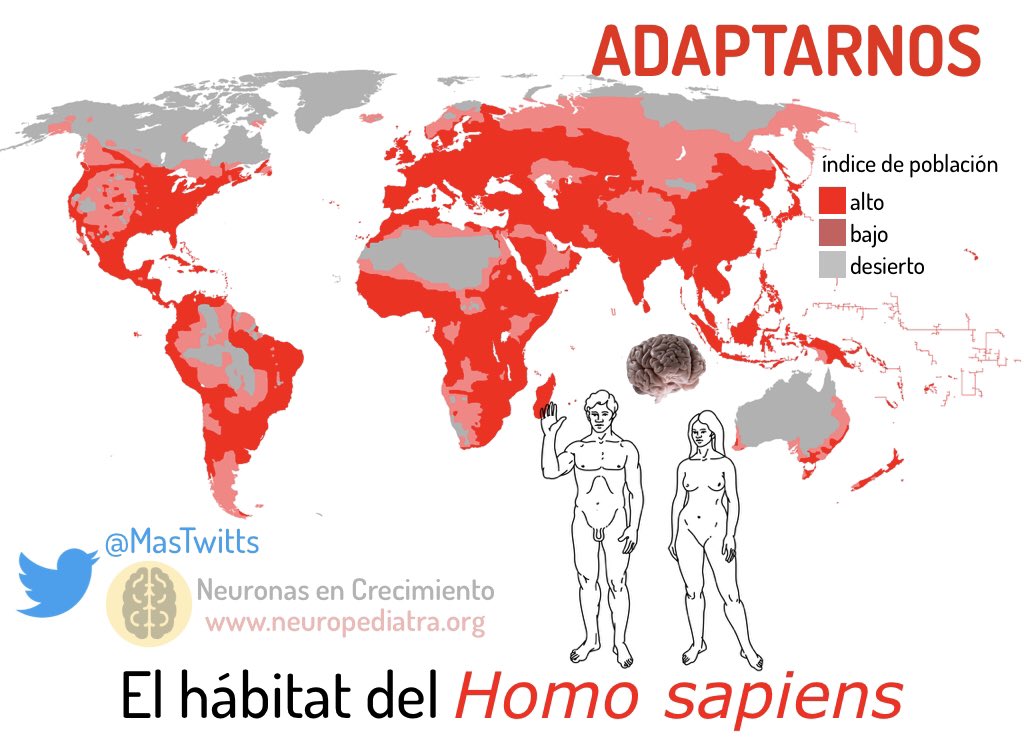
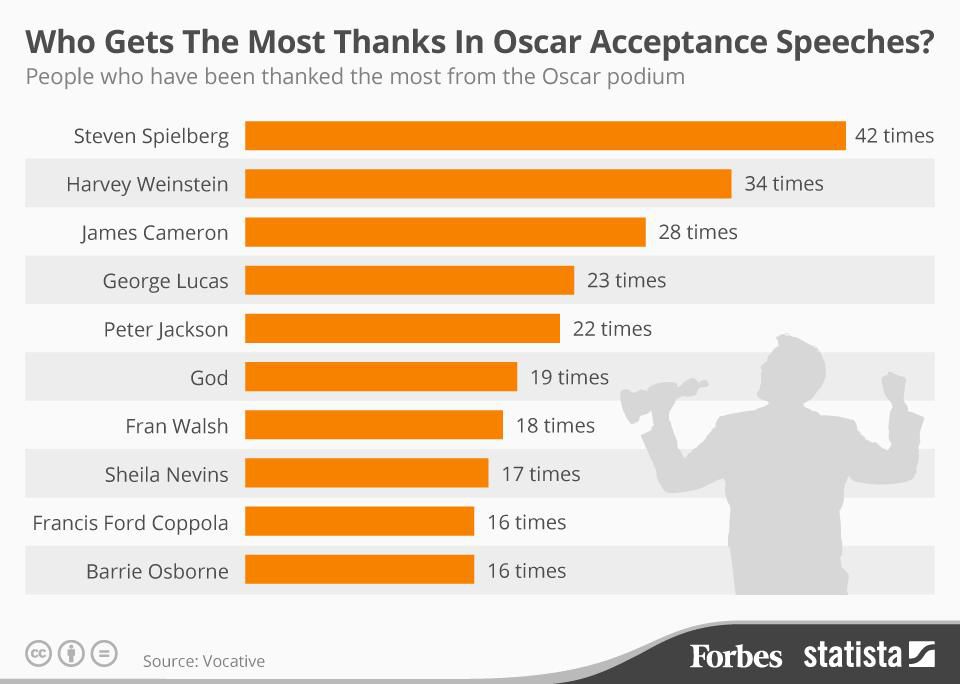
Pero un análisis lógico (¡ay, la lógica!) puede hacerte cambiar de opinión (o no,
dependiendo de lo arraigado que tengas esos prejuicios).
Prejuicio y lógica no se llevan bien.

Pongo mates. No las uso para demostrar nada, SOLO para ayudar al desarrollo de lo que quiero explicar.

Agarraos: Supongamos que X es el salario medio de un empleado público e Y el del sector privado.
Afirmamos que X>Y.
Ojo, aquí “medio” es lo relevante, algo que habitualmente no es tenido en cuenta en los análisis periodísticos ni en las conversaciones de café.

Pues bien, supongamos que podemos expresar que el salario medio de un empleado público viene explicado por una serie de características de estos trabajadores y cómo se remuneran estas. Matemáticamente, simplificando a una representación lineal, tendremos que:

X=Sum(i)[b(i)x(i)]
Os lo explico. Sum viene a decir que estamos sumando cosas. Esas cosas son varias (hay i diferentes) y cada una, x(i), representa a una característica media del trabajador. b(i) es el pago por esa característica.

Por ejemplo, supongamos que las características que explican el salario de un empleado público son dos, x(1) y x(2). En ese caso:
X=b(1)x(1) + b(2)x(2)
En la forma anterior i llega hasta 2. Asumimos que hay un i muy elevado, por lo que hay muchas características que explican X

En este caso, x(1) es la media para empleados públicos de la característica 1. Por ejemplo, años medios de estudio. x(2) podría ser el número medio de años de experiencia.
Así, el salario medio de un empleado público se explica tanto por su valor medio de las características

como por el pago o retorno a esas características.
En este caso, b(1) sería cuánto remunero un año más de estudios.
Cuanto más años de estudio o más años de experiencia, mayor salario si las b>0.

Igualmente, Y podría expresarse como
Y=c(1)y(1) + c(2)y(2)

Por ello, podríamos decir que X e Y son diferentes porque:
- las características que los explican difieren entre sí (x e y’s). Diferentes medias.
- y/o los pagos por dichas características difieren entre sí (b y c’s)

Inventemos ahora un contrafactual.
¿Cuánto ganaría un empleado público medio si dadas sus características medias observadas obtuviera un pago a cada una de ellas similar al privado.

Pues ese salario medio sería:

X’=c(1)x(1) + c(2)x(2)

Guardemos esta expresión.

Vamos ahora a explicar la diferencia en salario medio que es lo que nos interesa:

X-Y= b(1)x(1) + b(2)x(2)-
-c(1)y(1) - c(2)y(2)

Hagamos un truquito. Sumemos y restemos el contrafactual. Si lo hacemos, entonces tenemos:

X-Y= b(1)x(1) + b(2)x(2)-
-c(1)x(1) - c(2)x(2)+
+c(1)x(1) + c(2)x(2)-
-c(1)y(1) - c(2)y(2)

Como entenderéis, la igualdad no cambia al sumar y restar lo mismo.

Reordenando, tenemos

X-Y= {b(1)-c(1)}x(1) +
+{b(2)-c(2)}x(2)+

+c(1){x(1)-y(1)} +
+c(2){x(2)-y(2)}

Vamos por partes

{b(1)-c(1)}x(1) + {b(2)-c(2)}x(2) representa la parte de la diferencia entre X e Y explicada por pagos diferentes a similares características.
Mirad cómo lo que está entre {} es la diferencia de los pagos por años de estudio o experiencia. Es por ello que esta parte

mide algo parecido a lo que en algunos casos llamamos discriminación. Explicando la segunda parte, lo entenderemos mejor.

c(1){x(1)-y(1)}+ c(2){x(2)-y(2)} es la parte de la diferencia de las medias X e Y explicada por diferentes dotaciones medias de características.

Fijaros como multiplicamos por mismo retorno. Pero este multiplica a medias de años de estudio o experiencia diferentes. Por ello esta parte explica la diferencia entre X y Y que viene determinada por diferentes dotaciones o características. Es lo que llamamos EFECTO COMPOSICIÓN.

Si los dos grupos de trabajadores tienen mismas medias en años de estudio y experiencia, no hay efecto composición, y la diferencia entre X y Y vendría por la primera parte: pagos diferentes a similares características. En algunos casos a esto lo llamamos DISCRIMINACIÓN.

Resumiendo: las diferencias salariales en estos dos grupos se explican por la existencia de un efecto discriminación (diferente pago a iguales) y un efecto composición (diferente pago por ser diferentes colectivos).

Y ahora pensad. Este análisis puede aplicarse a cualquier diferencias de medias (se usa mucho para analizar las diferencias por género en salarios medios), pero también en probabilidades o en percentiles. También en otros estadísticos, como varianzas, etc

Y ahora busquemos en qué nos puede ayudar estos análisis.
Supongamos q queremos reducir la brecha salarial de género. Os sorprendería saber que según qué parte sea más potente, la medida a aplicar sería diferente.
Xej, la discriminacion puede reducirse mediante medidas legales.

Entre otras, la de composición, en gran parte debida a segregación, con políticas de otro tipo.
El común de los mortales, en casi todos los casos, suele creer que X-Y se explica siempre SOLO por la discriminación. Sin embargo, el efecto composición es muy importante por lo

general.
Y claro, cuando hay sesgos hacia creer esto, las políticas a aplicar son insuficientes por no decir erróneas.
Aplicad esto a cualquier diferencia entre colectivos que queráis analizar:
- diferentes resultados escolares
- probabilidad de fracaso escolar

- intensidad en la I+D+i por países o regiones
- diferencias en productividad

o, finalmente,
- diferencias en el acceso a ayudas sociales en función de la nacionalidad

Espero este hilo os ayude a eliminar en el futuro algún sesgo o, incluso, prejuicio. Que os ayude a ser críticos con aquello que oís o leéis.
Saludos y buen domingo.

Fin