Share this page!

Liuto Giusto Profile picture
Twitter logo
29 Nov, 8 tweets, 3 min read
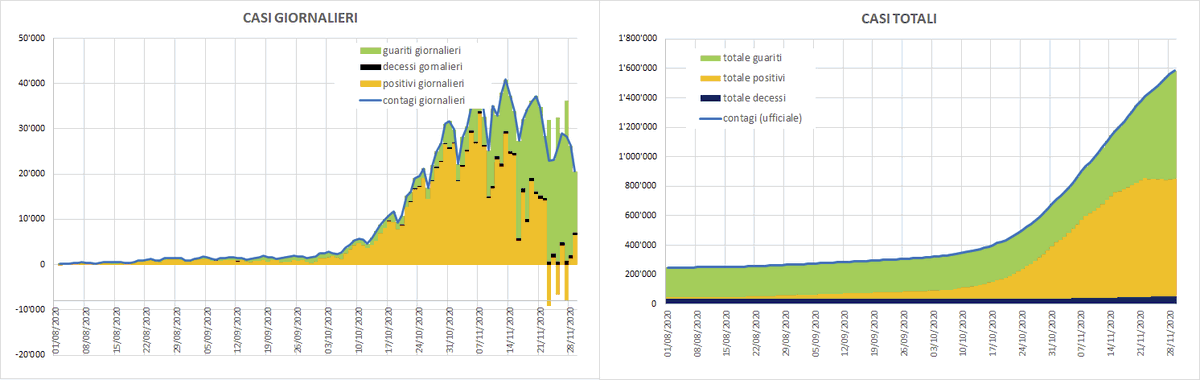
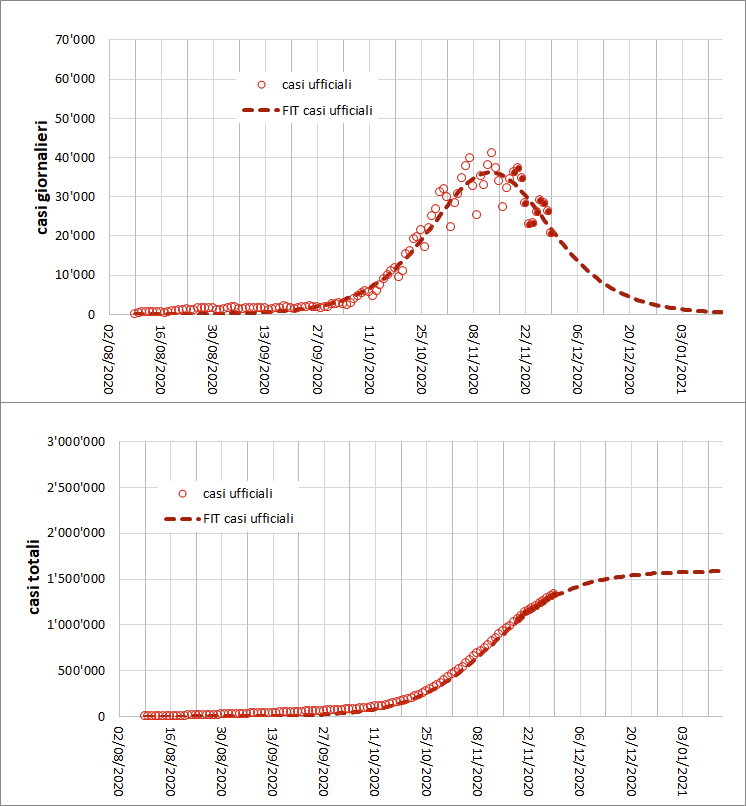
AGGIORNAMENTO COVID ITALIA - SI SCENDE

il modello è quasi invariato rispetto a quello del 18 Novembre

#coronavirus
#coronavirusitalia

1/8
Dati ufficiali

2/8
Casi ufficiali (sottostimati, si sa)

3/8
Casi plausibili

4/8
Decessi
Si arriverà a febbraio a 30.000 decessi (contati dal 01/08) ai quali vanno sommati i 35.000 della prima ondata, per un totale di 65.000

5/8
Tassi di crescita dei dati cumulativi (totale al giorno n/totale al giorno n-1)
6/8
Diagramma logaritmico casi ufficiali e decessi
7/8
Tamponi
8/8

• • •

Missing some Tweet in this thread? You can try to force a refresh
　

Keep Current with Liuto Giusto

Liuto Giusto Profile picture

Stay in touch and get notified when new unrolls are available from this author!

Read all threads

This Thread may be Removed Anytime!

PDF

Twitter may remove this content at anytime! Save it as PDF for later use!

Try unrolling a thread yourself!

how to unroll video
  1. Follow @ThreadReaderApp to mention us!

  2. From a Twitter thread mention us with a keyword "unroll"
@threadreaderapp unroll

Practice here first or read more on our help page!

More from @LiutoGiusto

Liuto Giusto Profile picture
18 Nov
SECONDA ONDATA: SI SCENDE
(iso-restrizioni, ahinoi..)
(thread)
#coronavirus
#coronavirusitalIa
1/10
Tutti gli indicatori dicono che dovremmo cominciare la discesa. Guardiamo i casi ufficiali:
2/10
ora un'occhiata ai tassi di crescita, ovvero il rapporto tra il dato comulato in un giorno e quello del giorno precedente. Qui si nota bene che l'unico dato che non è ancora in piena discesa è quello dei decessi.
3/10
Read 12 tweets
Liuto Giusto Profile picture
22 Oct
Ho messo mano ai dati e aggiornato il modello
#Covid_19
#COVID19italia
(thread)
1/13
primo assunto: bisogna ripartire da zero senza considerare la prima ondata. Perchè le malattie stagionali sono come delle onde, delle sinusoidi.
Siccome i dati più certi che abbiamo a disposizione sono (ahinoi) i decessi

2/13
ho preso come momento di inizio della seconda ondata il periodo in cui si è verificato il minimo dei decessi, intorno al 15/08. Quindi occhio: i dati cumulativi vengono considerati a partire da questa data.

3/13
Read 14 tweets
Liuto Giusto Profile picture
28 Aug
+++THREAD+++
I dati ci dicono tante cose, basta saperli leggere:
- i contagi ufficiali crescono ma i decessi no. Perchè?
- il lockdown è servito?
1/14

#COVIDー19
Ho aggiornato il modello matematico che usavo durante l'emergenza per prevedere l'andamento dei contagi e dei decessi. Ho interpolato una "funzione logistica" tra i dati ufficiali del periodo di lockdown: dal 20/03 (momento di picco) al 18/05 (fine lockdown)
2/14
Questo equivale a prevedere come si sarebbe sviluppata la pandemia in italia se fossimo rimasti chiusi in casa come durante il lockdown. E' come se il 18/05 avessi provato a prevedere l'evolvere dei contagi e dei decessi futuri.
3/14
Read 14 tweets
Liuto Giusto Profile picture
13 Apr
Secondo me il valore di R0 è più alto di 2.5.
Si attesta intorno a 5.7.
(THREAD)
(1)
#coronavirus
#COVIDー19
#COVID2019
#COVID2019italia
R0 è il numero di persone che ciascun contagiato infetta. Per fare questo impiega mediamente un tempo che chiamamamo "i". Se nel giorno (x) abbiamo N(x) contagiati, dopo "i" giorni avremo un numero di contagiati pari quelli del giorno (x) moltiplicati per (R0+1)
(2)
in notazione matematica:

N(x+i)=N(x)*(1+R0)

Nella fase esponenziale, i contagiati di ogni giorno sono ottenibili come quelli del giorno precedente moltiplicati per un valore costante K. Vi ricordate che all'inzio ogni giorno si aggiungevano 34% di contagiati in più?
(3)
Read 8 tweets
Liuto Giusto Profile picture
11 Apr
Aggiorno la stima dell'ingresso del primo caso in italia. Prendiamo il periodo in cui il tasso di moltiplicazione giornaliera è ancora costante (ante 12/03), pari a 1.34. Questo è una buona stima del tasso naturale di moltiplicazione dei decessi (e quindi degli infetti).
(1/6)
Se è vero che R0=2.5 come stimato da molti, si può anche stimare in quanto tempo mediamente un infetto ne contagia altri 2.5: in fase esponenziale il fattore moltiplicativo giornaliero dei casi è K=(1+R0)^(1/tempo di infezione)---->tempo infezione=ln(R0+1)/lnK
(2/6)
tempo infezione=ln(R0+1)/lnK=ln(2.5+1)/ln(1.34)=4.3giorni
quindi se ogni positivo ne infetta altri 2.5, impiega mediamente 4.3 giorni per farlo. Questo da anche un'idea della velocità di diffusione del virus, cosa che R0 da solo non da
(3/6)
Read 6 tweets
Liuto Giusto Profile picture
31 Mar
THREAD
Analisi casi #COVID2019 per regioni
#COVID19italia
#coronavirus
#COVID19
sono incappato in questo video molto interessante su un modo efficace di visualizzare l'evolversi dell'epidemia in un grafico bi-logaritmico


#COVID19italia
#coronavirus
#COVID19
In sostanza si plottano i casi totali in funzione di quelli giornalieri, ciascuno in scala logaritmica. Durante l'evoluzione esponenziale il grafico si muove su una retta. Quando l'epidemia rallenta i dati si allontanano a destra della retta

#COVID19italia
Read 24 tweets

Did Thread Reader help you today?

Support us! We are indie developers!

This site is made by just two indie developers on a laptop doing marketing, support and development! Read more about the story.

Become a Premium Member ($3/month or $30/year) and get exclusive features!

Become Premium

Too expensive? Make a small donation by buying us coffee ($5) or help with server cost ($10)

Donate via Paypal Become our Patreon

Thank you for your support!

Follow Us on Twitter!

Like this author's thread?

Get email notifications when new thread is out from this Author!

Check out other threads from this Author!

Read all threads by @LiutoGiusto