— Context —
Speaking about the transformer architecture, one may incorrectly talk about an encoder-decoder architecture. But this is *clearly* not the case.
The transformer architecture is an example of encoder-predictor-decoder architecture, or a conditional language-model.
Speaking about the transformer architecture, one may incorrectly talk about an encoder-decoder architecture. But this is *clearly* not the case.
The transformer architecture is an example of encoder-predictor-decoder architecture, or a conditional language-model.
https://twitter.com/alfcnz/status/1380181503112527876

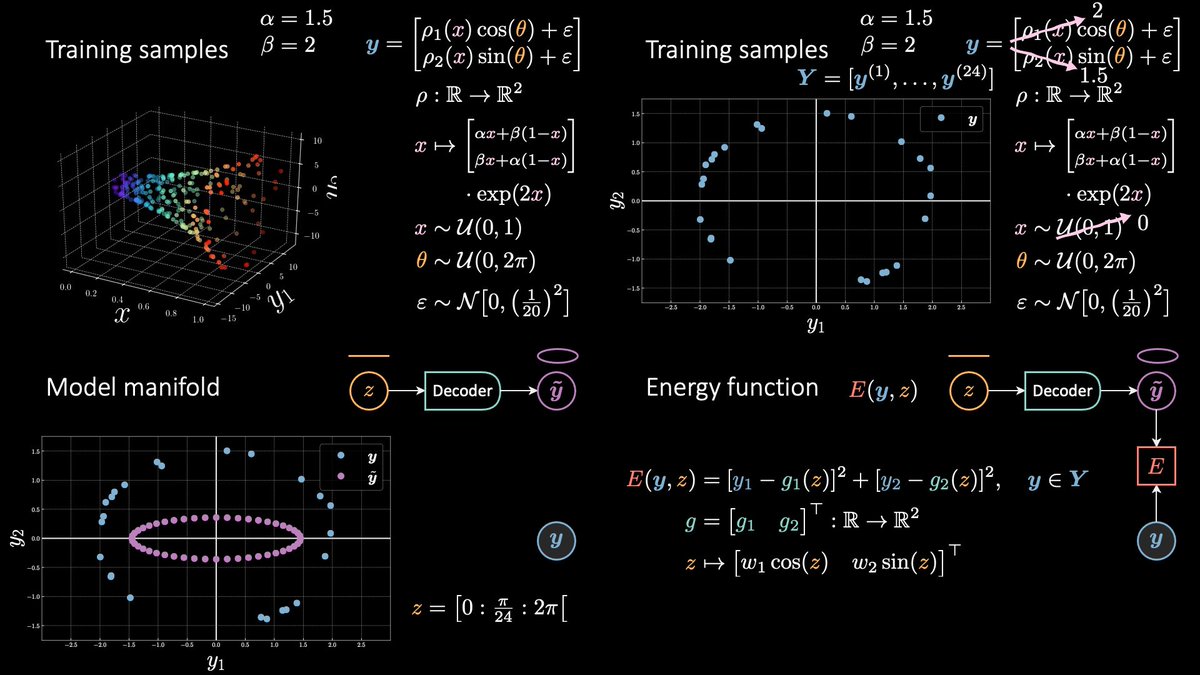
The classical definition of an encoder-decoder architecture is the autoencoder (AE). The (blue / cold / low-energy) target y is auto-encoded. (The AE slides are coming out later today.) 
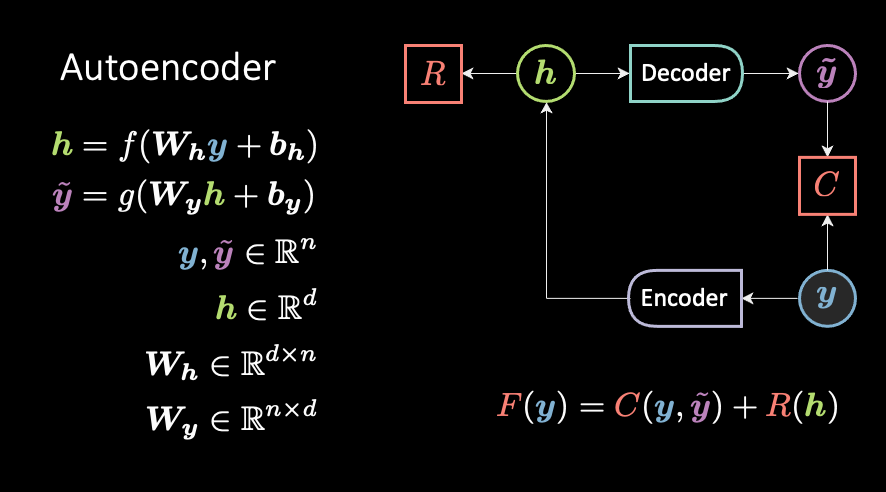
Now, the main difference between an AE and a language-model (LM) is that the input is delayed by one unit. This means that a predictor is necessary to estimate the hidden representation of a *future* symbol.
It's similar to a denoising AE, where there is a temporal corruption.
It's similar to a denoising AE, where there is a temporal corruption.

We also saw how a conditional predictive energy based model includes an additional input x (in pink). The input x can be considered as “context” for the given prediction. 

Now, putting the two things together, we end up with a 2×encoder-predictor-decoder type architecture.
This is what was going on in my mind when I was just trying to explain how the “encoder-decoder transformer architecture” was supposed to work. Well, it didn't make any sense. 🙄
This is what was going on in my mind when I was just trying to explain how the “encoder-decoder transformer architecture” was supposed to work. Well, it didn't make any sense. 🙄

For the part concerning the attention, you can find a summary below.
https://twitter.com/alfcnz/status/1252802274080022528
In addition to which, I've added the explicit distinction between self-attention (thinking about how to make pizza) and cross-attention (calling mom, asking for all her pizza recipes) slide. 

• • •
Missing some Tweet in this thread? You can try to
force a refresh