Thread by @JamesWard73

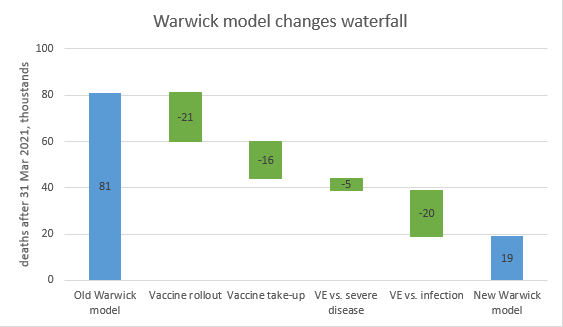
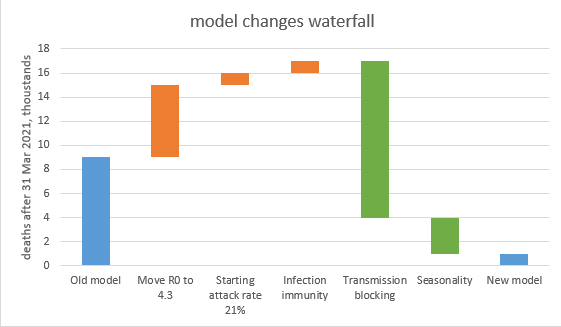
So today’s big covid Twitter debate has been the relative contribution of lockdown (or, more broadly, controls / NPIs) and vaccinations to bringing down case rates. It occurs to me that we already have some numbers – or at least assumptions – that we can look at: 1/4

This chart shows the assumptions in my model for the relative reduction in R from controls, and from immunity. As you’d expect, in January it’s nearly all controls – and by June it’s mostly immunity. The cross-over point is in mid-April – in fact, round about now. 2/4

But of course immunity is a composite of vaccination-acquired immunity, and infection-acquired immunity. So let’s split those out. We can see that infections grow slowly, and have already been overtaken by vaccines. But vaccines don’t overtake controls until early June. 3/4

(note the bump on the blue line in late May is half term, as I assume slightly lower R in school holidays. The control reduction after 21/6 is shown as 10%, but could be higher or lower depending what baseline controls the government retains, and how effective they are.) /end

PS it seems I need to clarify my intent here: by showing these graphs, I'm not expecting to convince anyone who doesn't already believe that controls/lockdown have a big impact on R. I'm just being transparent about the assumptions in my model, which some may find interesting.