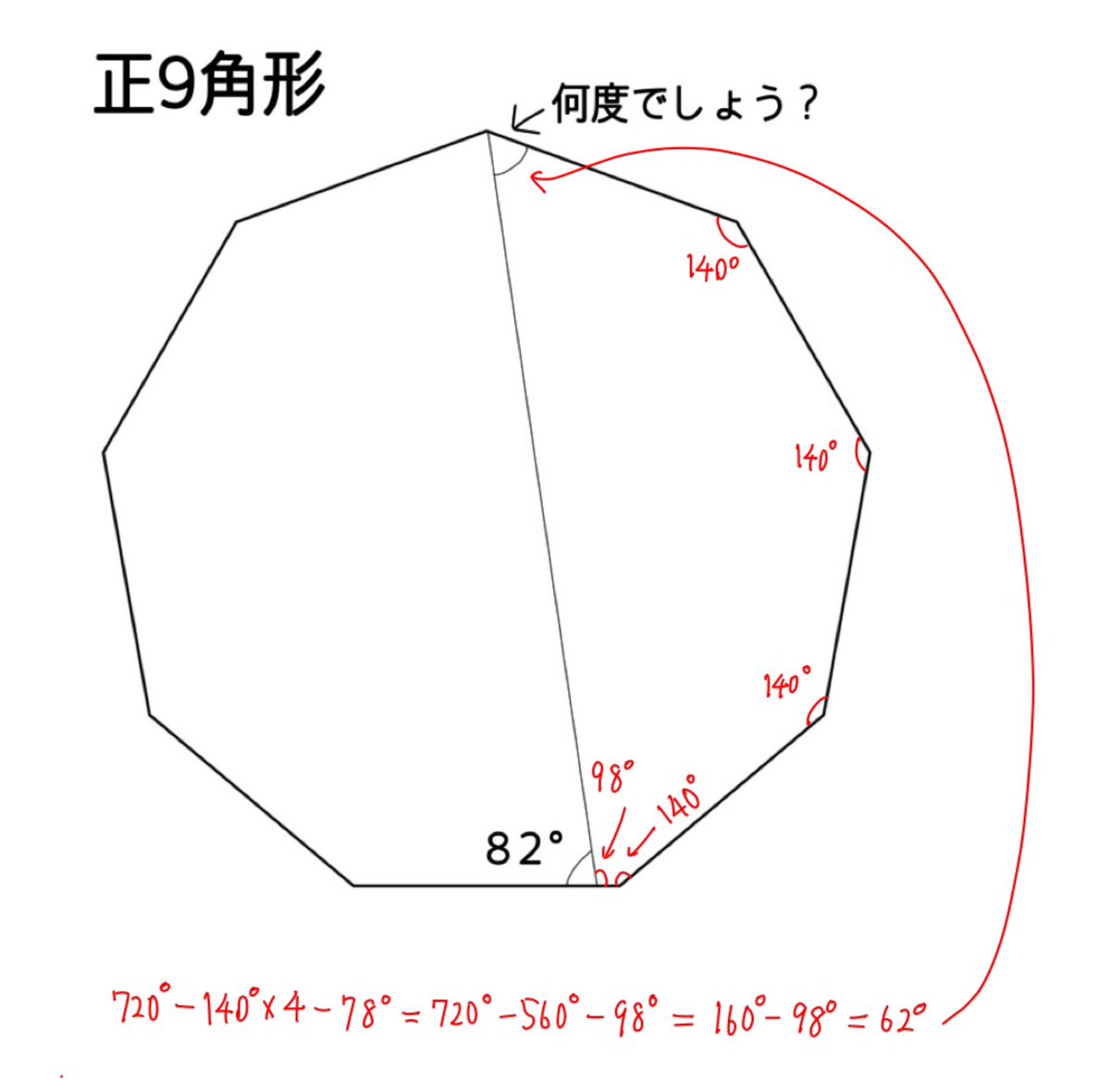
#数楽 子が次の問題を解き始めたので、私が心の中で「正9角形だから各頂点での外角は40度で云々」と考え始めた直後に、「できた!」と言われてくそびっくりした。
10秒で解いた!
解き方が本質を突いていて非常に感心してしまった。
色々な解き方に続く。
10秒で解いた!
解き方が本質を突いていて非常に感心してしまった。
色々な解き方に続く。
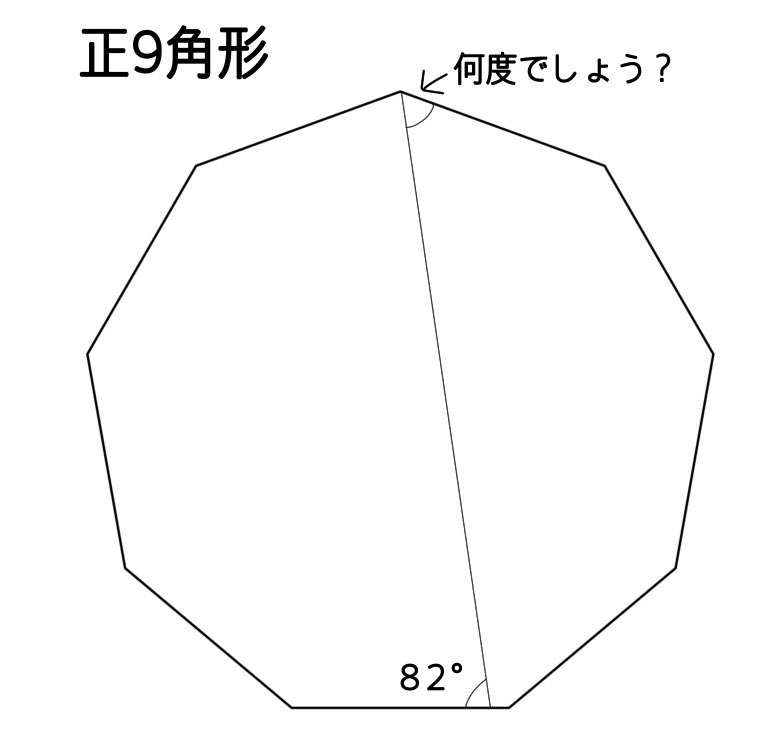
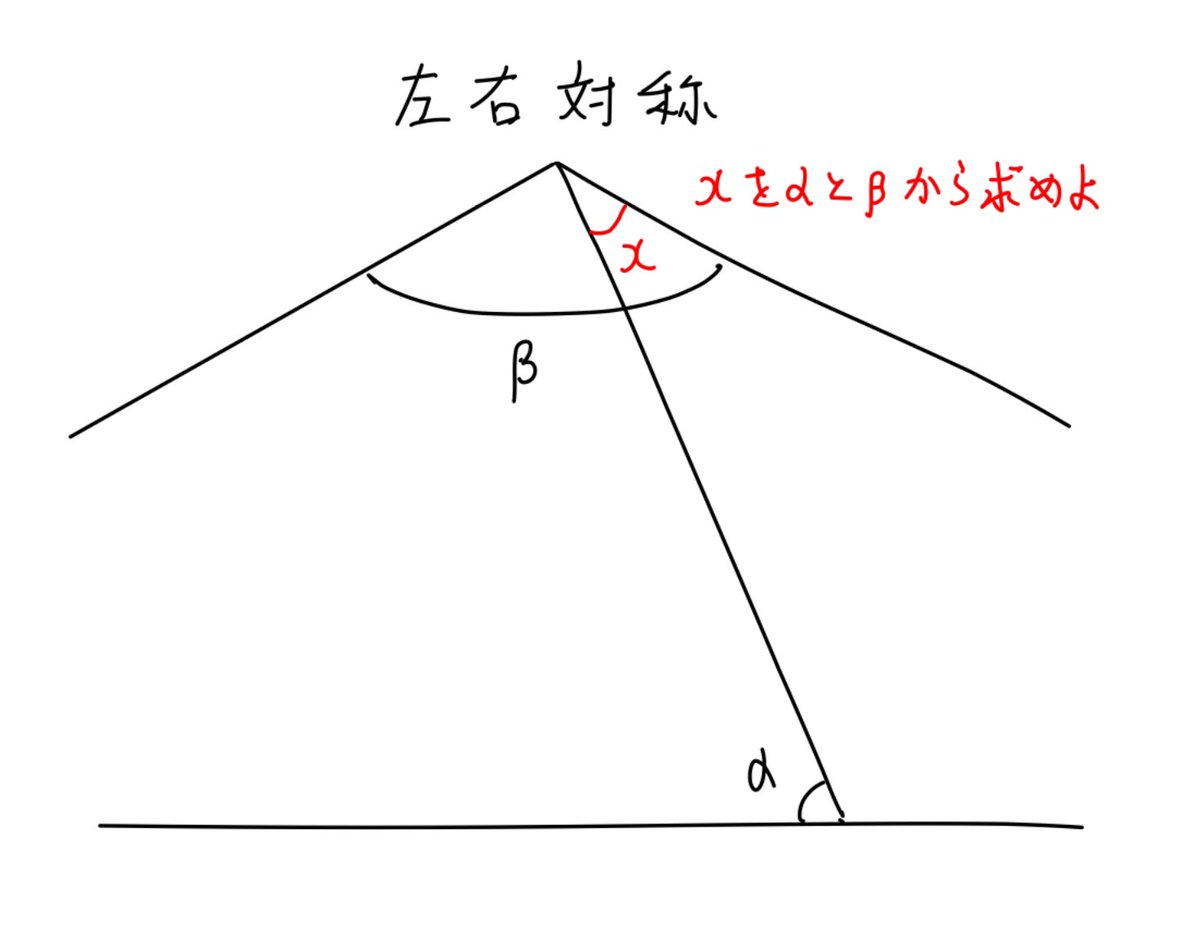
#数楽 無駄な情報を削ぎ落とすと、この問題では「正9角形」という情報は余計で、以下のように見えていれば余計な情報に惑わされずに楽に解ける。
上の問題では正9角形だったので余計な情報に惑わされてもそう悲惨なことにならないが、一般にはそうではない。
というわけで、色々感心してしまった。
上の問題では正9角形だったので余計な情報に惑わされてもそう悲惨なことにならないが、一般にはそうではない。
というわけで、色々感心してしまった。
• • •
Missing some Tweet in this thread? You can try to
force a refresh