Thread by @fgrosshans

Today’s morning session at the @InHenriPoincare is a tutorial “Verification of Quantum computing” by Elham Kashefi

A recent review: arXiv:1706.06984 arxiv.org/abs/1709.06984

#LTQI

Elham Kashefi: Verfication addresses different questions.
1) Test the hardware (tomography like)

2) Test the application: Test is honest behaviour if we use quantum computer for secrecy, test if the answer is correct if we use QC for speed
#LTQI

Elham Kashefi: If a QC solves a classically intractable problem, how can we “verify” the outcome of experiment ?
In complexity ∃MA, Merlin-Arthur: problems who can be verified in BPP when given a proof (aka witness).
But we thing BPQ≠MA.
Even if BQP⊆MA, proof is hard to find

Elham Kashefi: Looking at interacting proofs, IP=QIP: for unlimited prover, a QC doesn’t bring anything to the verifier.
Question: Dose every language ∈BQP admit an IP protocol where the *prover* is restricted to BQP ?

#LTQI

Elham Kashefi: In current verification protocols, either the verifier exchanges qubits with the prover, or the prover has 2 non-communicating but entangled computers

Elham Kashefi:
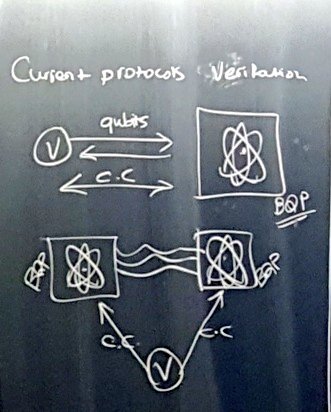
Open question: ∃? a protocol with single BQP prover interacting classically with a BPP verifier?

Actually, the pb of several non-communicating and non-entangled provers is also open. The previous protocol uses entanglement in the honnest case.
#LTQI

Elham Kashef: All these protocol use the technique of blindness (computing on encrypted data)
cf @jfitzsimons’ arXiv:1611/10107 arxiv.org/abs/1611.10107

Idea: delegate computation to remote computer s.t. target comutation is indistinguishable from any other of same length
#LTQI

Elham Kashefi: The client does easy computation (low depth), and the server complex ones.
If the protocol is computationnally secure : (Quantum) Fully Homomorpic Encryption (FHE / QFHE)
If informationally secure: Blindness

#LTQI

Elham Kashefi: For single server verification, several cases:
1) prepare–send client (client : constant size QC)
2) Measuring client
3) Repeated run
#LTQI

Elham Kashefi start to construct a blind protocol using QKD And teleportation. She uses gate teleportation, with a measurement in the XY plane and a random phase θ, compensated in the measurement
#LTQI

Elham Kashefi: schematics of the previous tweet #LTQI

Elham Kashefi then add a random phase rπ (r is 0 or 1) to the measurement and obtains her scheme, with the client preparing the state P(θ)Z^i|+> and making the final bitflip X (taking r into account).
The server does the rest (CZ, measurement)
#LTQI

Elham Kashefi:
rπ prevents a leak from the output.
α defines the computation, but the server only sees δ=α+θ+rπ, which is uniform.
Combining this little gadget with a bunch of control Zs to create a universal graph state allows to make universal blind QC (UBQC)
#LTQI

Elham Kashefi:
For UBQC, Alice should translate the cricuit C into a graph MPQC (G,α). Since the graph could leak some information on the computation, one should use a (potentially wasteful) graph pattern
#LTQI

Elham Kashefi:
The secret is now the set of α .
Alice send the states |+_θ⟩= P(θ)Zⁱ|+⟩ to Bob/Server
Bob creates graph state |G⟩
For each i
Alice sends δ=α+θ+rπ⟩
Bob makes the measurement and obtains b_i and sends it to ALice
Alice computes b⊕r=s, the result

#LTQI

After the coffee break, Elham Kashefi defines ε-verifiability and δ-correctness:
Verification is a protocol where probabilitiy(witness accepted and outcome is bad)≤ε.
#LTQI

Elham Kashefi then formalizes the above definition:
The verifie state is |ψ⟩|flag⟩, where flag∈{acc,rej}. Initally flag=acc
There’s and encoding channel Enc^s depending on verifier channel, depending of private random variable s of verifier
#LTQI

Elham Kashefi:
P_honnest applies a CPTP
P_incorrect^s=(I-|ψout^s⟩⟨ψout^s|)⊗|acc^s⟩⟨acc^s|
ψout^s⟩⟨ψout^s|=Tr_flag( Phonnest(Enc^s|ψ⟩⟨ψ|)⊗|acc⟩⟨acc|))
|acc^s⟩⟨acc^s|=Tr_input(⋯)
ε-verifiable⇔ Tr(∑_s p(s) Pincorrect^s P(Enc^s(|ψ⟩⟨ψ|)⊗|acc⟩⟨acc|)))≤ε
#LTQI

Elham Kashefi:
A protocol is δ-correct iff
Tr(∑_s p(s) Pincorrect^s Phonnest(Enc^s(|ψ⟩⟨ψ|)⊗|acc⟩⟨acc|)))≥δ
#L

Elham Kashefi:
The challenge in finding an ε-verifiable verifiable: The P in the middle of the definition is an arbitrary CPTP map, preformed by a dishonnest prover

#LTQI

Elham Kashefi:
A common tool is Clifford Pauli twirling, where C used for encryption/decryption:
∑_C C⁺P₁CρC⁺P₂C =0
with P₁≠P₂ Paulis
sum over either C∈Clifford or C∈Paulis
#LTQI

Elham Kashefi, For any encoding, we have
ℰ(ρ)=∑ Ki ρ Ki⁺ with ∑Ki Ki⁺ =1
Ki = ∑αj Pj
ℰ(ρ)=∑_ijk α_ij α_ik^* Pi ρ Pj⁺
∃ annoying croos terms above: solution=use twirling theorem above
#LTQI

Elham Kashefi:
The encoding Enc introduce a random Clifford/Pauli
⇒
ℰ(ρ)=∑a_ij^* Pi ρ Pi

#LTQI

Elham Kashefi:
To make a concrete UBQC protocol, one also need to define a flag:
create a trap, a |+_θ⟩ at random position, surounded with dummy qubits (|0⟩,|1⟩).
The result of the measurement is deterministically r
#LTQI

Elham Kashefi:
The UBQC protocol is then modified into VUBQC.
I. The graph G has to admit T trap-qubits and D dummy-qubits. E.g. consider a cylindrical cluster state, cut by a (random) line of traps into flat cluster states. (∃more efficient graphs)
#LTQI

Elham Kashefi:
Then the qubits are in 3 sets Q (computation) T (trap) D (dummy).
Alice behaves the differently for the different qubits type, as expected.
Then finally, accepts the computation iff the trap qubits gave the expected answer.
#LTQI

Elham Kashefi:
There is a link between ε and he number of traps. Let’s compute ε for one trap. We find 1–1/N, the probability to hit the trap.
With a constant fraction of traps, we have ε=8/9.

For an exponential bound at a linear cost, repeat d times, and ε=(8/9)^d

#LTQI

Elham Kashefi:
This is a universal protocol. If one is only interested to a specific family (IQP, Clean-qubit, etc.) it can be simplified.
It seems to always be possible to adpat this technique, except for CV (no twirling)
#LTQI