Thread by @AndrewCAhn2

My goal for these #Tweetorials is to empower you to apply engineering/physics concepts to clinical care. To do this, we will do "deep-dives", going deeper than typical physiology courses and applying to real clinical cases. In this thread, we go deeper into Laplace's Law.
1/20

Last week, I had a patient with hydronephrosis. Looking at CT scans, have you noticed that the renal pelvis usually dilates out of proportion to the ureter? To me, the ureter is often tough to trace 2/2 smaller diameters. Can Laplace explain this?

2/

Just to review: Laplace's Law describes the force relationship between the surface (Tension) and interior space (Pressure). This relationship is influenced by size (i.e., Radius) and shape (cylinder vs. sphere). See the formula here:

3/

Note: for a given T (tension) and R (radius), the sphere generates 2X as much P (pressure) as the cylinder. You can see that in the balloon where the tension on the rounded portion is less than cylindrical part, despite the same internal pressures. Q: Why is that?

4/

As mentioned previously, Laplace applies to systems in equilibrium. Several ways to interpret this.

(1) ENERGY: amount of work (change in energy) needed to expand the surface is balanced by the amount of work done by interior air/liquid.

5/20

Imagine an inflated balloon at equilibrium. If balloon is to expand, work needed to expand the volume exceeds work relieved from the surface's contracting forces. Conversely, for balloon to contract, the contracting work by surface exceeds the relief of work by the volume.

Another way to interpret.

(2) FORCE: At equilibrium, the force performed on the surface (by the interior material) is balanced by force performed on the interior (by the surface). One can derive the same Laplace's Law equations using this perspective.

7/

Ans: Sphere is able to generate more pressure because its surface tension contributes to radial forces (to counter Pressure) from all directions, whereas for the cylinder, only surface tension along the circumferential direction (not longitudinal) contributes to radial forces

So for a given T (surface tension), how can one can ensure higher P (pressures). Objects should have:

Answer is D.

Now consider a blind viscus (a cylindrical portion connected to spherical one):

What is the expected ratio for the two Radii assuming identical tension (T) & thickness (w)?

10/20

What does it mean when the average radius of ureter (adult) is ~ 1.5-2 mm while renal pelvis ~ 5-6 mm?
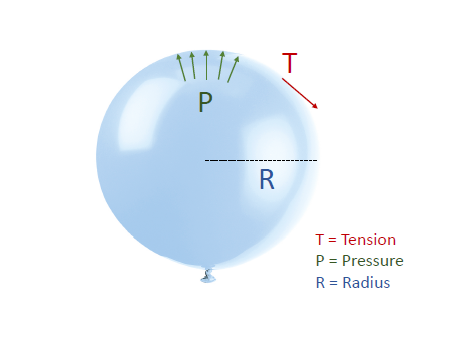
Since renal pelvis > 2x ureter radius, it indicates that tension/thickness of ureter wall is greater than that of renal pelvis! (As expected d/t muscle in the ureter wall)

As pointed out by few astute readers in the last thread, the assumption that T (tension) remains constant (as in alveoli or compressive stockings examples) should not hold true. They are absolutely correct! As R increases, T (and thus P) should increase too.

12/20

But Tension is complicated.

First, there can be viscoelastic properties in biological tissues (non-linear/hysteresis).

Second, T does not always increase linearly with R. E.g.: Inflating a balloon. Above a certain Volume, Pressure decreases (seen in 2-balloons). Why?

I really struggled with this for a while. If R is increased, shouldn't T increase (and thus P) as well? There were so many conflicting explanations floating out in the internet...

14/20

After some calculations, I found out - it's all about THICKNESS!

As the balloon inflates, its walls thin out and T decreases. In fact, P is maximum at the "limit-point instability". Above this threshold, the balloon can expand rapidly until risk of rupture.

This thickness factor explains why it is harder to blow a Cylindrical balloon above a certain volume. (Recall: Laplace predicts that Spherical balloon requires higher pressures to inflate). The explanation lies in its geometry (see slides).

16/20

So, when considering Laplace law, consider not only the shape, but also the decreasing thickness.

Based on calculations, this occurs at 1.5x non-distending Radius for Sphere and 2.0x non-distending Radius for Cylinder.

So back to hydronephrosis. How would these factors predict how renal pelvis and ureter dilate with hydronephrosis? Using average adult dimensions, ureter wall elasticity, the model shows the following.

18/20

Ureters will not dilate significantly unless surpassing the limit-point instability, well-after the renal pelvis has already dilated significantly. Explains why radiologists grade hydronephrosis according to calyceal blunting, renal pelvis size (not ureter diameter).

19/20

Summary:

* Laplace is function of T, R, P, thickness, and shape
* For given surface tension, spheres generate more pressure than cylinders
* Tension properties are complex and depend on each use case
* Thickness is an important factor for larger radii/diameters