==================
A microtweetorial because I have been watching @anupampom and @JohnTuckerPhD chase each other like this for the last hour, which is distracting me from doing work.
Answer this and save them from circular argument.
#foamed #meded
I am really, really pleased with the result and the fact that I have the patent on this magical stuff.
A. 3% of pts had reduced atherosclerosis?
B. 97% of pts had reduced atherosclerosis?
C. If a drug is ineffective, 3% chance that it produces an effect this extreme.
D. 3% probability that THIS drug is ineffective, i.e. that these results occurred by chance
At 30 votes, here is the distribution.
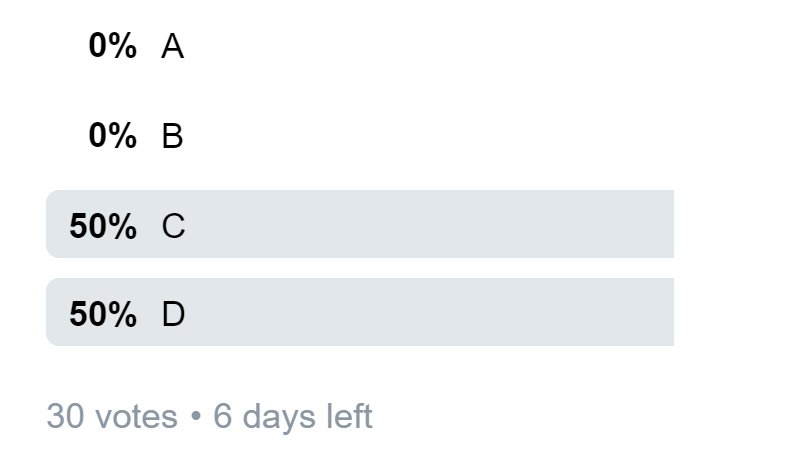
People who've answered already, don't give the game away please. Let me take everyone through this as it is difficult but fundamental to interpreting clinical trial data, or indeed any hypothesis testing (p values).
They are organic, renewable and biodegradable. In short, they are lawnmower cuttings diluted in water.
F.A.K.E. has run a series of trials, FAKE-1, FAKE-2 etc.
However, FAKE has deep pockets and ran many trials.
In fact, 200 of them.
How many of them would be expected to have p<0.05?
===
When you run a trial you will find that FAKE-1 recipients do slightly better or slightly worse than Controls, through chance.
Individual patients do differently.
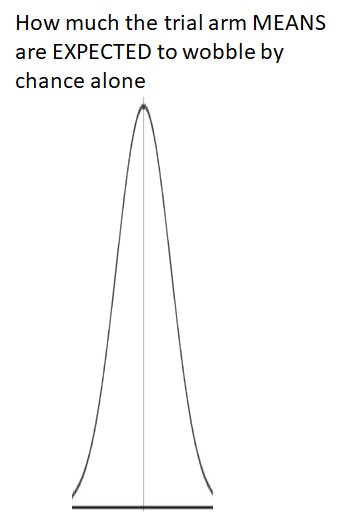
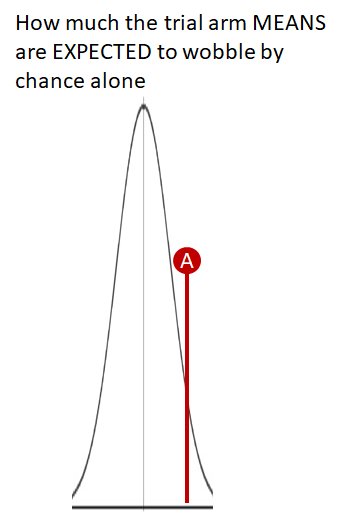
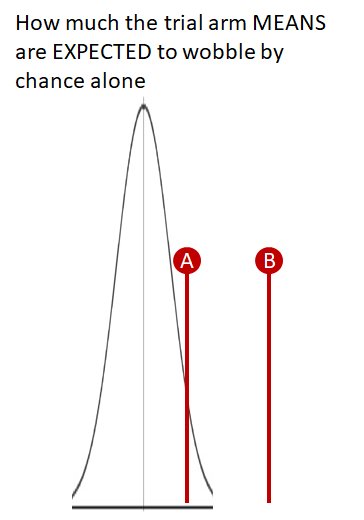
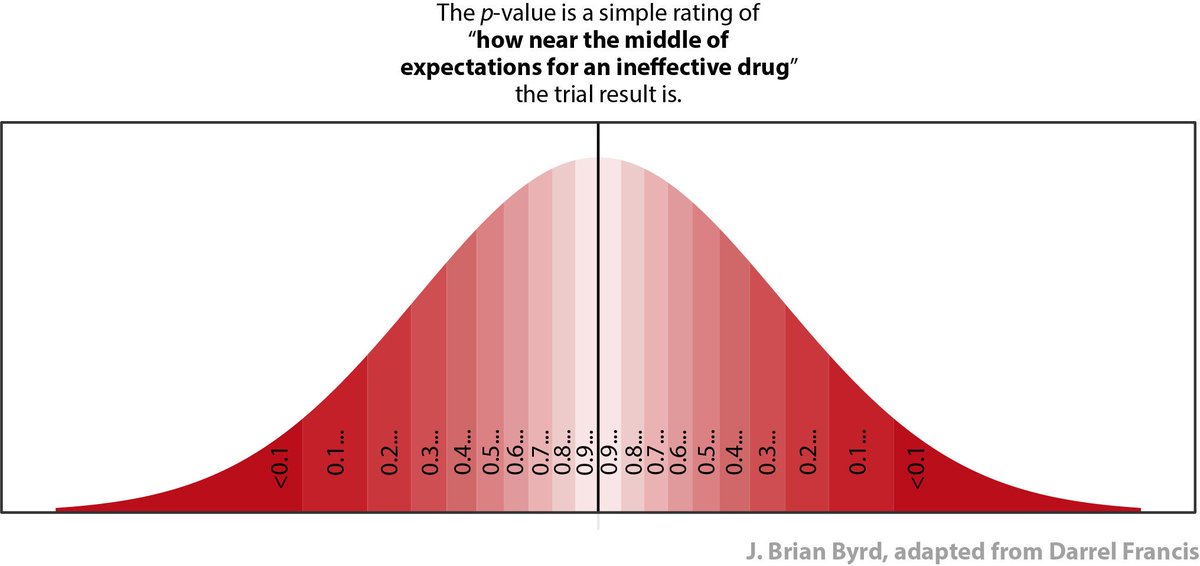
On this scale, p=1.00 means "absolutely exactly average of expectations, for a drug that does not work."
😋
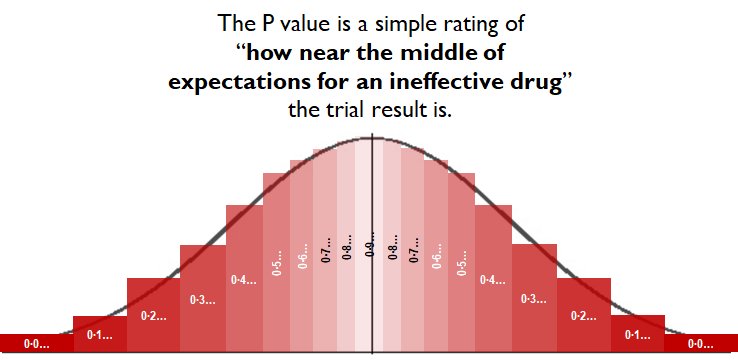
The statistics calculate where the trial result lies on that spectrum.
Near the middle, and the stats return "P=0.9..something"
"Wow! A truly useless drug would be unlikely to be this lucky or unlucky."
------------------------
I sketched the above in PPT between caths just now. It's not very good.
I would be grateful if someone can draw it correctly, in R or Excel or something.
Don't use rectangles, use trapezia, so it doesn't look so zany at the top.
NORMINV(0.025, 0, 1)
NORMINV(0.075, 0, 1)
etc, to
NORMINV(0.975, 0, 1)
The y-coordinate for each x should be
NORMDIST (x, 0, 1, FALSE)
Tweet or DM it to me, and I will credit when using in future.
====================
P values are automatically generated by statistics, in a way that INEFFECTIVE interventions produce P values UNIFORMLY distributed between 0 and 1.
0.32 is just as likely as 0.78 and 0.02.
So, IF THE DRUG IS INEFFECTIVE, what is the probability of getting a P value:
BETWEEN 0.2500 and 0.3500?
between 0.000 and 0.0499...
=================
In amongst those trials (5, 10, 15, or 20, however many you said above) where the P value is <0.05,
In WHAT PROPORTION OF _THOSE_ TRIALS is the drug actually genuinely any good?
(Remember it is just lawnmower shreddings and water.)
P is the probability that IF YOU START WITH A USELESS DRUG, you get a result like this.
It is NOT the probability that IF YOU GET A RESULT LIKE THIS, the drug is useless.

Evidence of this lack of awareness is the current state of the vote on the first question:
At 300 votes:
rss.onlinelibrary.wiley.com/doi/epdf/10.11…
They may be a WOMAN (or not)
They may be PREGNANT (or not)
Q1
*If* they are a woman, what is the probability they are pregnant?
*if* they are PREGNANT, what is the probability they are a woman?
So much so that mathematicians, who hate getting confused, have a special notation for it.
They write it
P (Thing that MIGHT be true | Thing that is ALREADY KNOWN TO BE TRUE)
You can read this as:
"What is the probability of a person being a woman, GIVEN THAT you already know they are pregnant?"
You can read this as:
"What is the probability of a person being pregnant, GIVEN THAT you already know they are a woman?"
The P value of a trial is:
P (A result as exciting as this or more so | Drug is, in fact, CRAP)
It is not the probability that anyone actually wants. It all backwards.
We can't even convert it into the probability we want.

However 5% of the time, the result will have P<0.05.
If you try out ONLY RUBBISH DRUGS, what proportion of the P<0.05 results you get will be genuinely beneficial drugs?
- mainly GOOD drugs
- mainly RUBBISH drugs
- 50:50 mix
- some other mix
We have absolutely no idea.
So there is NO POINT expecting our standard stats to tell us P(Drug is rubbish | Got the result we got).
It can't.
There is another approach to stats called "Bayesian", which (if we could do it perfectly) would give us the probability we actually wanted, namely "how likely is this drug to be rubbish?"
But I also understand the principles of doing a Heart-Lung transplant.
Doesn't mean I would actually try to do either, myself!
This tweetorial only covers Frequentist, which is the great majority of published medical statistics.
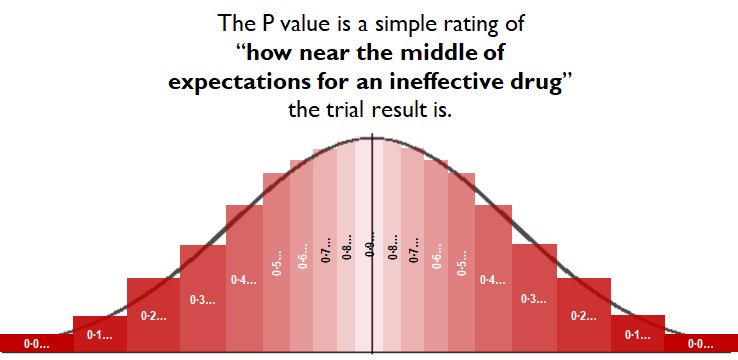
What does p=0.03 mean?
A. 3% of pts had reduced athero
B. 97% of pts had reduced athero
C. If a drug is ineffective, 3% chance that it produces an effect this extreme or more
D. 3% probability that THIS drug is ineffective, i.e. that these results are chance
P values tell you the following.
IF THIS DRUG IS INEFFECTIVE, the chance of a result like this (or more extreme) is 0.###.
Can we try again please?
Fingers crossed...
Third time lucky...
Got p=0.03.
What does this mean?
C. An INEFFECTIVE drug would be expected to produce a result as extreme as this (or more so) in only 3% of trials.
D. There is 3% probability that THIS drug is ineffective.
Remember that a the statistics generate your P value as a handy rating of how RARELY a trial of an INEFFECTIVE drug would have a result as dramatic as this (or more so).
Remember the Uncle Darrel red-o-gram?
Remember when we first did this, the majority were wrong. So this is a big improvement in the hardest thing to understand in the whole of medical stats.
Got p=0.03.
What does this mean?
C. An INEFFECTIVE drug would be expected to produce a result as extreme as this (or more so) in only 3% of trials.
D. There is 3% probability that THIS drug is ineffective.
It was because of inertia. It is very difficult to change the velocity (speed and direction) of a very heavy object.
A huge amount of impulse is needed.

It is ONLY showing us what an imaginary INEFFECTIVE drug would be expected to do. How rarely a trial result of an INEFFECTIVE drug would be as extreme as this or more so.
And more importantly how SLOWLY we shifted the Titanic of Twitteropinion as I repeated the same question through this tweetorial.
Develop an efficient and memorable way to explain to medical colleagues in general what a P value actually means.
Test it like in this tweetorial, but also by retest at a later date.
But you will be contributing an enormous amount to medical care worldwide and everyone will be genuinely interested in your PhD.

Zeroth Law of Statistics,
J Articles Rej By J Quantum Theor.