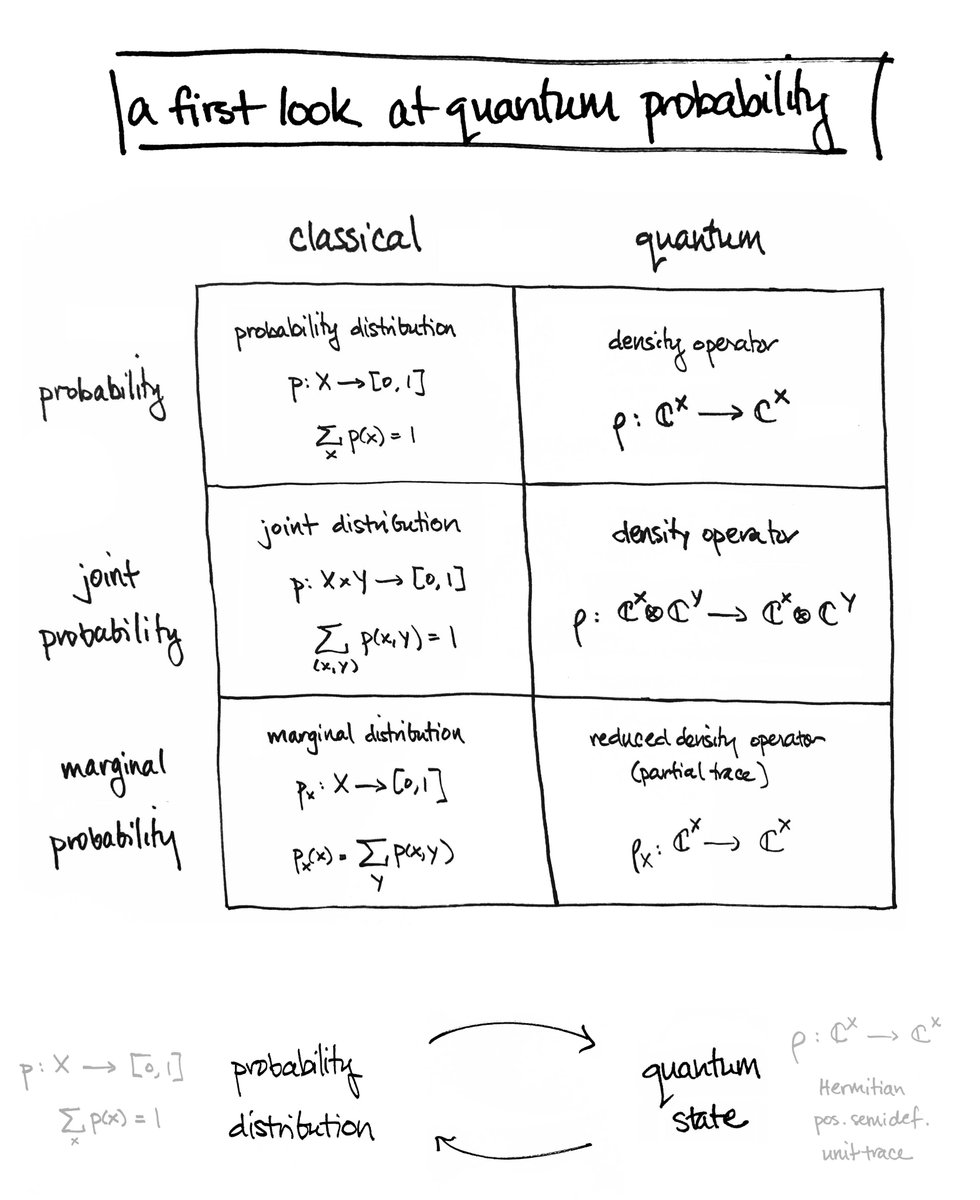
But what do these words mean??
I’ll explain...
The answer is yes! You can do it by a construction in linear algebra called the particle trace.

Get real-time email alerts when new unrolls are available from this author!
Twitter may remove this content at anytime, convert it as a PDF, save and print for later use!

1) Follow Thread Reader App on Twitter so you can easily mention us!
2) Go to a Twitter thread (series of Tweets by the same owner) and mention us with a keyword "unroll"
@threadreaderapp unroll
You can practice here first or read more on our help page!