Thread by @AlexandreIMPA

Olá pessoal, a convite do @rationalexpec (desde já agradeço pelo convite), farei uma thread sobre testes de hipóteses, e p-valor, que espero que seja acessível a todos que tenham um background básico de probabilidade (essencialmente, que saiba o que é uma variável aleatória).

@rationalexpec Uma hipótese estatística é uma hipótese que podemos testar a partir de um conjunto de dados, onde cada observação pode ser vista como uma variável aleatória em algum espaço de probabilidade.
A hipótese só pode possuir dois valores: Verdadeiro ou Falso (sem paradoxos, galera! 😂)

@rationalexpec A partir da hipótese estatística construímos duas hipóteses: nula e alternativa.
Hipótese nula (denotada H_0): é uma hipótese que, normalmente, vai contra o que queremos provar;
Hipótese alternativa (denotada H_1): uma hipótese de acordo com o que queremos provar.

@rationalexpec Desta forma, testa-se a hipótese nula contra a hipótese alternativa.
Assim, só rejeitamos a hipótese nula se tivermos evidência forte o suficiente contra ela (um análogo de evidência de culpa “beyond any reasonable doubt” dos julgamentos, para condenar um suspeito).

@rationalexpec Quando testamos hipóteses, podemos cometer dois tipos de erros:
Erro tipo I: Rejeitar a hipótese nula dado que ela é verdadeira;
Erro tipo II: Não rejeitar a hipóese nula dados que ela é falsa.

Fato triste: Matematicamente, não conseguimos controlar os dois erros ao mesmo tempo.

@rationalexpec Matematicamente é possível:
1: Controlar o erro tipo I;
2: Controlar o erro tipo II;
3: Controlar combinações lineares entre os erros tipo I e tipo II.

Desta forma, o que costuma-se fazer normalmente?
O exemplo abaixo nos ajuda a ilustrar o que costuma ser feito.

@rationalexpec Exemplo ilustrativo (não estatístico mas que ajuda a esclarecer os conceitos): Considere um julgamento de um suspeito, onde a promotoria quer provar a culpabilidade dele. Assim a promotoria tem a hipótese “O suspeito é culpado” e quer testá-la.

@rationalexpec Neste caso, a promotoria vai trabalhar com as seguintes hipóteses:
H_0: “o suspeito é inocente” (é a hipótese contrária à tese dela e que precisa de evidência forte para ser rejeitada);
H_1: “o suspeito é culpado”.

Erro Tipo I: Condenar inocente;
Erro Tipo II: Soltar culpado.

@rationalexpec O que é considerado mais grave?
É um consenso que é mais grave condenar um inocente e assim, neste caso, haveria uma preferência por controlar o erro tipo I.

De fato, é isso que é feito nas análises estatística: controla-se o erro tipo I.

Mas… O quer dizer controlar o erro?

@rationalexpec Controlar o erro tipo I, é controlar a probabilidade do erro tipo I ocorrer. Ou seja, é possível construir testes de tal forma que sabe-se que a probabilidade de ocorrer um erro tipo I é x%, ou seja, pode-se escolher 1%, 5%, 10%, 20%, etc. O nível padrão é 5%.

@rationalexpec Agora que já entendemos os conceitos básicos relacionados às hipóteses estatísticas, vamos entender como os testes de hipóteses são construídos.
A primeira definição que precisamos é de “estatística” (não a ciência, mas sim uma definição matemática).

@rationalexpec De maneira informal, dada uma amostra (isto é, uma coleção de variáveis aleatórias) X_1, …, X_n, uma _estatística_ é uma função dessa amostra. Existem mais tecnicalidades, mas podemos ignorá-las nessa exposição.

Exemplo de estatística: média amostral (X_1 + … X_n)/n

@rationalexpec Assim,para realizarmos testes de hipóteses em uma amostra, queremos construir estatísticas que se comportem de um jeito de a hipótese nula for verdadeira e de outro jeito se a hipótese nula for falsa.

Matematicamente,queremos que a distribuição da estatística mude com a hipótese

@rationalexpec Isto é, se a hipótese nula for verdadeira, a estatística tem uma distribuição A, e se ela for falsa, a distribuição da estatística é B, e temos que A é diferente de B.

Neste caso, a estatística é chamada de “estatística do teste”.

@rationalexpec Importante: A distribuição da estatística do teste, sob a hipótese nula, não pode depender de nenhum parâmetro desconhecido, porém a estatística em si pode depender de parâmetros desconhecidos.
Um exemplo clássico é a estatística t para uma amostra normal iid.

@rationalexpec A estatística t depende do parâmetro desconhecido mu, porém sob a hipótese nula H_0: mu = mu_0, a distribuição da estatística não depende de nenhum parâmetro desconhecido.
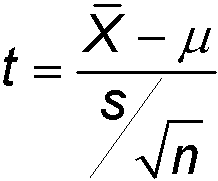
É diferente do estimador, que não pode, de forma alguma, depender de parâmetros desconhecidos.

@rationalexpec Se tivermos uma estatística de teste, como fazer para usá-la para testar a hipótese nula?

Como queremos controlar o erro tipo I (onde supomos que a hipótese nula é verdadeira), supomos que a hipótese nula é verdadeira, e obtemos a distribuição da estatística do teste em questão.

@rationalexpec Obs:Com frequência não consegue-se obter a distribuição exata da estatística do teste sob a hipótese nula, porém,é comum conseguirmos obter a distribuição assintótica sob a hipótese nula.
Assintótica aqui costuma significar o caso limite quando o tamanho amostral tende a infinito

@rationalexpec Neste caso assintótico onde o tamanho amostral foi pra infinito, o resultado do teste só terá validade estatística se o tamanho amostral for muito grande. Em geral, os tamanhos sugeridos para termos confiabilidade são obtidos via simulações.
Mas temos outros casos assintóticos…

@rationalexpec Podemos ter o chamado “small dispersion asymptotics”, quando a variância tende a zero (não muito comum), e também o caso de uma partição sendo refinada num intervalo (comum em análise de dados de alta frequência), entre outros.

@rationalexpec Voltando ao teste estatístico, vamos então supor que conhecemos a distribuição (exata ou assintótica) da estatística do teste sob a hipótese nula.

Como já vimos que o padrão é “controlar” o erro tipo I, vamos controlar a probabilidade do teste “errar” sob a hipótese nula.

@rationalexpec Como temos a distribuição (exata ou assintótica) sob a hipótese nula, o que fazemos é: escolhemos um nível de significância alpha (ou seja, probabilidade de cometer erro tipo I) e obtemos uma região (que denotaremos por C) de valores que a estatística do teste pode assumir

@rationalexpec De tal forma que:
P_0(Estatística do teste PERTENCER à região C) = 1 – alpha,
onde P_0 é a medida de probabilidade supondo H_0 verdadeira, tal que conhecemos a distribuição (exata ou assintótica) da estatística do teste.

C é chamada de “região crítica” e depende de alpha.

@rationalexpec Assim, é possível que H_0 ser verdadeiro a estatística cair fora de C. Mas isso ocorre com probabilidade alpha (que deve ser pequeno)
Normalmente trabalha-se com o nível de significância alpha = 5%, é chamado de nível de significância padrão ou usual.

@rationalexpec Não tem nada de mágico nesse número e sua escolha é simplesmente um costume. Em alguns casos escolhe-se 1% ou 10%.

Fim da parte 1 da thread!

Já ficou longa. Fim de semana que vem (se houver interesse) teremos a Parte 2!

@rationalexpec Na parte 2 veremos: Testes paramétricos e não-paramétricos e exemplos; Poder do teste; Hipóteses simples e compostas; Lema de Neyman-Pearson; Definição de p-valor; Erros comuns com o uso do p-valor.

@rationalexpec Além disso, na parte 2, veremos uma treta que rolou entre estatísticos de altíssimo calibre sobre qual seria a forma correta de modelar o testes estatísticos. Sugestão do @agpatriota

@rationalexpec @agpatriota Aproveito para agradecer ao @agpatriota e ao @rationalexpec pelas críticas e sugestões.

@rationalexpec @agpatriota Parte 3: Tópicos adicionais (pode sofrer alterações):
Importância de um planejamento de experimentos adequado; Importância das suposições; Testes sequenciais (erros comuns ao fazer), Consistência lógica (ou não!).