Thread by @SchreiberUrs

**Cohomotopy**
ncatlab.org/nlab/show/coho…

=================
The grand unified theory
of differential topology
=================

From spheres to M-theory.
A leisurely thread.

-------------------------------
scroll down for the latest

**Ordinary cohomology**

The ordinary cohomology groups

H*(X,Z)

ncatlab.org/nlab/show/ordi…
satisfy a list of nice properties
called the *Eilenberg-Streenrod axioms*
ncatlab.org/nlab/show/gene…

**Generalized abelian cohomology**

Dropping just one of the ES-axioms
(the "dimension axiom")
yields a larger class of "generalized" cohomology theories
ncatlab.org/nlab/show/gene…

E*(X)

The famous example is
complex topological K-theory

KU*(X)

ncatlab.org/nlab/show/topo…

The **Brown representability theorem**
ncatlab.org/nlab/show/Brow…
states that:

Every such generalized cohomology theory E
has a *classifying space* E_n
for each degree n
such that the n-th cohomology group
is equivalently
the homotopy classes of maps
into the classifying space:

**Examples of abelian classifying spaces**
include:

For ordinary cohomology
ncatlab.org/nlab/show/ordi…
the Eilenberg-MacLane spaces K(n,Z)
ncatlab.org/nlab/show/Eile…

For complex topological K-theory
ncatlab.org/nlab/show/topo…
the stable unitary group U and its BU
ncatlab.org/nlab/show/stab…

**Spectra of classifying spaces**

The Eilenberg-Steenrod axioms demand
that the classifying spaces E_n
of a generalized cohomology theory E
are loop spaces of each other

E_n = Omega E_n+1

making the sequence what is called a "spectrum"
ncatlab.org/nlab/show/Intr…

The **abelian nature of ES-generalized cohomology**

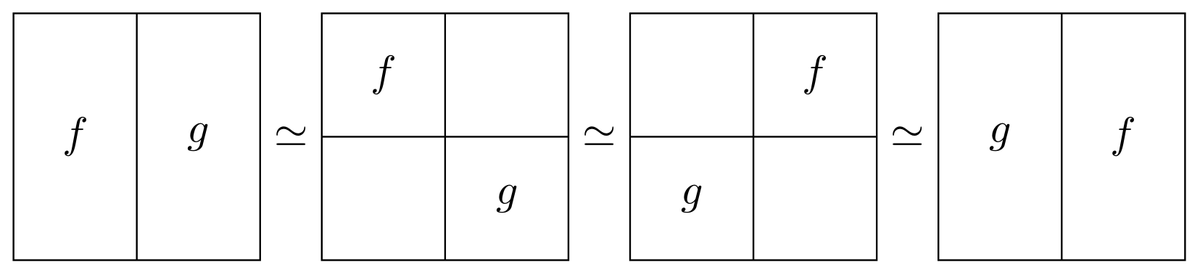
thus arises because multiple-dimensional loops
may be homotoped around
and hence commuted with each other.

This is the Eckmann-Hilton argument:
ncatlab.org/nlab/show/Eckm…

**But not all cohomology theories are abelian!**

For G a non-abelian Lie group
the *first non-abelian cohomology*
H^1(X,G)
is defined on a manifold
as the Cech cohomology
ncatlab.org/nlab/show/%C4%…
of sheaf of G-valued functions
Gives G-principal bundles:
ncatlab.org/nlab/show/prin…

Now, also
**first non-abelian cohomology has a classifying space**
namely *the* classifying space -- BG
ncatlab.org/nlab/show/clas…

This means there is a "Brown representability"
also for first non-abelian cohomology:
It's equivalently
homotopy classes of maps
into BG:

Thus there is an evident
joint generalization of
a) generalized but abelian cohomology
b) degree-1 non-abelian cohomology
namely:

**Non-abelian generalized cohomology**
ncatlab.org/schreiber/show…
for any coefficient space A
is defined to assign the homotopy-classes of maps into A:

The primordial example
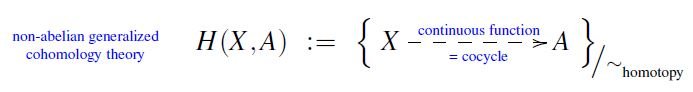
of a non-abelian generalized cohomology theory
is:

**Cohomotopy cohomology theory**
ncatlab.org/nlab/show/coho…

defined to have as classifying spaces
the most basic of spaces
ncatlab.org/nlab/show/CW+c…
namely the n-spheres:
ncatlab.org/nlab/show/sphe…

**Cohomotopy as grand unified differential topology**

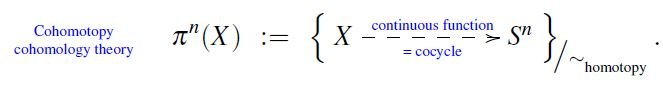
A whole range of classical theorems
in differential topology
ncatlab.org/nlab/show/diff…
all revolve around characterizations of Cohomotopy
ncatlab.org/nlab/show/coho…
even if this is not often fully brought out in the terminology:

On domain spaces which are spheres,
**Cohomotopy groups reduce to
homotopy groups of spheres**
ncatlab.org/nlab/show/homo…
-- the vanishing point of algebraic topology,
the "Music of the Spheres"
ncatlab.org/nlab/show/Musi…

The notable example for the following purpose
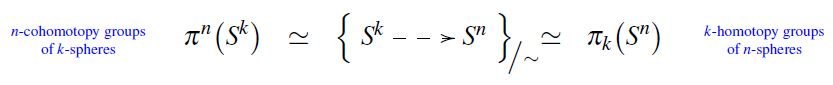
is the
**quaternionic Hopf fibration**
ncatlab.org/nlab/show/quat…
which is a generator of the non-torsion subgroup
in the 4-Cohomotopy of the 7-sphere.

As shown on the right...

...as shown again on the right,
there is an
abelian approximation to non-abelian Cohomotopy theory
called **stable Cohomotopy theory**
ncatlab.org/nlab/show/stab…
whose spectrum of classifying spaces is
the **sphere spectrum**
ncatlab.org/nlab/show/sphe…

In this abelian approximation...

Non-abelian 4-Cohomotopy
witnesses
via the quaternion Hopf fib ncatlab.org/nlab/show/quat…
integer cohomology groups
not only in degree 4,
but also in degree 7
–
but when seen in the abelian/stable approximation
this “extra degree” fades away
and leaves only a torsion shadow behind.

.
.
Chapter I

====================
Twisted Cohomotopy
ncatlab.org/nlab/show/twis…
====================
.
.

.
.
.

**Twisted non-abelian generalized cohomology**
is easy to understand from the perspective
of homotopy theory of classifying spaces:

Instead of mapping into a fixed classifying space,
a twisted cocycle maps into a varying classifying space
that may twist and turn as one moves:

Concretely:

In
**twisted non-abelian generalized cohomology**
ncatlab.org/nlab/show/twis…
(see Sec 4 of: arxiv.org/abs/1207.0248)

a twisting τ
(of A-cohomology theory on some X )
is a bundle over X
with typical fiber A,

and

a τ-twisted cocycle
is a section of that bundle

Famous among twisted cohomology
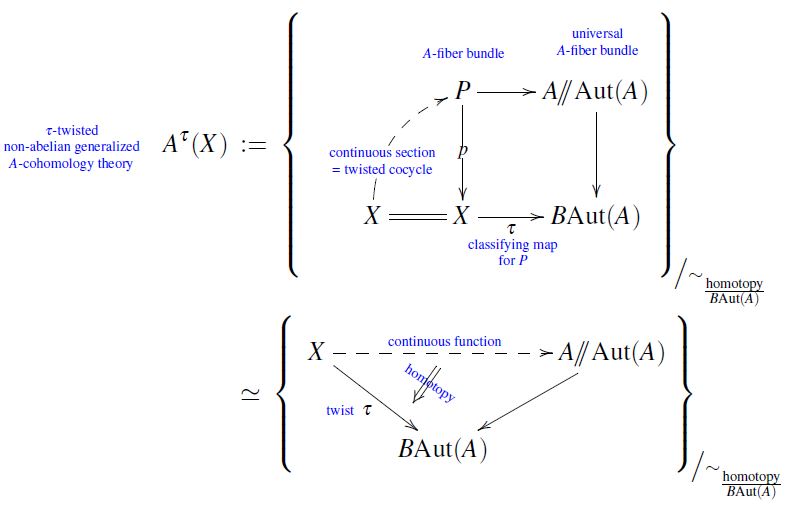
is *twisted K-theory* ncatlab.org/nlab/show/twis…
which fits into the scheme of twisted cocycles
as being sections of bundles of classifying spaces
in its formulation
as sections of bundles of Fredholm operators
due to Rosenberg doi.org/10.1017/S14467…

**Cohomotopy theory is twisted by sphere-bundles**
often called "spherical fibrations"
ncatlab.org/nlab/show/sphe…

A twisted cocycle in twisted Cohomotopy theory
ncatlab.org/nlab/show/twis…
is a section
of a spherical fibration.

Its cohomology class
is its homotopy class
as a section.

For example,
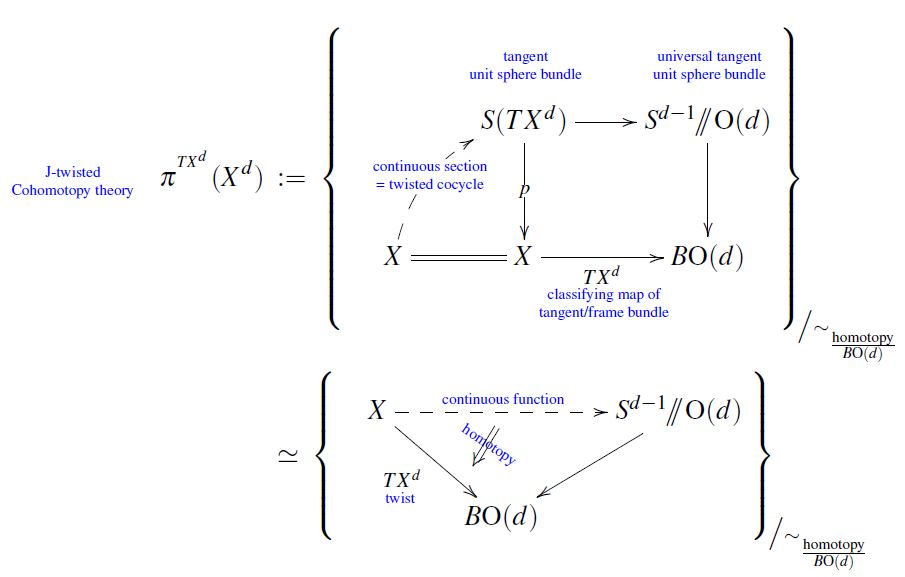
every Riemannian d-manifold
carries a canonical twist
for (d-1)-Cohomotopy theory:

given by
the unit sphere bundle
inside its tangent bundle.

In terms of classifying maps
for these bundles
this means twisting by
the **J-homomorphism**
ncatlab.org/nlab/show/J-ho…

Now recall that
before twisting
we had the quaternionic Hopf fibration
ncatlab.org/nlab/show/quat…
exhibiting a reflection of
(untiwsted) 7-Cohomotopy
into
(untwisted) 4-Cohomotopy.

It is interesting to ask
with which twists
this Hopf reflection can be compatible...

It turns out that
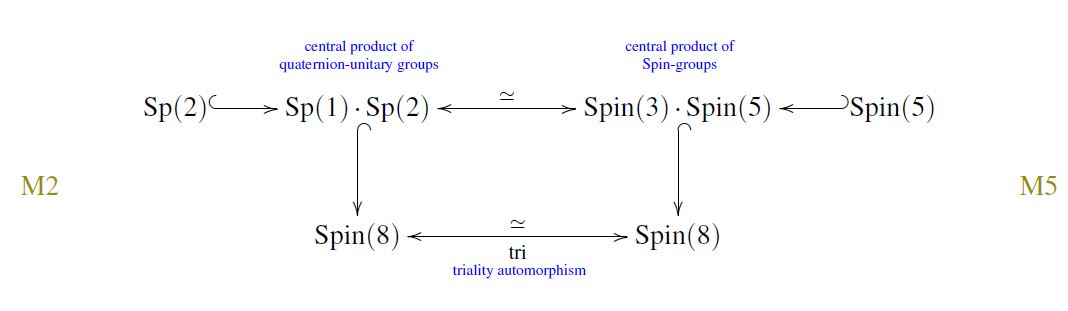
the **largest twisting group**
under which the quaternionic Hopf fibration
still induces a homomorphism
from twisted 7-Cohomotopy
to twisted 4-Cohomotopy
is the central product

Sp(1).Sp(2)
ncatlab.org/nlab/show/Sp(n…

of quaternion-unitary groups.

While the group

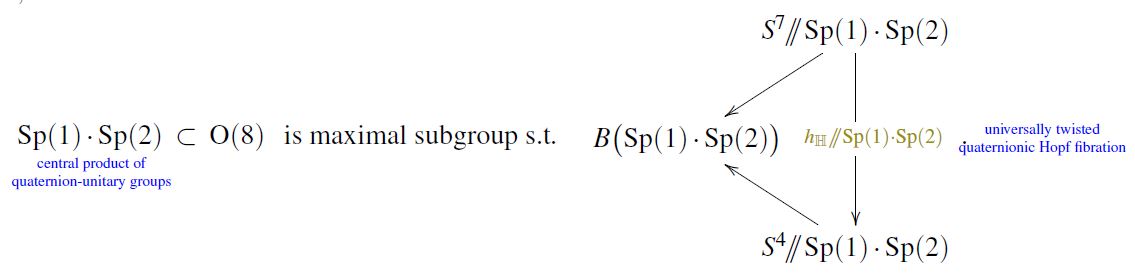
Sp(1).Sp(2)

is abstractly isomorphic to

Spin(3).Spin(5)

they are *distinct* as subgroups of Spin(8)
hence distinct as Cohomotopy twists.

BUT they transmute into each other
under (the forgotten corner of)
**triality**
ncatlab.org/nlab/show/tria…

We will focus attention now
on the twist subgroup

Sp(2) in Sp(1).Sp(2)
ncatlab.org/nlab/show/Sp(2)

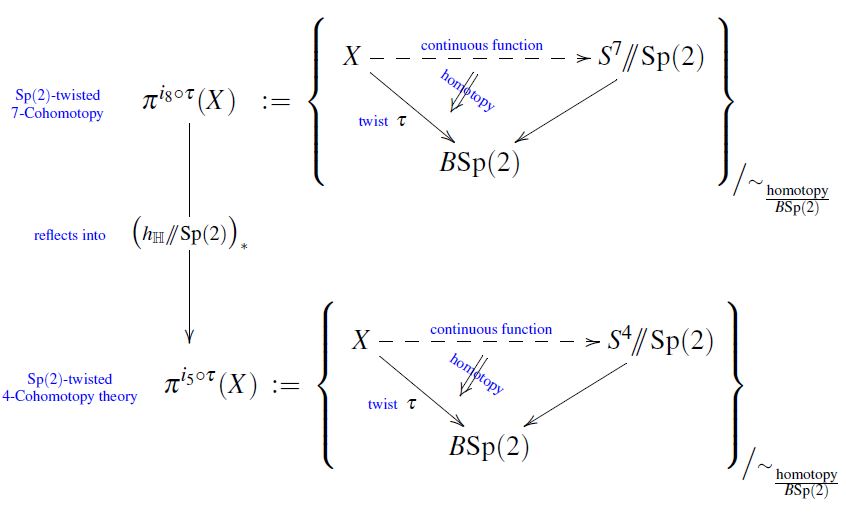
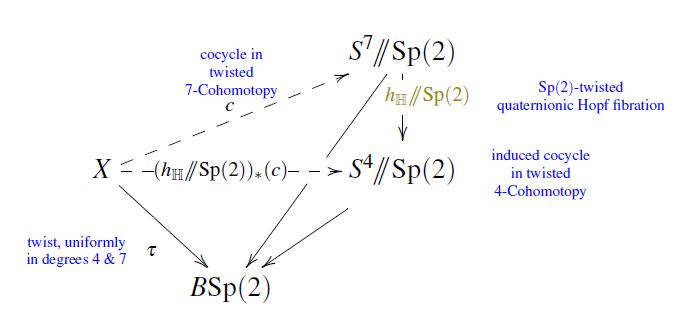
By what we just said,
the quaternionic Hopf fibration
is, in particular, Sp(2)-equivariant
and hence serves to transmute
Sp(2)-twisted 7-Cohomotopy
into
Sp(2)-twisted 4-Cohomotopy:

In conclusion so far
we have found that and how

the reflection
of 7-Cohomotopy
into 4-Cohomotopy

extends to

a reflection
of Sp(2)-twisted 7-Cohomotopy
into Sp(2)-twisted 4-Cohomotopy:

.
.
.
B R E A K
.
.
.
next time:

the cohomotopical Chern character
.
.
.