Thread by @pgroisma

Apolo, Dios de la música, se le presentó a Pitágoras y le dijo
Harás una escala musical con octava y quinta.
Y Pitágoras respondió
- Nochepuede
A lo que Apolo contestó
- No vas a empezar a joder de vuelta con lo de los irracionales, no?
Y Pitágoras: #TeRegaloUnTeorema

(sigue)

🗣️ Acordate de retwitear que si no Apolo te condenará a una vida disonante.

Queremos construir una escala musical con m notas. Tenemos que elegir qué notas incluir. La onda es, dada una frecuencia base (p. Ej 440 Hz, el LA), elegir qué otras frecuencias (notas) poner.

Ponele que queremos meter las que suenan lindo. La que más lindo suena es la que tiene el doble de frecuencia (o la mitad, si vamos para abajo). Tan bien suena que la llamamos octava y le ponemos el mismo nombre. (Ej LA 220Hz, LA 880 Hz).

La siguiente en orden de lindura es la frecuencia triple.
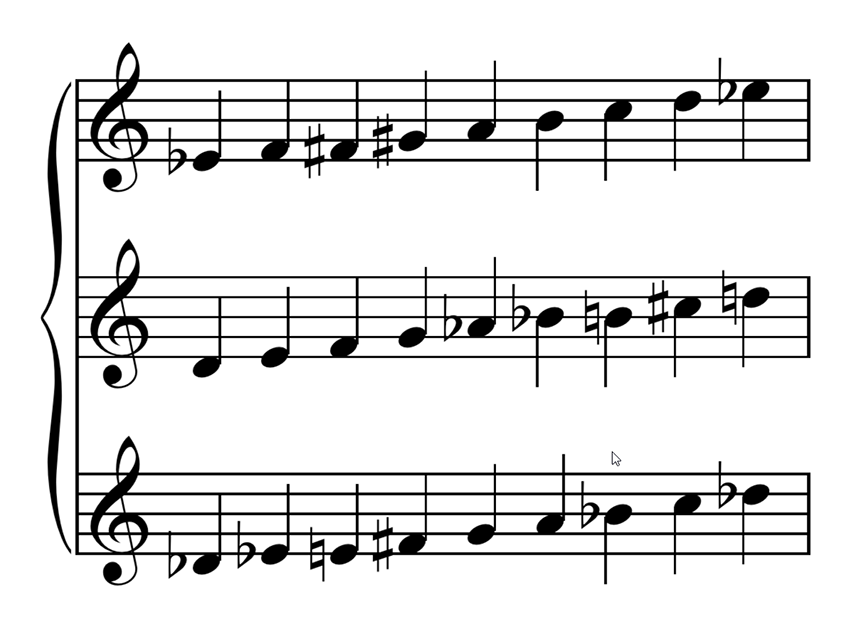
Entonces lo que Apolo le pidió a Pitágoras es una escala en donde por cada frecuencia que aparezca, aparezca tmb el doble y el triple de ella.

Si arrancamos con DO, la quinta es SOL y la octava el siguiente DO. La frecuencia triple está más allá de la octava. Si queremos meterla entre un DO y el siguiente, tenemos que dividir por 2 y nos da 3/2.

¿Se puede?

🅃🄴🄾🅁🄴🄼🄰 🄳🄴 🄸🄼🄿🄾🅂🄸🄱🄸🄻🄸🄳🄰🄳 🄳🄴 🄻🄰 🄴🅂🄲🄰🄻🄰 🄼🅄🅂🄸🄲🄰🄻 🄿🄴🅁🄵🄴🄲🅃🄰.

No, no se puede.

🅳🅴🅼🅾🆂🆃🆁🅰🅲🅸ó🅽

Para pasar de una nota a la siguiente hay que multiplicar por un número fijo que vamos a llamar r. Multiplicar siempre por r a la frecuencia corresponde a subir un tono siempre igual.

Entonces si la escala tiene m notas y nuestra frecuencia base es C, tiene que valer

Cr^m=2C, o lo que es lo mismo, r^m=2

(acordate que el ^ es "elevar a la")

Ahá, entonces r=2^(1/m).

La quinta, que es 3/2 de C nos queda entre C y 2C así que va como piña. Si queremos que esté esta frecuencia, necesitamos que exista un número natural k menor que m tal que

r^k = 3

Y como r=2^(1/m) nos queda

2^(k/m) = 3

O lo que es lo mismo

k/m = log_2(3)

Así que esto se va a poder hacer sólo si el logaritmo en base 2 de 3 es un número racional. Pero adiviná qué? No lo es. No se lo digas a nadie. Acordate que a Hippasus lo ahogaron los Dioses por esto mismo. en.wikipedia.org/wiki/Hippasus

Para ver que el logarítmmo en base 2 de 3 es irracional hacemos como cuando demostramos que raíz de 2 es irracional

https://twitter.com/pgroisma/status/1142491377110007809?s=20

, pero acá es más fácil.

Suponete que sí lo es. Es decir que existen números naturales k y m tales que

k/m = log_2(3)

O sea,

2^(k/m)= 3

Entonces

2^k=3^m

Pero el número de la izquierda es par y el derecha es impar. Eso es absurdo! O sea que no existen tales k y m.

Conclusión: no se puede hacer una escala musical con una cantidad finita de notas y que tenga la octava y la quinta justa.

#TeRegaloUnTeorema.

Ah! La que más usamos nosotros, tiene 12 notas y la “quinta” está en el lugar 7,

7/12=0,583333333333
y
log_2(3) – 1 = 0,584962501

No es una quinta “justa”, pero no está tan mal. Por eso usamos 12 notas!

Buen Viernes y que la (buena) música los acompañe!