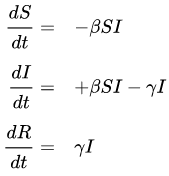Acabo de leer este tuit via @pmarsupia y voy aprovechar para hablar un poco del R0 de una enfermedad
El grupo S, el grupo I y el grupo R. Ya veis que en matemáticas no nos rompemos la cabeza poniendo nombres a los conjuntos, estamos a otras cosas.
Ante determinadas enfermedades no todos somos susceptibles de enfermar.
Yo no soy susceptible de enfermar de algo que ataque solamente a la próstata. Creo.
Y, MUY IMPORTANTE, tampoco son susceptibles de enfermar las personas VACUNADAS.
Y, como en el caso de S, en cada instante de tiempo, t, tendremos un valor I(t) que nos indica cuántas personas infectadas por la enfermedad hay en ese momento.
Ya conocéis la leyenda sobre el origen del ajedrez y los granos de arroz, ¿no?
mati.naukas.com/2012/04/01/gau…

¿Cómo te quedas?
En otro caso, lo único que podemos hacer es aislar con seguridad a los infectados.
Y que es precioso mirar el mundo a través de las matemáticas :)