Thread by @bluecology

Just got my hands on the classic Generalized Additive Models book by Wood (Edn 2, 2017). #rstats mgcv is a deep package, here's some tips 1/n

There's more types of smoothers than pokemon, if you're just fitting
gam(v ~ s(x))
You are missing out!
2/n

If you don't have the book type ?smooth.terms in R with mgcv loaded and you get a nice summary
3/n

v ~ s(x, bs = "cs")
gives a 'smoothing basis' with a cubic spline with shrinkage.
Shrinkage means they will 'shrink' to a flat line if the term isn't important.
So you get model selection 'for free' (no AIC!)
4/n

(AIC by the way is conceptually tricky with GAMs, my students are finding cs much easier)
5/n

m1 <- gam(v ~s(ID, bs = "re"))
Gives you a random effect with groups, similar to lme4 or nlme, without having to use those packages.
Then do gam.vcomp(m1) to get the rand effect variances
6/n

v ~ s(x, y, bs = "sos") gives you a spline on a sphere, think global scale modelling
(image from mfasiolo.github.io/mgcViz/referen…)
7/n

bs = "mrf" and bs = "gp" give you random fields, which are pretty handy for modelling spatial dependence.
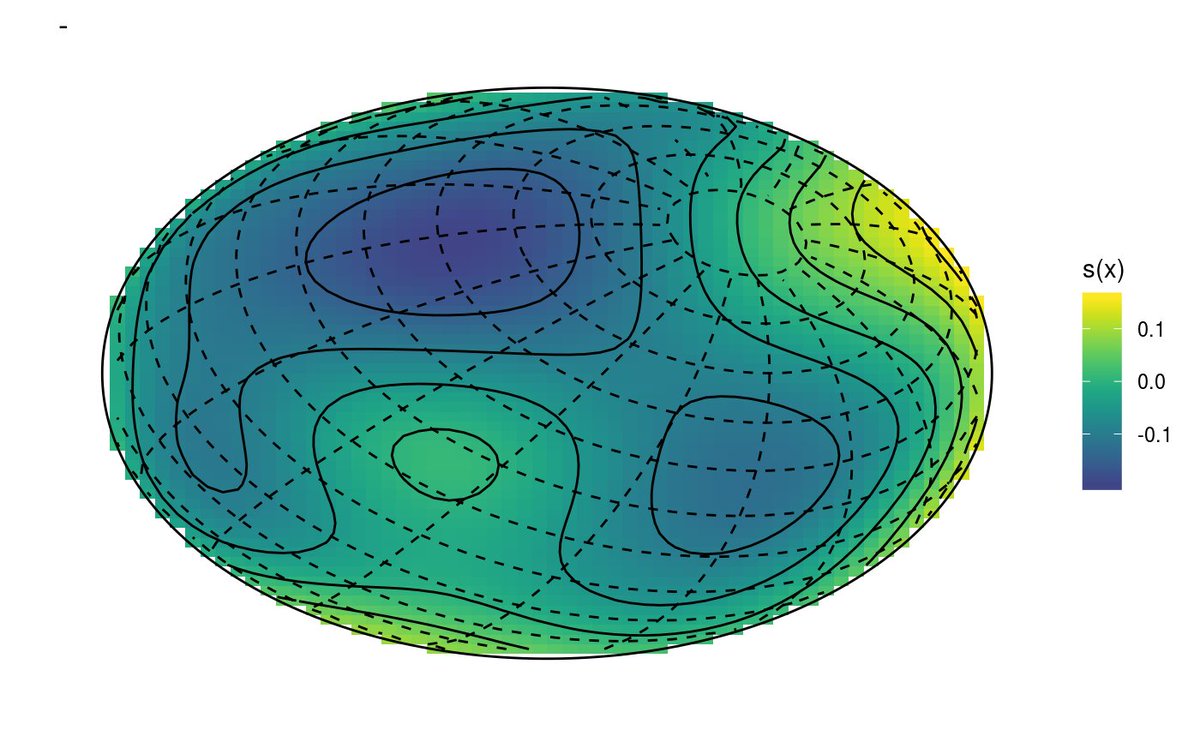
MRF is for dependence between neighbouring regions, gp for coordinates (e.g. x,y)
8/n

It also turns out there is a mathematical equivalence between GAMs and Bayesian analysis. So your GAM is 'Bayesian' in a sense. Want Bayesian credible intervals?
Then use
predict.gam(m1, type = "lpmatrix)
see ?predict.gam for an example
9/n

(doing my best to summarize why:
GAM smoothers have a penalty. And what is a penalty if not a Bayesian prior?)
10/n

Of course if you want the full flexibility of a Bayesian GAM then Wood has written jagam to create JAGs code for your GAM formula and also recommends readers see pkgs BayesX or INLA
11/n

Here's one of my favourite sections.
What I gather it means is that clever math can speed things up for large data sets. Fortunately Wood has summarized all that with one elegant function:
bam(v ~ s(x))
Use it if gam is too slow for you
12/n

gotta go teach #rstats now, more later!

You can model variation in the response variance with covariates using family=gaulss or gevlss
13/n

You can partition smooth interactions into main and interactive effects with te() and ti(), which is useful for testing whether an additive model is sufficient
14/n

Did I mention smoother interactions?
s(x, by = groups)
fits one smoother per group, if groups is a factor.
s(x, by = groups, id = "A")
does the same, but will use the same (not variable) smoothing factors for each group
15/n

Ok, this is really cool:
if you do
s(x, by = y)
and y is numeric, it fits a smoother where the effect of x varies with y, e.g. you can do 'geographic regression', where an effect varies across space
16/n