Thread by @simon_tardivel

Ah la lunar gateway, cette future (ou pas) station spatiale près de la Lune, sur sa fameuse orbite baptisée "NRHO".

NR à quoi?!

Allons-y, aujourd'hui les orbites de Halo: qui sont-elles ? quels sont leurs réseaux ? doit-on en avoir peur ? Un thread garanti sans #COVID19 !
👇👇

Pour les impatients, on commence par la fin. 😃

Comment un tel mouvement est-il donc possible ?!

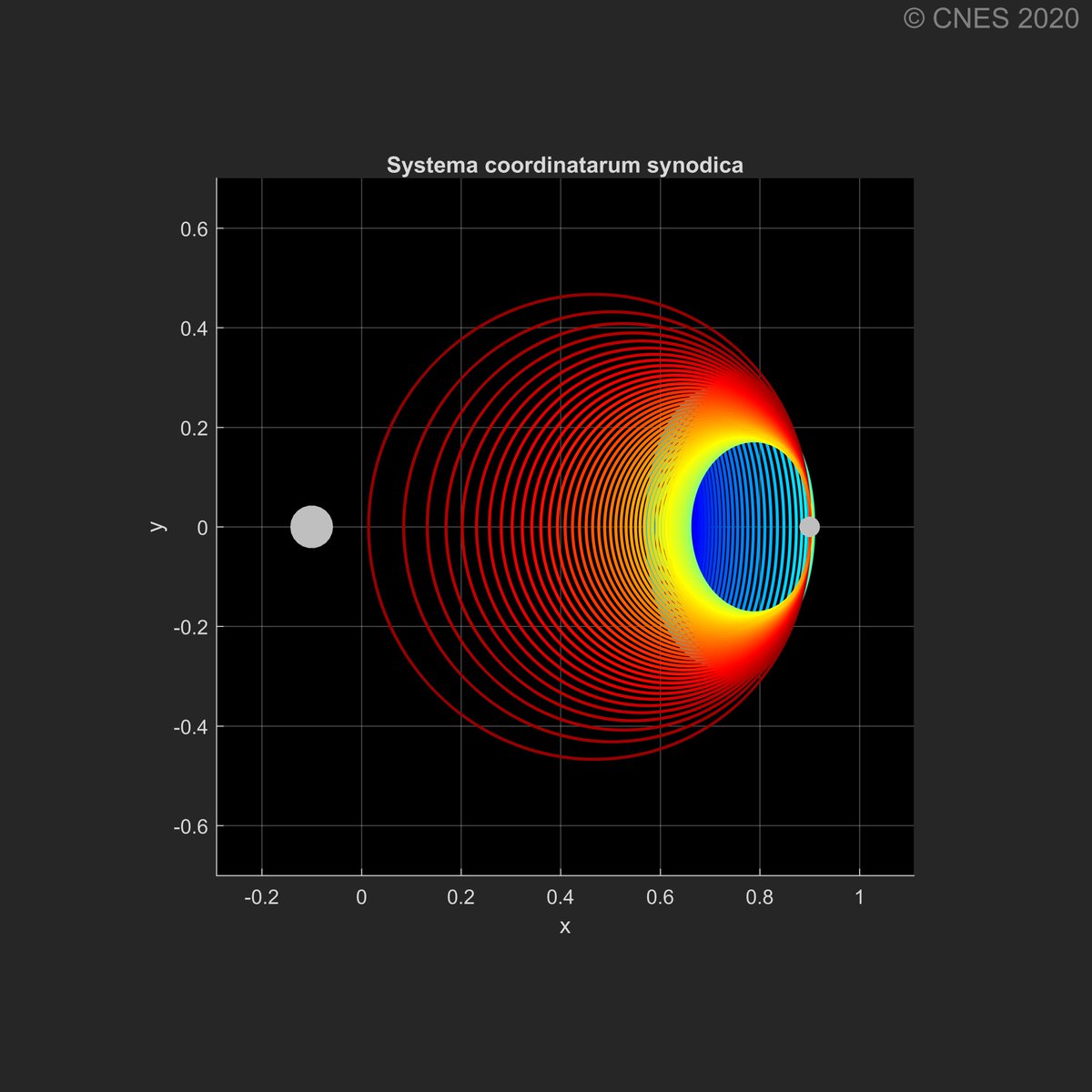
Pour rappel, nous sommes dans un système à 3 corps (restreint, cr3bp pour les intimes). Par exemple la Terre et la Lune, ou Pluton et Charon, etc. (pour les pro, ici mu = 0.1 😉)

Dans un thread précédent, je discutais des orbites autour des points de Lagrange, ces points qui flottent entre les astres. C'était plutôt plan-plan comme discussion : on restait dans le même plan (!) de l'orbite des 2 corps, qu'on regardait de haut 🧐

https://twitter.com/simon_tardivel/status/1233413824172167168

Pour parler des orbites de #halo, il faut commencer à regarder le problème en 3d. On reste autour d'un point de Lagrange mais on sort du plan. Il est temps donc de regarder ce qui se passe sur l'axe z.

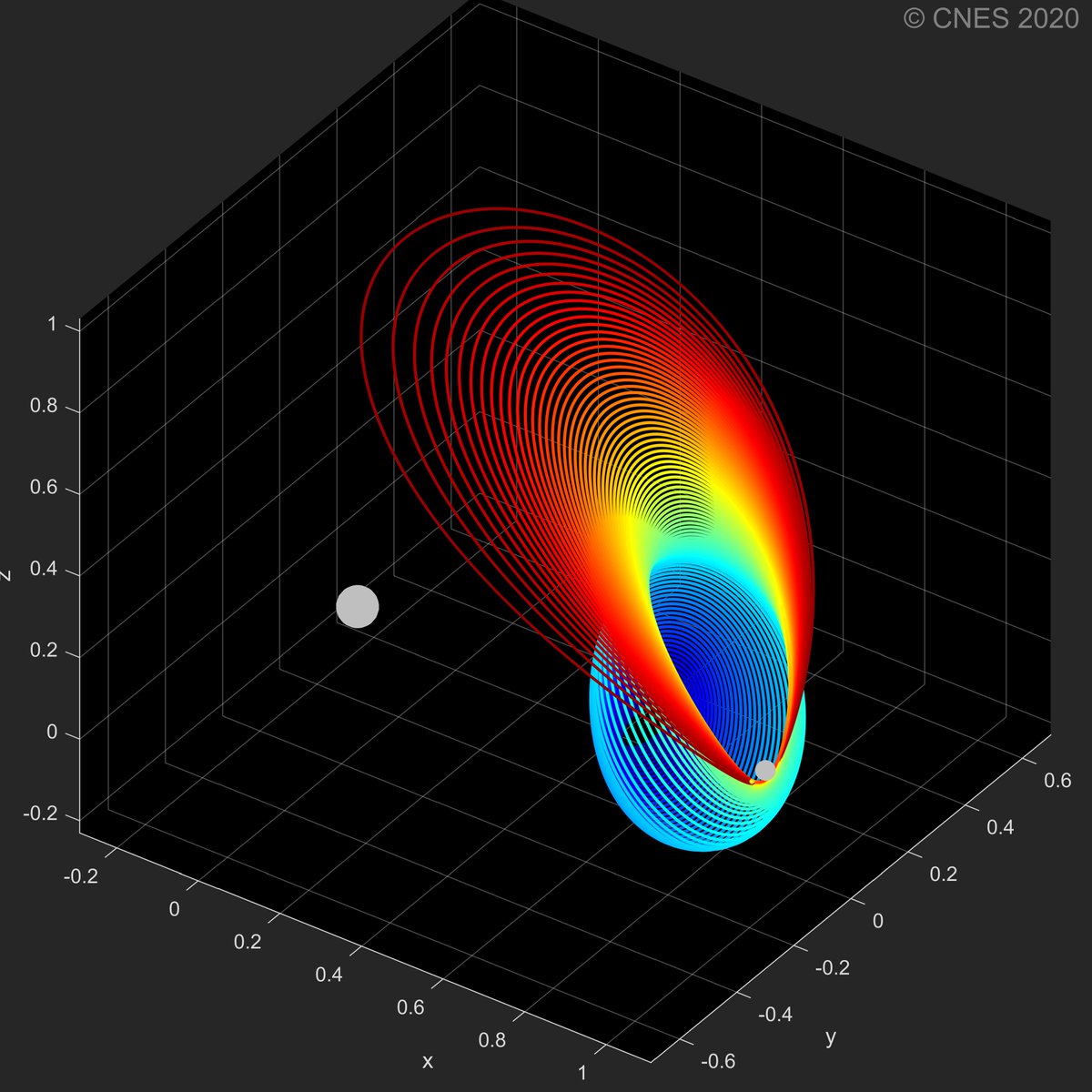
Bienvenue dans la 3ème dimension 😰

Les orbites de halo, pour les présenter correctement, il faut rentrer un petit peu dans les détails. Promis pas techniques et les animations seront là mais avant ça... faut qu'on cause 😐.

Mais ne t'inquiète pas, ça va bien se passer. Bien se passer. Ne t'inquiète pas.

Dans le problème à 3 corps, on montre rarement l'axe z. La raison : il ne s'y passe pas des trucs très intéressants. Ça oscille de haut en bas, doucement, sans vraiment influencer ce qui se passe dans le plan. Le plan c'est donc ce qui reste le plus intéressant en général.

Mouais sauf que dire ça, c'est un peu trop simplifier le problème. Il peut quand même s'y passer des trucs, et ça peut avoir des grosses conséquences. Justement, une des conséquences c'est les orbites de halo. Halo comme ça :😇

Et non, ça n'est pas (du tout) une référence à ça :

Le principe est simple. On avait des orbites planaires (cf. autre thread) qui s'appellent des orbites de "Lyapunov". Elles avaient une certaine période qui dépendait de leur taille. L'oscillation en z a aussi une certaine période.🤔
Est-ce qu'on pourrait pas les... synchroniser ?

Oui on peut ! Et on prouver, mathématiquement, que "il existe au moins une famille d'orbite périodique en 3d autour d'un point de Lagrange". Donc pas juste une orbite, toute une famille d'orbite ?!
👏👏👏
Magnifique !

(dsl je fais dans la facilité sur les GIFs aujourd'hui...)
Sauf que là, le mathématicien, il a fini son boulot : il a prouvé que ça existait. Mais le reste il s'en fout, les trouver c'est pas son job ! C'est le nôtre. Donc il ajoute : "et bonne chance mon coco" et il se barre.😟

C'est donc dur de les trouver ces orbites de halo... Dans le plan on partait du point de Lagrange et on faisait grossir notre orbite. Mais là, ça marche pas parce qu'il faut que l'orbite de halo ait une taille minimum : en dessous il n'y a pas d'orbite de halo possible !

Trouver notre orbite de halo revient donc à trouver une aiguille dans une botte de foin. On connait ni sa taille, ni (vraiment) sa forme, et en plus elle est instable (on en parlera plus tard).

Et le pire, c'est que la botte de foin elle existe en 6 dimensions en fait ! 🥴

Hé oui, 3 positions (x,y,z) et 3 vitesses (sur x,y,z) ça fait 6 dimensions en tout. Mais bon le mathématicien nous a laissé un indice de taille : avec une phrase énigmatique, mystique même...

🧙‍♂️"Ces orbites de halo sont une *BIFURCATION* des orbites trouvées dans le plan".

On pourrait faire un thread entier sur ce concept mystérieux de bifurcation. 😯

Pour nous et pour l'instant, on se contentera de dire: ici, ça veut dire que nos orbites de halo "se détachent" d'une certaine orbite du plan.

La famille des orbites de Halo va donc sortir du plan, mais en cherchant bien, on doit pouvoir trouver une halo qui se colle autant que l'on veut 😏 à une orbite du plan. Et ensuite on peut la rendre de plus en plus verticale, et on obtient toute la famille des halos.

Dernier détail: le problème est symétrique en haut et bas - on parle plutôt de Nord et Sud d'ailleurs ici. Je vous montrerai des orbites "nord" et il suffit de symmétriser pour obtenir celles du sud.

On a fini avec les détails semi-teshniques ! OUF !

Des gens très malins ont fait ça à partir des années 70-80, et on a bien compris comment trouver des halos désormais. Voilà donc une orbite de halo typique qui fait partie de cette grande famille.

Ca parait pas trop choquant... jusqu'à ce que la perspective change ! 😲

La famille des orbites de halo commence quand on sort du plan et se termine quand elle atteint le plus petit des deux corps (la Lune par exemple). Entre ces deux extrêmes, une infinité d'orbite ! 🤓

Voilà 4 images de différents angles de vue, pour bien se représenter la famille.

Pour ceux qui sont là pour les animations : c'était ma petite animation mystère du weekend. Et nombreux sont ceux qui avaient trouvé de quoi il s'agissait ! 👏👏👏

https://twitter.com/simon_tardivel/status/1239232538251575300

On peut donc passer aussi près du petit corps que l'on veut. Mais pour ça il faut aller chercher loin dans la famille, il faut partir de très haut. Et alors on obtient une orbite allongée, quasiment rectiligne.

Autrement dit une "Near Rectilinear Halo Orbit".

N R H O

Donc :
- Les orbites de halo? c'est des orbites qui sortent du plan.

- Leurs réseaux? C'est toute une famille, bien peuplée !

- Faut-il en avoir peur ? les NRHO à froid, oui, c'est chaud...

- Sont-elles des zones à risque du #COVID19? non mais #RESTEZCHEZVOUS quand même !

Je continuerai ce thread plus tard avec de nouvelles anims. N'hésitez pas à poser vos questions et à me dire ce qu'il vous intéresserait de voir/savoir à ce sujet. 🤓

Pour l'instant, j'ai une journée de télétravail qui m'attend comme le reste du @CNES et vous aussi j'espère !

On va continuer ici, avec le grand jeu du soir !!!
👇

https://twitter.com/simon_tardivel/status/1239972334993199105