Thread by @drjwdietrich

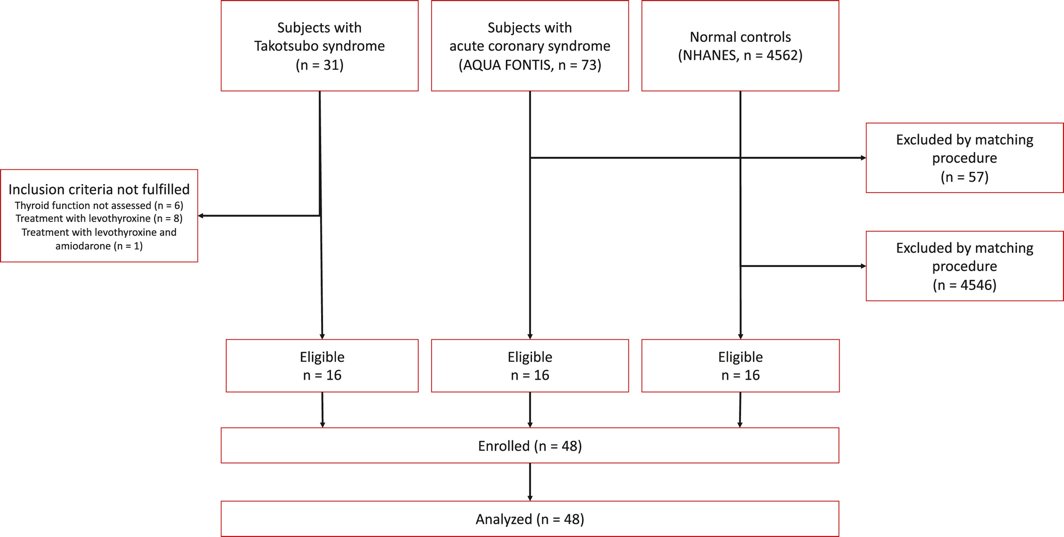
1/n: On the occasion of current discussions on testing strategies in #COVID19 let's make a short tweetorial on medical decision making (a branch of biomedical cybernetics, which is underestimated but has enormous impact). #cybernetics #biocybernetics #DecisionTheory

2/n: #Sensitivity, also known as "true positive rate" (TPR) is the fraction of the number of diseased subjects with positive test divided by all diseased patients. Since in both numerator and denominator are pure counts it is independent of the prevalence of the disease:

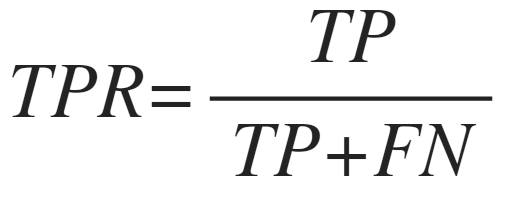
3/n: Likewise, the true-negative rate (TNR), the ratio of true negatives to the sum of false positives and true negatives, is independent of the prevalence:

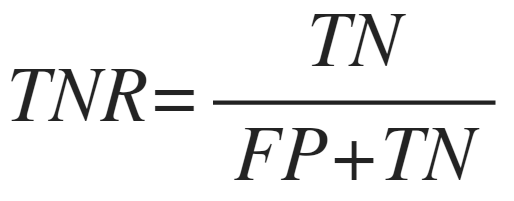
4/n: Similar considerations apply to the false negative rate (FNR) and the false positive rate (FPR). Again TN, TP, FN and FP denote the numbers of true negative, true positive, false negative and false positive subjects.

5/n: The true-negative rate (TNR) is also referred to as #specificity of a test.

Predictive values provide information on the post-test probability of disease. The positive predictive value is the ratio of true positives to the sum of true positives and fals positives. It delivers the fraction of patients with positive test who also have the target condition.

7/n: The positive predictive value depends on the pre-test probability (i.e. the #prevalence) of disease. This is also one of the major drawbacks of this ratio, since it cannot be used to compare different test strategies without additional information on epidemiology.

8/n: Similarly, the negative predictive value is the fraction of non-diseased subjects among those with negative test resuts. Again, it depends on prevalence.

9/n: Positive and negative likelihood ratios (LR+ and LR-) denote the ratio of the probability of a positive (or negative, resp.) finding in diseased patients to the probabiltiy of this same finding in non-diseased subjects. #Likelihood_ratio.

10/n: #Likelihood_ratio⁣s are independent of the pretest probability. Therefore, they are a universal measure and the preferred figure to compare the performance of diagnostic tests.

11/n: However, if required, the post-test probability can be calculated from #likelihood_ratio⁣s. The way is the odds ratio form of #Bayes' theorem:
post-test odds = pre-test odds x likelihood ratio.

12/n: In this way, #Likelihood_ratio⁣s provide a welcome simplification of the standard approach of using #Bayes' theorem to calculate the post-test probability:

13/n: This and other useful information may be learned from the excellent book "Medical Decision Making" by Harold C. Sox, Michael C. Higgins and Douglas K. Owens. onlinelibrary.wiley.com/doi/book/10.10… doi.org/10.1002/978111… thalia.de/shop/home/arti…