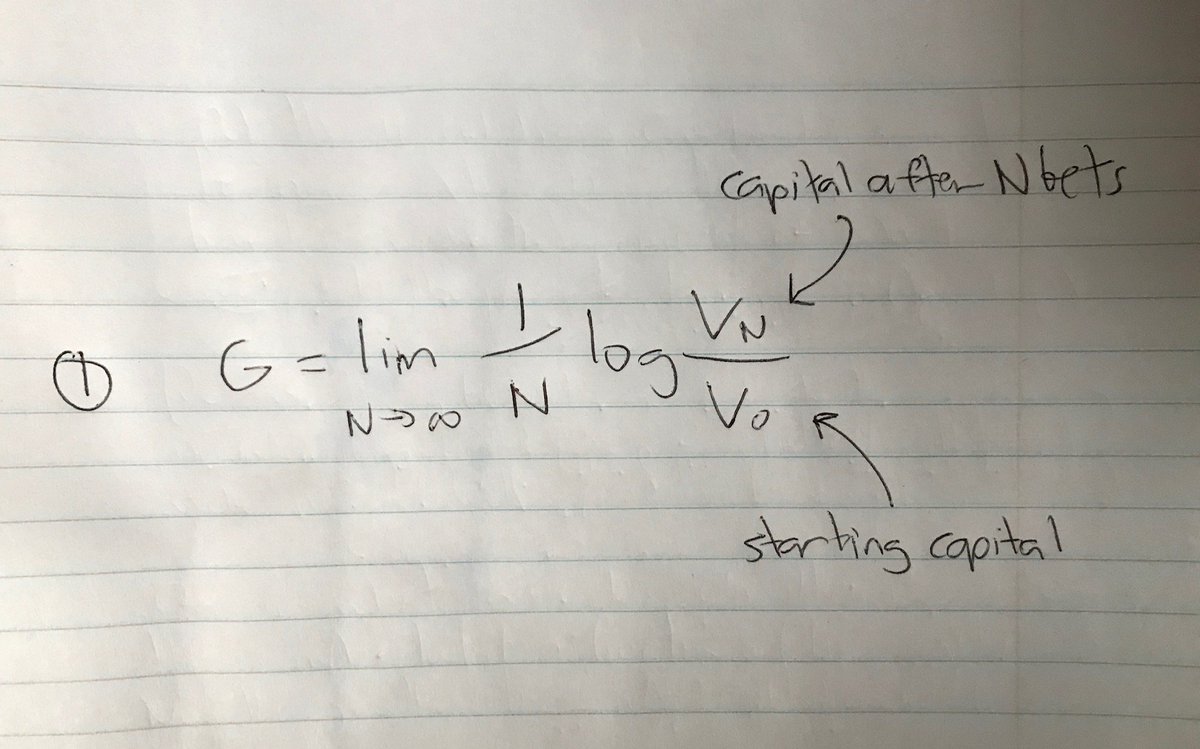
So the alternative is for the gambler to bet a fraction of his capital each time. Now we can express the growth of the gambler's capital as:
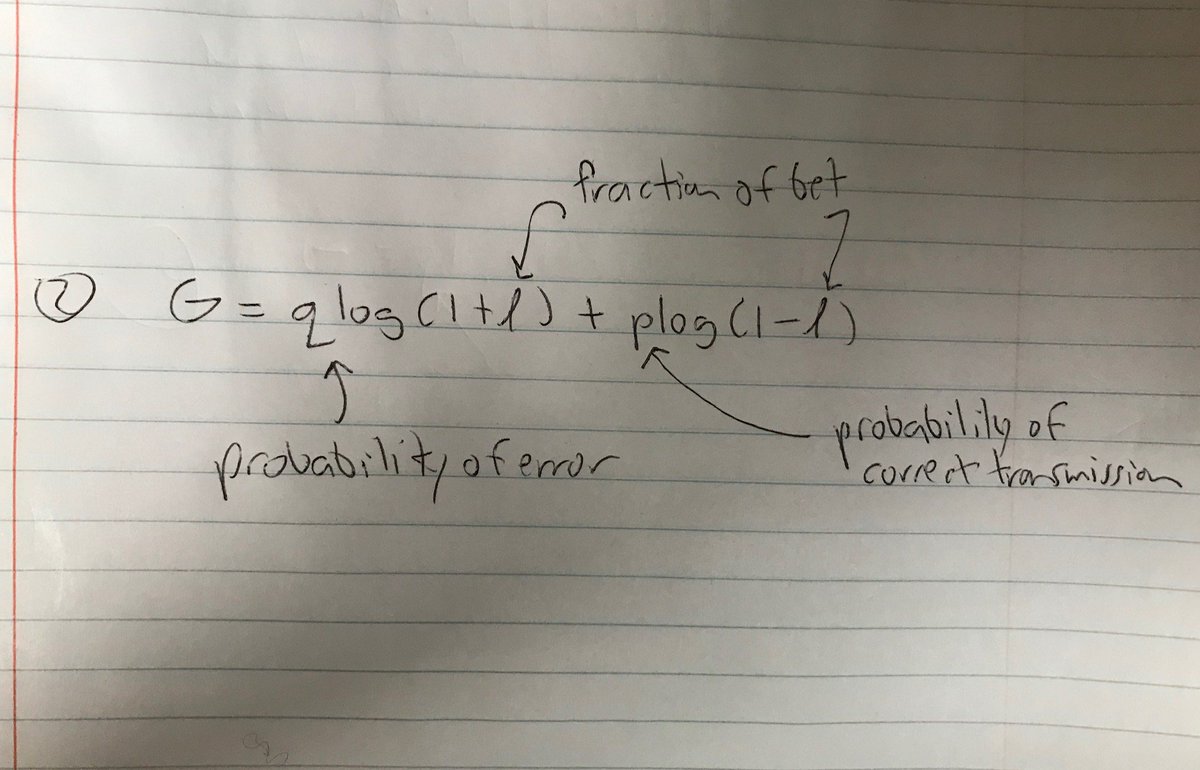
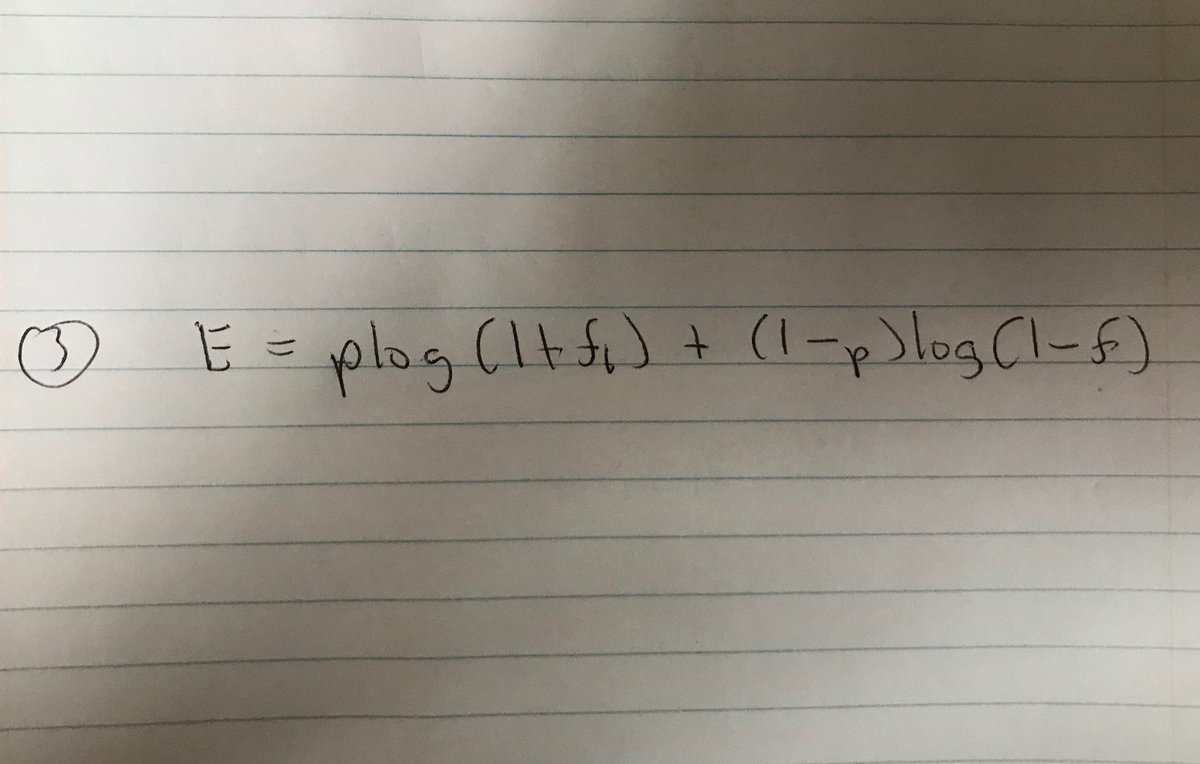
So, what happens when we maximize the gambler's growth of capital? By differentiating equation 3 and setting to 0:
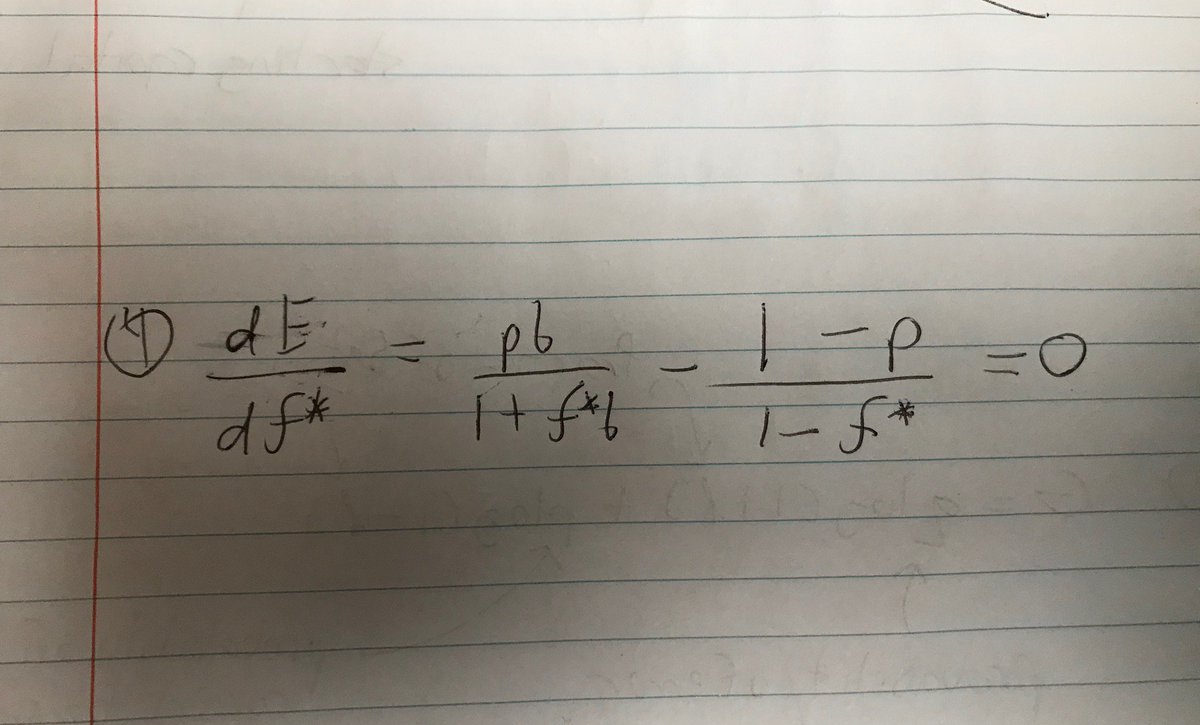
Apologies for the Tweet storm.
















