


This is not to say all investigators are always on the up and up - I have absolutely worked with would-be authors that wanted to use QRP's - only to say that this is not reflective of how...
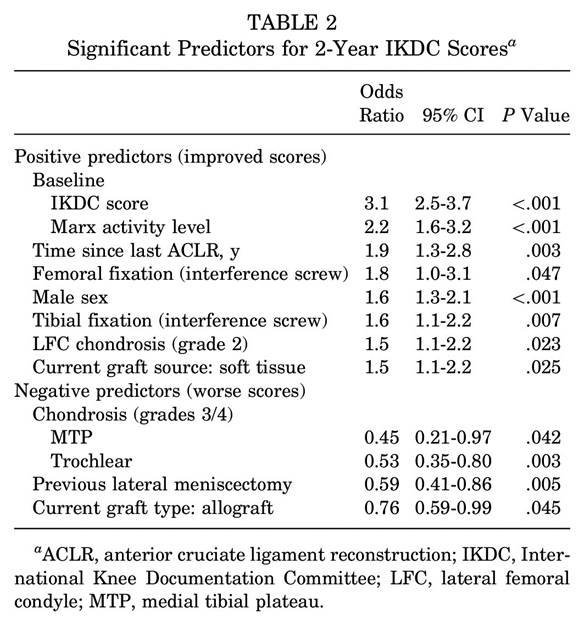
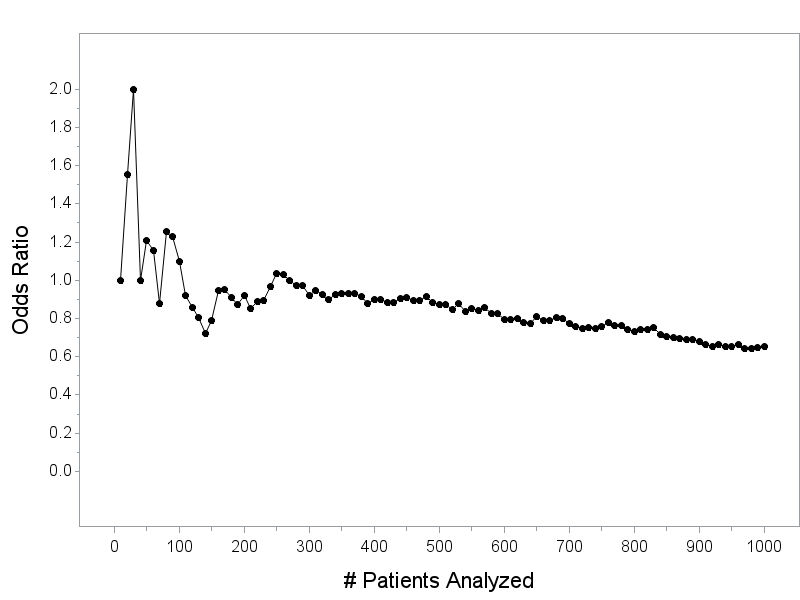
Trials that show big effects and run to completion can’t be trusted because it’s not plausible that the effect size could be that big!
Therapies that haven’t been tested in trials shouldn’t be adopted without high-quality evidence!
I think this is important because perpetuating myths about trial design and statistics undermines faith in legitimate efforts to generate high-quality evidence because people misunderstood a half-truth they read in a blog post somewhere.