Thread by @e_goberna

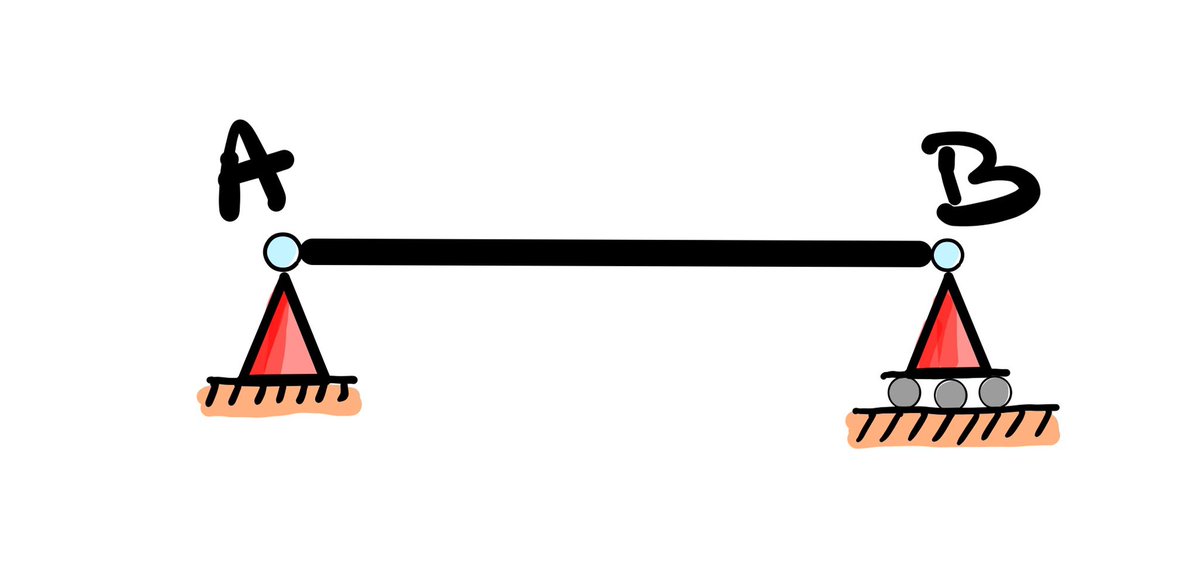
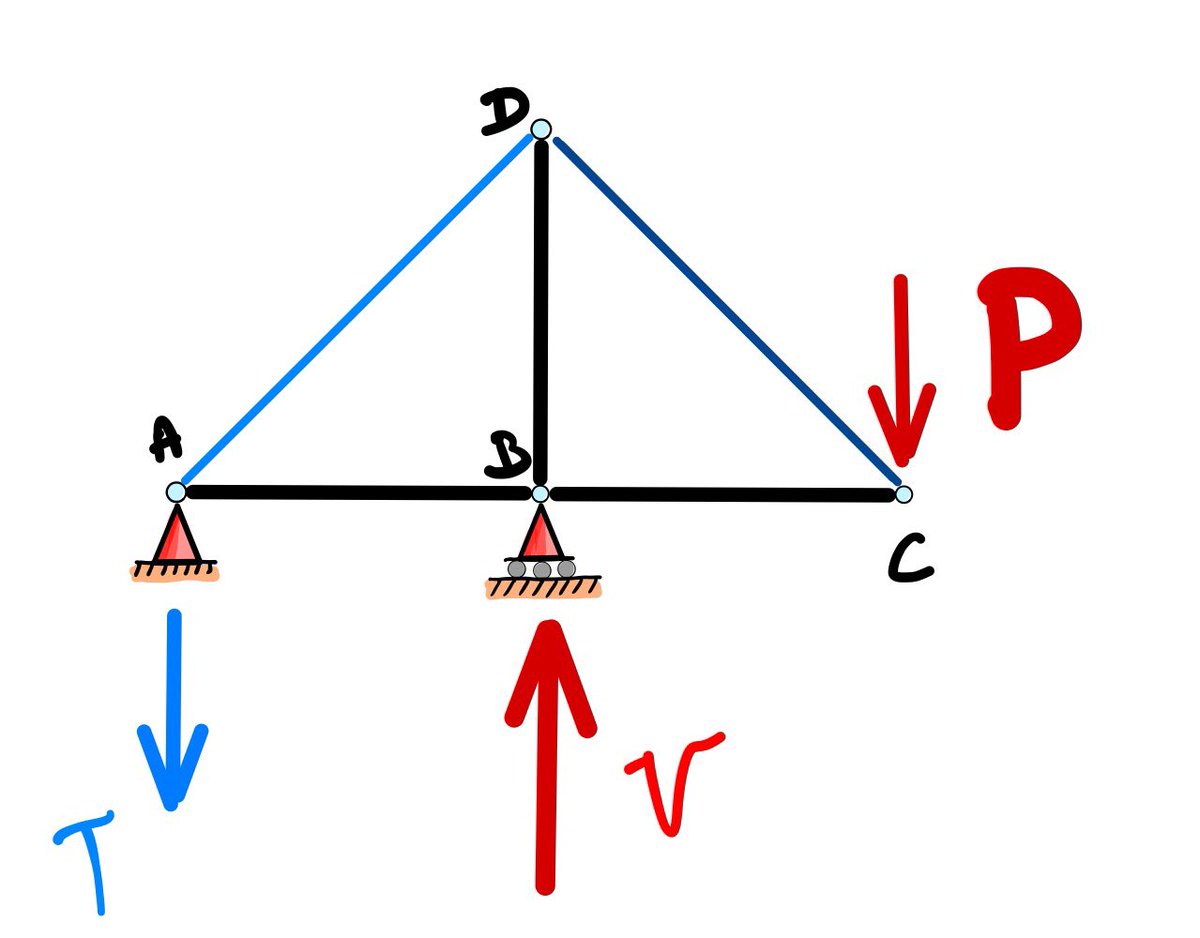
Hoy me voy a #Turquía para hablar de unos #puentes muy especiales. Hilo va 👇

#puentes, #estructuras, #Ingeniería, #bridges, #structures, #Engineering , #Historia

Mimar Sinan (1490-1588) fue el arquitecto principal del Imperio otomano, sobre todo en tiempos de Solimán el Magnífico, sultán y enemigo sempiterno de Carlos V (al menos uno de ellos).

Sinan pertenecía a una familia cristiana de la Capadocia. De niño fue separado de su familia y obligado a convertirse al Islam y a servir como Jenízaro (militar de élite del Imperio otomano) para Solimán.

Destacó como ingeniero militar haciendo puentes, murallas, acueductos….Cuando tenía unos 50 años fue nombrado arquitecto principal de Solimán. En esa época se explayó como constructor de algunas de las mezquitas más impresionantes de #Estambul.

También hizo baños públicos, colegios, mausoleos, palacios... Era contemporáneo de Leonardo da Vinci, Miguel Ángel, Juan de Herrera. Su historia y su obra son magníficas. Los casi 90 años de edad que vivió dieron para mucho.

Me interesa mucho su figura como constructor de #puentes y acueductos. Os pongo algunos ejemplos.

Este acueducto es genial. Está cerca de Estambul. Es de origen bizantino (el Impero bizantino era, por así decirlo, el heredero del Impero romano en oriente hasta que llegaron los otomanos). El acueducto fue destruido por una avenida de agua en 1563.

Sinan se hizo cargo de su reconstrucción en 1564. Él hizo esos contrafuertes para que el acueducto fuera resistente a los embates laterales de los sismos tan comunes en #Turquía.

google.es/maps/@41.12261…

Este puente sobre el río Drina en Višegrad, Bosnia y Herzegovina, es magnífico. Su nombre, Puente Mehmed Paša Sokolović.
Fue terminado en 1577. Por contextualizar, la batalla de Lepanto (Juan de Austria, Cervantes….) ocurrió en 1571.

google.com/maps/@43.78319…

Mehmed Paša Sokolović fue, al igual que Sinan, separado de su madre en este punto del río para ser reclutado como Jenízaro. Con los años, Mehmed se convirtió en un importante visir (ministro de la época) y mandó construir un puente en ese mismo lugar.

Qué simbólico! El punto de la separación se convertiría en punto de unión para siempre.

El puente, en un lugar estratégico, fue parcialmente destruido durante la Primera Guerra Mundial. Tal y como se ve en la imagen, se salió del paso con un tramo en arco metálico.

Durante la WWII el puente también fue dañado. Precisamente, durante esa época, el Ivo Andrić escribió en Belgrado la novela “Un puente sobre el Drina”. El Premio Nobel de Literatura no tardó en llegar.
Podcast de @rtve sobre la novela:
rtve.es/alacarta/audio…

Otro puente de Sinan. Mirad este puente de piedra sobre el río Bistrica, en Prizren, Kosovo. Me llama la atención ese ¼ de arco para materializar el aliviadero de la izda. en la foto (margen derecha del río).

google.com/maps/@42.20964…

Mimar Sinan también creó escuela! Un discípulo suyo, Mimar Hayruddin, construyó este puente que nos resulta muy familiar a los españoles. El puente de Mostar, Bosnia y Herzegovina, sobre el río Neretva.

Aquí un plano del puente de Mostar. Vaya Joya.

Sinan hizo más puentes, si bien destacó como constructor de mezquitas (más de 90!).

También trabajó en el diseño de su tumba en este rinconcito de #Estambul. 90 años dan para mucho.
google.com/maps/@41.01733…

Los #puentes unen culturas (además).

Espero que os haya gustado. :-)