Thread by @a_berut

Attention, il parait même que certaines personnes ont trouvé des traces d'éthanol dans les vins non-bios !!! Alors que l'éthanol est classé "cancérogène pour l'homme (classe 1)" par le CIRC !!! 🙃
fr.wikipedia.org/wiki/Liste_des…

External Tweet loading...
If nothing shows, it may have been deleted
by @AntoineTilloy view original on Twitter

Bon, je me moque (c'est pas gentil), mais je vais quand même vous expliquer pourquoi je trouve que cette étude (gavinpublishers.com/articles/Resea…) sur "le goût des pesticides" dans le vin n'est pas terrible.

Déjà, elle est publiée dans un journal qui figure sur la "liste des journaux prédateurs" de Jeffrey Beall. C'est-à-dire les journaux qui sont suspectés de publier plus ou moins n'importe quoi tant que les auteurs payent des frais de publication.

(Ça ne veut pas évidemment pas dire qu'il ne peut pas y avoir de bons papiers dans ces journaux, mais en moyenne, ce ne sont quand même pas les meilleurs articles qui y sont publiés...)

Ensuite, quand on lit les explications, il y a un certain nombre de choix discutables, voire difficilement justifiables.

Par exemple, les auteurs ont fait goûter des vins bios et non-bios (censés être équivalents par ailleurs) à des professionnels, et ont montré que dans 77% des cas ils ont préféré le bio.
Sauf que l'étude a été réalisée en simple aveugle, pourquoi ?

Le standard pour ce genre d'étude c'est le double aveugle (ni la personne qui sert le vin, ni la personne qui le goûte ne sait ce qu'il y a dans les verres), pour éviter d'influencer inconsciemment le goûteur.
Et en plus rien n'empêchait ici de faire du double aveugle...

(c'est important, parce qu'on se rend compte que pour plein de choses, notamment le vin, on peut être influencé par des facteurs extérieurs, par exemple, une étude a montré qu'un même vin vendu plus cher, ait mieux apprécié par les gens qui le buvaient : pnas.org/content/105/3/…)

(dans un autre registre, une étude a montré que contrairement à ce qu'affirmaient beaucoup de violonistes, ils sont incapables de reconnaître la supériorité d'un Stradivarius s'ils ne savent pas que c'en est un : pnas.org/content/109/3/…)

(et évidemment, dans des domaines comme vin, ou les violons de collection, où certaines pièces valent des fortune de part leur rareté et leur prétendue supériorité, il n'y a pas que la qualité intrinsèque du produit qui rentre en ligne de compte quand il s'agit de "tester")

Ensuite, l'étude a testé la présence de 250 pesticides dans les vins bios et non-bios, et ont trouvé qu'il y en avait dans aucun des vins bios, et des traces dans 14 des 16 vins non-bios.
Les auteurs disent même qu'ils ont été "surpris de trouver une telle différence".

Sauf que, sauf erreur de ma part, ils ont choisi 250 pesticide qui sont interdits en agriculture biologique, et n'ont pas testé des pesticides autorisés en agriculture biologique... Du coup, waouh, je suis très surpris par le résultat... 🙄

(pour info, la liste des pesticides autorisés en agriculture biologique : agencebio.org/sites/default/…
À comparer à la liste des pesticides qu'ils ont testé disponible dans l'onglet "tables": gavinpublishers.com/articles/Resea…)

Ensuite, ils ont fait tester aux mêmes personnes 3 à 8 verres, contenant soit de l'eau avec des pesticides dilués aux mêmes concentrations que dans le vin, soit de l'eau pure (1 à 3 verres d'eau pure dans le lot).

Il faut noter que ces concentrations sont extrêmement faibles, dans l'article on nous dit que dans 1 mL, on a une concentration 50 000 fois inférieure à la limite règlementaire. Autrement dit, même en buvant la bouteille, vous êtes à 66 fois moins que dose limite autorisée.

Ensuite ça devient compliqué, on nous dit qu'il y a eu 195 tests, et que dans ces 195 tests, il y en a eu 147 où les gens ont dit déceler une différence entre pesticide et eau pure. Puis parmi ces 147 tests, les gens ont correctement différencié tous les verres dans 58% des cas.

Du coup, la question qu'il faut se poser c'est : "est-ce que 58% des cas c'est beaucoup ou pas ?"
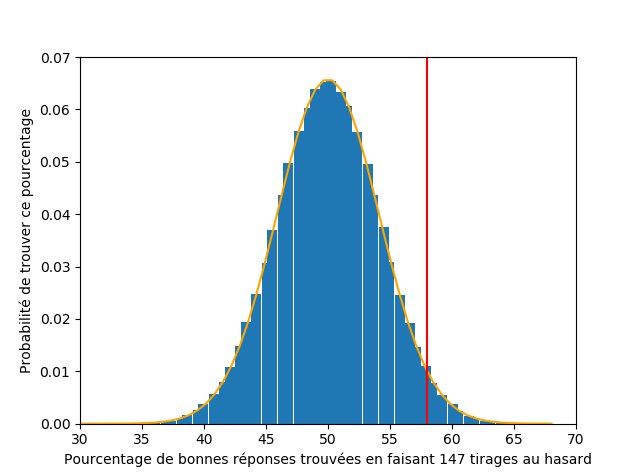
Et pour le savoir, il faut comparer avec les résultats qu'on obtiendrait au hasard.

Comment on fait ça ?
Eh bien, comme on sait qu'il y a 143 expériences, on va faire 143 tirages aléatoires (où le résultat peut être 0 ou 1 avec la même probabilité), regarder la moyenne, et répéter plein de fois ce tirage pour voir qu'elles sont les valeurs qu'on peut obtenir.

Sur cette courbe, vous avez la distribution des moyennes (exprimées en %) que j'ai obtenues en faisant un millions de fois un set de 143 tirages aléatoires.

(si vous reconnaissez une Gaussienne, c'est normal, en fait il y a une formule théorique pour calculer cette courbe, mais j'ai fait une simulation juste pour montrer le principe)

(en gros, ce que je cherche à savoir, c'est : "si je fais un série de 143 tests à la suite en répondant au hasard, quel va être mon taux de bonnes réponses")

Ce qu'on voit, c'est que la courbe est centrée sur 50%, c'est normal, si je réponds au hasard, en moyenne je vais trouver la bonne réponse réponse dans 50% des cas. Mais on voit que je peux aussi avoir de la chance et avoir + de 50% de bonnes réponses sur mes 143 tests au hasard.

Du coup, ce qu'il faut regarder c'est : combien de fois, en répondant complètement au hasard sur 143 tests, je trouve plus de 58% de bonnes réponses. Et on voit que c'est "pas souvent" (la barre rouge indique 58% sur la courbe) : dans moins de 2% des cas.

Du coup, ça voudrait a priori dire que la détection des pesticides n'est pas due au hasard, puisque les gens ont détecté les pesticides dans 58% des 143 tests (et que si c’était du hasard pur, ils n'auraient que 2% de chances d'avoir ce résultat).

(là je me demande si j'ai perdu tout le monde, et en plus je me rends compte que j'ai écrit "143" partout alors qu'en fait c'était "147" 😅)

MAIS, car il y a un "mais", c'est oublier un peu vite qu'en réalité il n'y avait pas 147 tests, mais bien 195. Et sur ces 195, il y en a donc 48 où les gens n'ont pas différencié pesticide très très dilué et eau pure.

Au total, on a donc, 58% de 147 = 85 tests où les gens ont bien différencié, et 42% de 147 + 48 = 62 + 48 = 110 tests où les gens n'ont pas différencié.
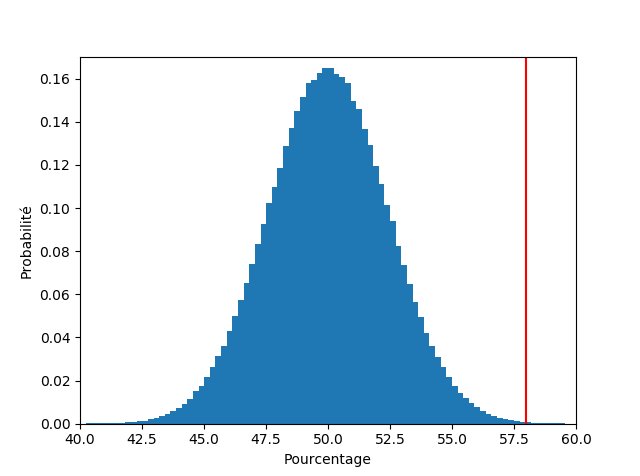
Du coup, si on prend tous les tests, les gens ont trouvé la bonne réponse dans seulement 44% des cas...

Et 44%, c'est bien moins bon que le hasard, même pas besoin de faire des calculs pour s'en rendre compte...
Donc ça vient un peu plomber le résultat de 58% qui avait pourtant l'air solide...

(ah, et je me rends compte qu'en fait c'était pas "147 cas sur 195 où les gens ont différencié pesticide et eau pure", mais "147 cas sur 195 où les gens ont dit voir une différence notable entre les deux vins", mais du coup c'est pire : pourquoi avoir éliminé les 48 autres cas ?)

(et pourquoi ne pas dire dans combien de ces 48 cas où les gens ont dit "on voit pas de différence", il y en avait où en fait il y avait vraiment une différence ?)

Enfin, on nous dit que dans 57% des cas, les gens ont identifié juste au goût quel était le vin qui contenait des pesticides. Sauf que c'est la même remarque que pour les 58% de gens qui différencient eau pure et pesticides dilués...

Ces 57% sont pris parmi les 147 cas où les gens ont annoncé avoir décelé une différence au goût, donc ça veut dire qu'en réalité, il y a moins de 50% des 195 cas où les gens ont différencié vin bio et non bio juste au goût...

Et comme le fait remarquer très justement @Timeo_Danaos, en plus, il n'y a pas d'expérience de contrôle. C'est-à-dire une expérience où on rajouterait des pesticides dilués dans le vin bio, et où on le ferait tester aux gens...

Bref, je suis : pas convaincu.
(et en plus, comme de toute façon je ne bois pas de vin, ça me fait une belle jambe 😇)

(et si vous voulez d'autres exemples de tests de vins en aveugle qui donnent des résultats surprenants sur l'incapacité des gens à différencier les vins, vous en avez quelques uns ici : en.wikipedia.org/wiki/Blind_win…)

ARGH ! Erratum !
Je suis un boulet et il y avait une erreur dans mon code, voilà la vraie courbe qui représente en y la probabilité de trouver x% de bonnes réponses en faisant 147 tirages au hasard.

(cette fois j'ai tracé en bleu le résultat de la simulation où j'ai fait un millions de fois 147 tirages aléatoires, et en jaune le résultat théorique attendu via le théorème centrale-limite, histoire de vérifier que je ne m'étais pas encore trompé !)

(et notez que le calcul avec la valeur de 2% était correct, il n'y a que la courbe qui était fausse, d'ailleurs, vous auriez pu me le signaler, c'était vraiment clair qu'il n'y avait pas 2% de l'aire sous la courbe au delà de la barre verticale rouge 😏)

On me fait remarquer (merci @HumainCurieux) que j'ai sans doute fait une hypothèse un peu forte en considérant que les 48 tests qui n'ont pas été pris en compte étaient tous négatifs. Et je suis d'accord avec ça. En réalité on ignore les résultats de ces tests.

Du coup, on ne peut pas savoir quelle est la vraie proportion de tests réussis, et de tests échoués (il faudrait savoir sur les 48 tests non pris en compte combien ont été positifs), et rien dans l'article ne nous permet de la calculer.

En revanche, il y a un chiffre que je n'ai pas discuté, mais qui peut être intéressant à regarder aussi, dans l'article on nous dit que sur les 147 tests conservés, il y en a 85% où les gens ont détecté au moins un verre contenant des pesticides dilués.

Et 85% ça a l'air beaucoup donc on pourrait se dire que c'est très fiable. Sauf qu'il faut encore se demander "combien j'aurais en faisant complètement au hasard". Je rappelle qu'il y a entre 3 et 8 verres, dont entre 1 et 3 contiennent de l'eau, et le reste des pesticides dilués

Du coup prenons un exemple, si j'ai 3 verres dont 1 qui contient de l'eau, et que je répons complètement au hasard, quelle est la probabilité que j'identifie correctement au moins un verre qui contient des pesticides dilués ?

On peut oublier le verre qui contient de l'eau, parce qu'on ne s'intéresse qu'à l'identification de ceux qui contiennent des pesticides. La probabilité qu'on se trompe pour les deux est de : 0,5x0,5 = 25%. Donc la probabilité qu'on en ait au moins un de bon est déjà de 75%.

Si maintenant je prends le cas où j'ai 8 verres, dont 3 qui contiennent de l'eau, la probabilité que je me trompe sur les 5 verres qui contiennent des pesticides est de : 0,5^5 = 3%. J'ai donc 97% de chances d'en identifier correctement au moins un, en répondant juste au hasard !

Étant donné que l'article ne donne pas le détail des répartitions de verre, on ne peut pas calculer la probabilité exacte qu'on aurait d'identifier correctement au moins un qui contient des pesticides en répondant au hasard, mais c'est entre 75% et 97%.

Du coup, le résultat de 85% de cas où il y a au moins une identification réussie ne me parait pas très impressionnant...