Thread by @math3ma

I’m happy to share a new paper with @MStoudenmire and John Terilla: arxiv.org/abs/1910.07425 We share a tensor network generative model, a deterministic training algo & estimate generalization error, all with the clarity of linear algebra. Now on the blog! math3ma.com/blog/modeling-…

@MStoudenmire I’ll explain some of the ideas here, sticking to a "lite" version. (Check out the paper for the full version!)

If you’ve been following the posts on Math3ma for the past 6-or-so months, you’ll be delighted to know the content is all related. But more on that later…

@MStoudenmire Alright, before jumping in, let’s warm up with a question:

@MStoudenmire Example? Take bitstrings—sequences of 0s and 1s, all of length 16, say. There are 65,536 of them but suppose we only have a fraction, drawn from some probability distribution. We may/may not know what it is, but perhaps we’d like to use the samples to infer it and sample from it.

@MStoudenmire As another example, suppose our data points are meaningful sentences—sequences of words. Natural language has a probability distribution on it (e.g. “cute little dog” has higher probability of being spoken than “tomato rickety blue”), though we don’t have access to it.

@MStoudenmire But we might like to use the data we *do* have to estimate the probability distribution on language with the goal of generating new, plausible text. (Hello language models!) quantamagazine.org/machines-beat-…

@MStoudenmire These examples, I hope, help put the paper in context. We’re interested modeling probability distributions given samples from some dataset.

More specifically, we’re interested in modeling probability distributions on *sequences*—strings of symbols from some finite alphabet.

@MStoudenmire So the goal is two-fold:

1. Find a model that can *infer* a probability distribution if you show it a few examples.

2. Understand the theory well enough to *predict* how good the model will perform based the number of examples used.

@MStoudenmire And that’s what we do! We present a theoretical model and share a training algorithm, and also include a roadmap for theoretical analysis, with experimental results to illustrate.

@MStoudenmire Specifically, we work with the even-parity dataset: We start with some examples of even parity bitstrings of length 16 (a bitstring has ‘even parity’ if it contains an even number of 1s), and then aim to predict model’s performance based on the fraction of examples used.

@MStoudenmire I won’t get into details (they’re in the paper!) but I will share a few words about the model since I’ve blogged/tweeted about it before.

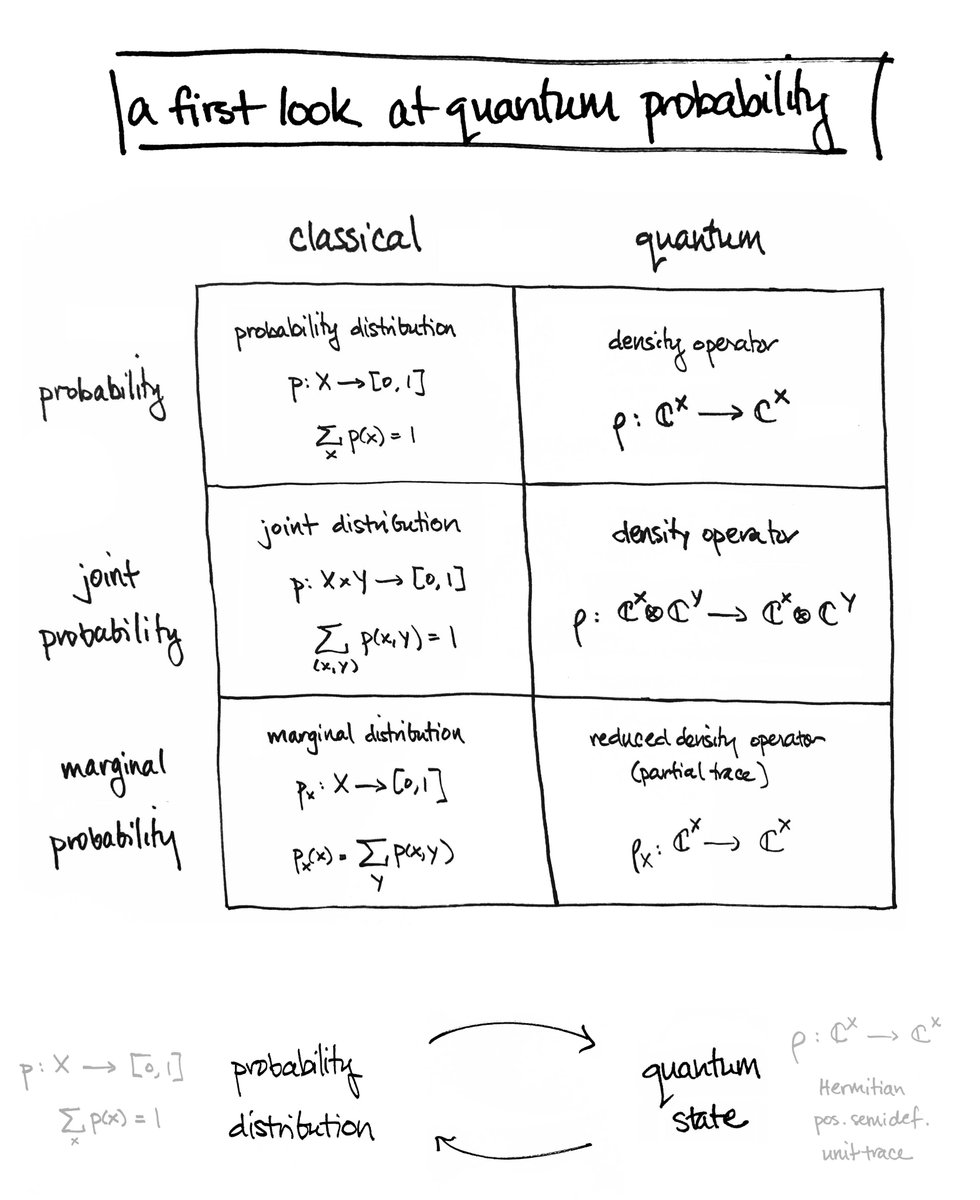
It’s very simple: We model probability distributions by density operators, a special kind of linear transformation.

@MStoudenmire I’ve written about this idea before. Check out “A First Look at Quantum Probability” for all the details: how to get a density operator from a probability distribution, and why this is a useful thing to do! math3ma.com/blog/a-first-l…

@MStoudenmire Or for a bite-sized intro to these ideas on quantum probability theory, check out this old thread:

https://twitter.com/math3ma/status/1153854415742234624

@MStoudenmire In any case, the main idea is very simple and worth sharing again:

Given an empirical probability distribution on a training set of sequences, we define a unit vector which is essentially the sum of the samples weighted by the *square roots* of their probabilities.

@MStoudenmire By passing from a probability distribution to a unit vector, we’ve moved from the world of probability theory to the world of linear algebra.

And since the coordinates of the vector are *square roots* of probabilities, we are in the realm of “2-norm probability.”

@MStoudenmire “2-norm probability” usually goes by the name of quantum probability—and a density operator (obtained by orthogonal projection onto that unit vector) is called a quantum state—but it's really just another way to think about probability.

It's just linear algebra!

@MStoudenmire Alright, so what do we do with that unit vector? (i.e. the sum of training samples, weighted by the square roots of their probabilities.)

We tweak it to get a *new* vector.

This is all happening in a tensor product of Hilbert spaces, so there are nice tensor network diagrams:

@MStoudenmire The new vector is a special kind called a matrix product state (MPS).

MPS are nice bc far fewer parameters are needed to describe them than a generic vector in a tensor product. This is especially useful if you're working in ultra-large-dimensional spaces. MPS are efficient!

@MStoudenmire Anyways, the punchline: We reach our goal! The probability distribution defined by (the squares of the entries of) the MPS is very close to the *true* distribution on bitstrings that we wanted to infer from the dataset.

@MStoudenmire Even better, we can estimate the model's performance, based on the fraction of training examples used:

🔶 = experimental average
🔷 = theoretical prediction

The results are produced using the @ITensorLib library, itensor.org; details are in Section 6 of the paper.

@MStoudenmire @ITensorLib Section 4 presents the training algorithm to get the MPS. It consists of successive applications of SVD on reduced density operators. The reason why we do this—and why an MPS is a natural choice of model—is inside this thread on quantum probability theory:

https://twitter.com/math3ma/status/1153854415742234624d

@MStoudenmire @ITensorLib In short, the success boils down to ONE crucial fact:

✨Eigenvectors of the reduced densities of pure, entangled quantum states contain conditional probabilistic information about your data.✨

I won’t unwind this here. It’s all laid out on Math3ma:
math3ma.com/blog/a-first-l…

@MStoudenmire @ITensorLib So we capitalize on this. Each tensor—blue node—in our MPS model *is* an array of eigenvectors of some reduced density operator obtained from that original vector (the sum of the training samples, weighted by the square roots of their probabilities).

@MStoudenmire @ITensorLib Result? The model *knows* what "words" go together to form "meaningful sentences" just based on the statistics of the training data. And it's all just simple linear algebra, so we understand when/why/how the model succeeds or fails, given the number of training examples.

@MStoudenmire @ITensorLib Mission accomplished!

@MStoudenmire @ITensorLib By the way, the heart of the algorithm is really very simple, but it goes by a sophisticated name in physics literature: the "density matrix renormalization group" (DMRG) procedure, introduced in 1992 by physicist Steven White.

journals.aps.org/prl/abstract/1…

@MStoudenmire @ITensorLib DMRG is usually used to find a particular eigenvector of a linear operator (the Hamiltonian of a quantum many-body system), but we instead apply it to our special vector: the sum of the training examples.

@MStoudenmire @ITensorLib In short, the results are clear and interpretable since it's all just linear algebra, so we're able to give an "under the hood" analysis of the theory in Section 5, which is what allows us to make those theoretical predictions about the model's ability to generalize.

@MStoudenmire @ITensorLib (There's a bit of combinatorics involved, and we end up representing matrices as bipartite graphs for bookkeeping purposes. This is what inspired the article ‘Viewing Matrices and Probability as Graphs’ from earlier this year.)

https://twitter.com/math3ma/status/1103328155429949440

@MStoudenmire @ITensorLib There's lots more to say, but I'll stop here.

I might share a deeper look into the mathematics later in the future. In the mean time, feel free to dive in! arxiv.org/abs/1910.07425

</thread>