🆃🅴🅾🆁🅴🅼🅰 del ladrillo (aleatorio) en la pared.
Si en lugar de poner los ladrillos como en la pared de The Wall permitimos que vayan acostados o parados (como en la otra foto). ¿Cuántas formas hay de hacer la pared?
#TeRegaloUnTeorema
(sigue)

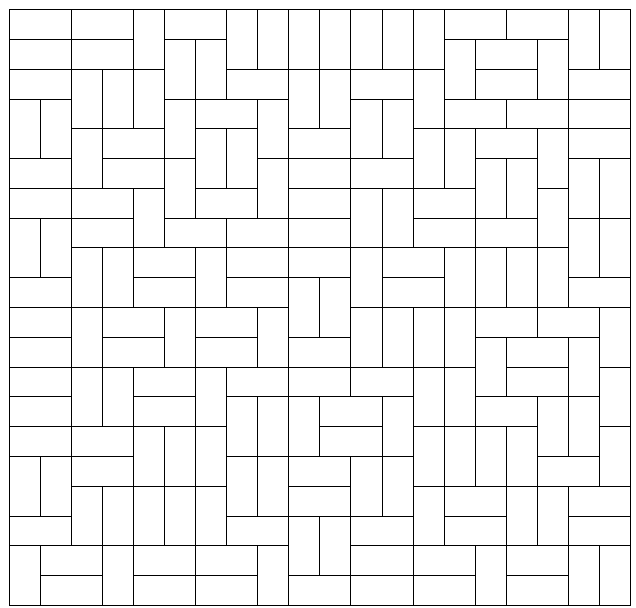
La demostración no es dificil y pueden encontrarla en arxiv.org/pdf/math/03103…