Thread by @Steve_J_

Ces derniers temps je râle sur le fait que les non-statisticiens ne parlent pas assez de marges d'erreur quand ils cherchent à évaluer la qualité d'un sondage.
Du coup un petit thread sur comment évaluer grossièrement la qualité des résultats d'un sondage par quota.

Certains instituts mettent en avant cette table de précision, comme ici l'@IfopOpinion dans sa dernière publication sur la popularité du PM.
ifop.com/media/poll/394…

Cette table repose sur des hypothèses un peu lourdes sur la constitution de l'échantillon et les comportements de réponses.

Je n'entre pas trop dans les détails, il y aurait des choses à dire (idéalement il serait bon d'avoir une idée des taux de réponse - nombre de répondants/personnes contactées - pour savoir si ces derniers sont particuliers). Pour une première approche c'est déjà un bon outil.

On se rend compte que la précision d'un chiffre dépend du nombre de répondants ET des proportions estimées (je simplifie).
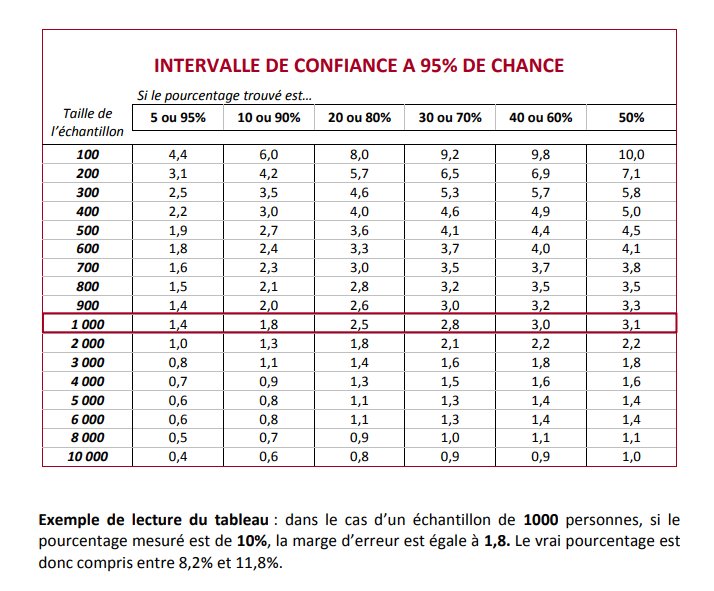
Si sur un échantillon de 1000 personnes on trouve 50 % de sympathisants du PM, la marge d'erreur sera de +/-3,1pt, si on en trouve 80 % elle sera de +/-1,8pt

Cela permet de se faire facilement une idée de la qualité des chiffres clefs de l'étude, calculés sur l'ensemble de la population d'intérêt.
Ici on nous dit que 53 % des français font confiance au Premier Ministre, la marge d'erreur est d'environ +/3pt...

...la vraie valeur se trouve sans doute entre 50 et 56 %.
Je dis "sans doute" mais on pourrait sans trop de casse remplacer par "La vraie valeur à 95 % de chances d'être dans cet intervalle (dit "intervalle de confiance").

Sauf que, cette première approche, ne fonctionne pas sur les sous-population.
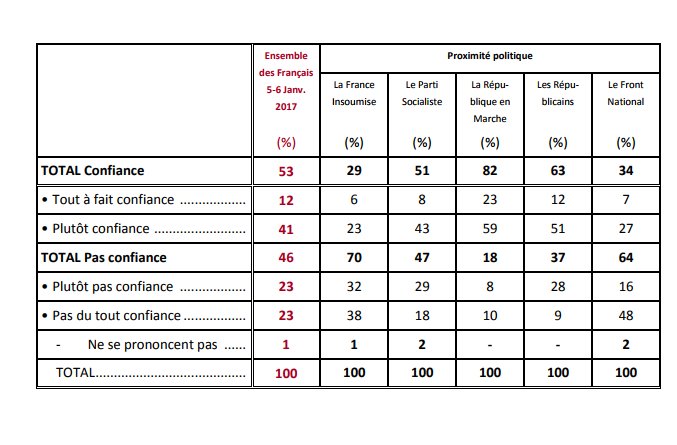
Or la plupart des résultats de sondages repose sur un croisement entre une variable étudiée et un sous groupe d'intérêt.

Par exemple on apprend ici que 29 % des gens qui se sentent proches de la FI apprécient le PM.
=>Comment évaluer ce chiffre qui n'est calculé qu'avec une petite fraction de l'échantillon total (les répondants qui se sentent proche de la FI) ?

Si on connaissait le nombre de répondants proches de la FI on pourrait envisager d'utiliser le tableau de précision...mais l'info n'est pas fournie.

On sait 2-3 trucs sur la constitution de l'échantillon, il repose sur la méthode des quotas qui cherche à avoir les mêmes proportions de certaines catégorie dans l'échantillon et dans la population.

Les données utilisées ne sont pas fournies mais il s'agit de variables trouvables sur des sites d'instituts statistiques.
Par exemple, le calcul est un peu pénible à faire, mais avec ces tableau on trouve que 24 % de la population français a +de 65 ans.
insee.fr/fr/statistique…

=>Le sous-échantillon des plus de 65 ans doit rassembler environ 240 répondants
=>Quand on lit que 69 % des 65 ans et + approuvent l'action du PM la marge d'erreur est d'environ +/6 points : le "vrai" chiffre est sous doute entre 63 et 75 %

Je reviens à mon chiffre portant sur les partisans de la FI et...c'est compliqué.
=>la variable "proximité politique" n'est pas dans les quotas...pas sûr que les proportions soient les mêmes entre l'échantillon et la population
=>quelle est la part des FI dans la pop ?

=>On peut/est obligés de se rajouter l'hypothèse que la part des sympathisants FI ne doit pas être radicalement différente entre l'échantillon et la population.
=>Dans un sondage Harris je trouve 10 % de sympathisants FI/PCF...c'est mieux que rien
harris-interactive.fr/wp-content/upl…

Cela ne me plait pas beaucoup mais, au doigt mouillé, faisons comme si 10 % de l'échantillon (environ 100 répondants) était composé de sympathisants FI.
Cela nous amène à estimer qu'entre 15 et 30 % des sympathisants FI apprécient le PM...

Voilà donc une façon, certes grossière et insatisfaisante, de se faire une idée de la qualité des chiffres d'un sondage par quotas.

Les quantitativistes de ma TL je suis curieux de savoir si vous procédez différement.