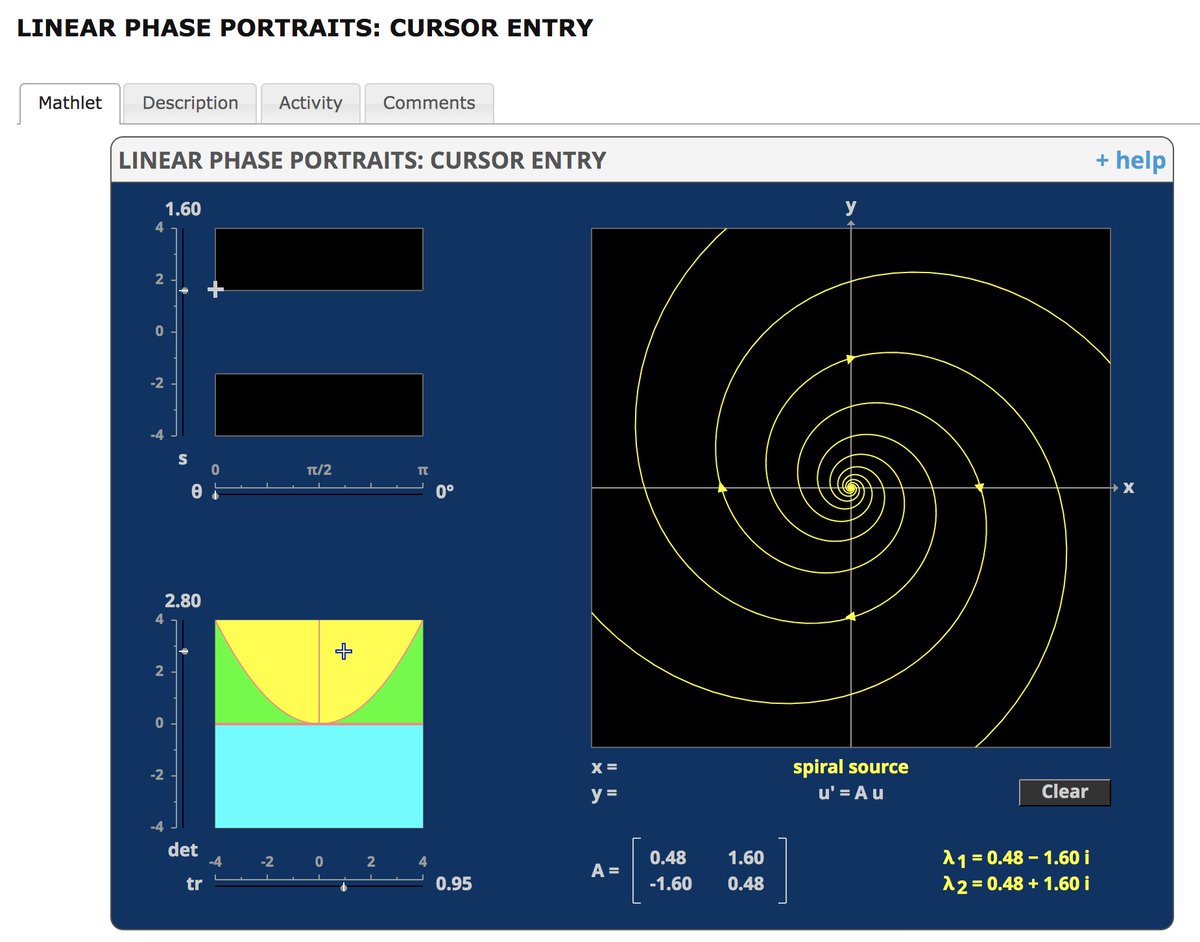
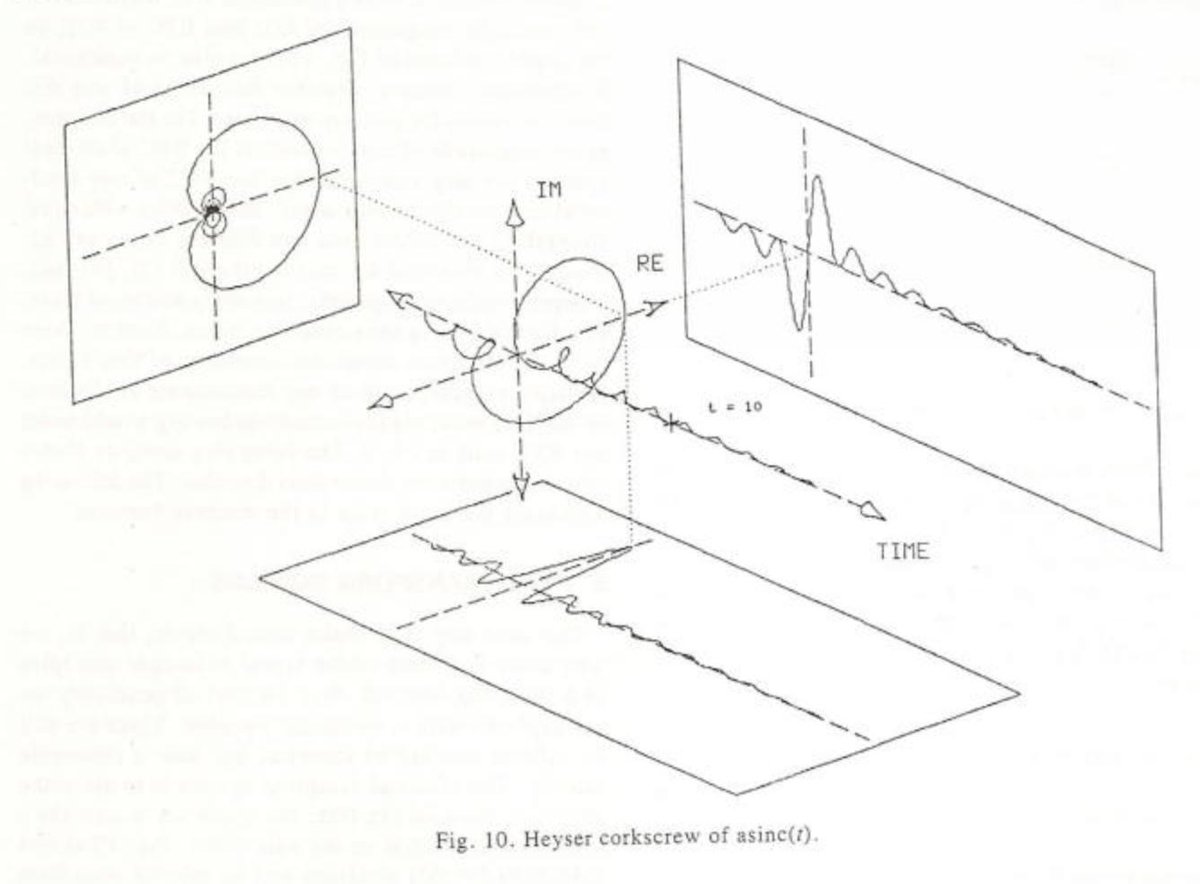
An interactive version by @rickyreusser here: rreusser.github.io/logistic-map/
Original paper introducing the idea here: pdfs.semanticscholar.org/752e/0468e5e2e…
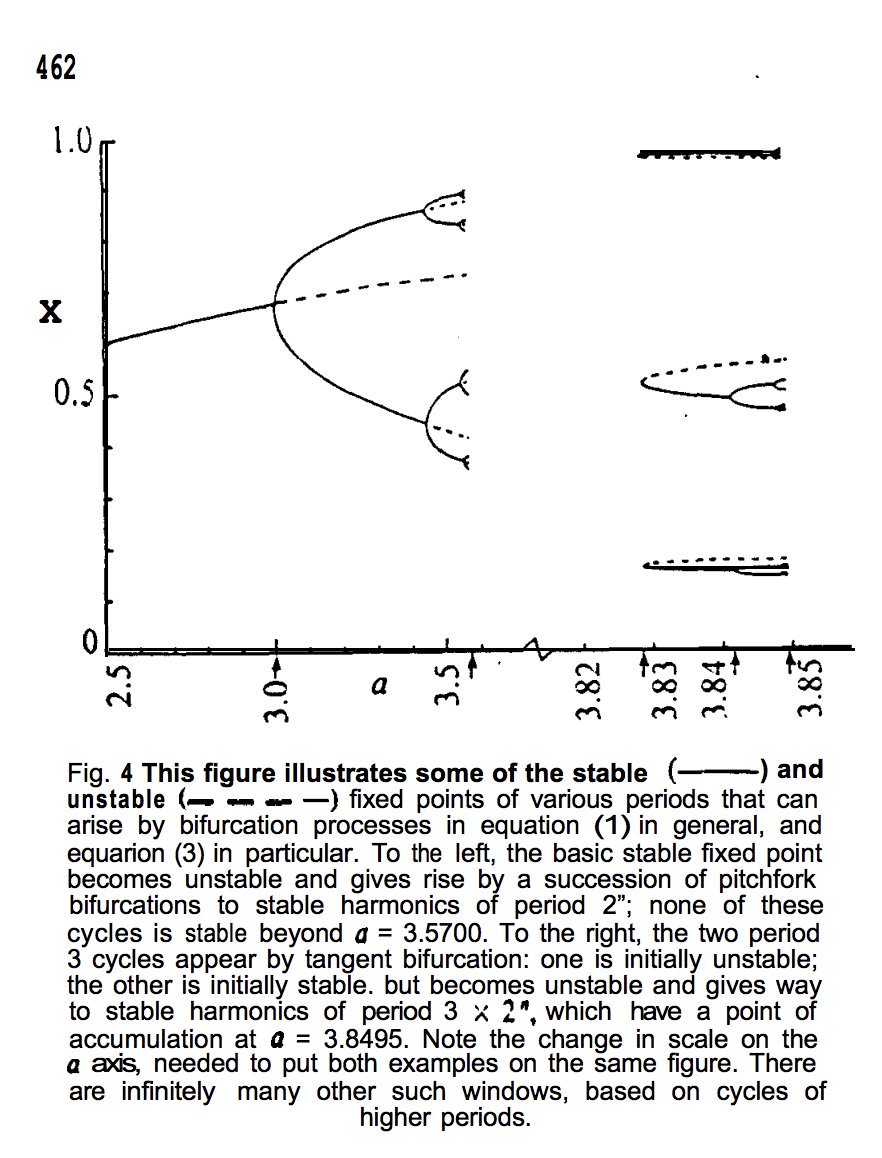
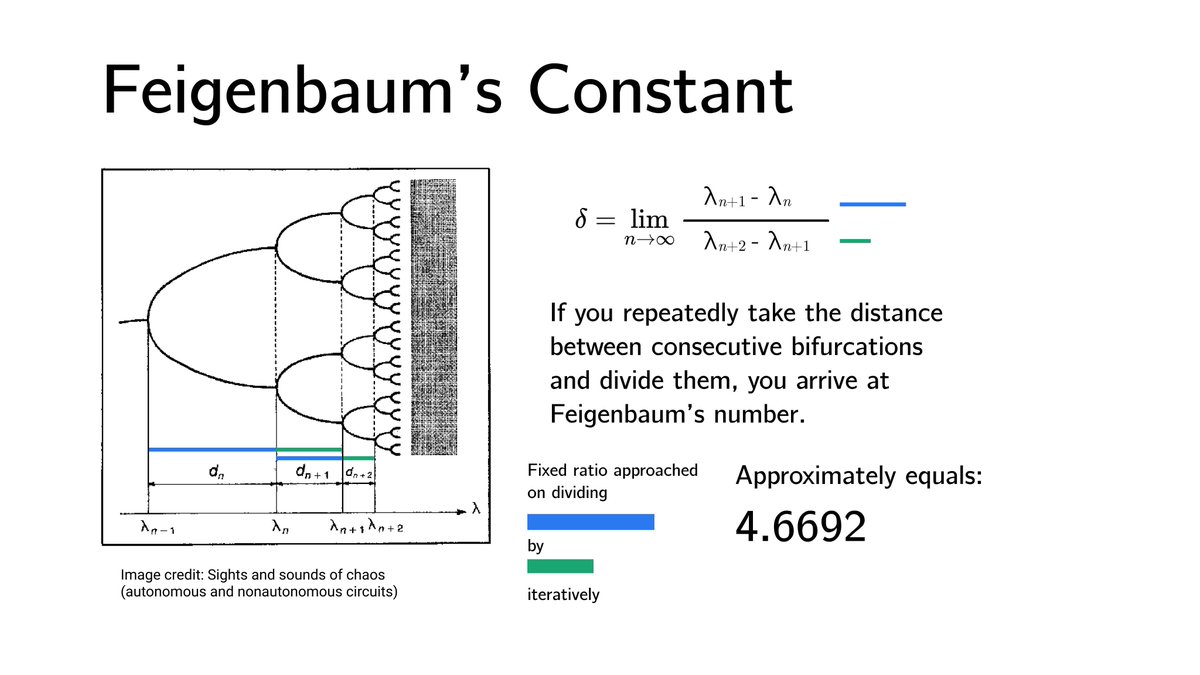
And here's @unconed's visualization of the same: acko.net/blog/how-to-fo…


I guess at this point it might be valid to say the logistic map is a leitmotif present inside the Mandelbrot.
His @ComplexTrees account is also well worth checking out!