Over the long term, 1 in 10 will be killed by that choice.
And be seen as a crusader against a crooked medicogovernmental conspiracy.
The internet is a good place to operate, because most lay people can't distinguish scientific reasoning from pseudoscience, and because ...


So statin-denial is the best way to kill low risk people.

Even the statin nitwits generally don't try to deny secondary prevention.
This is all primary prevention.
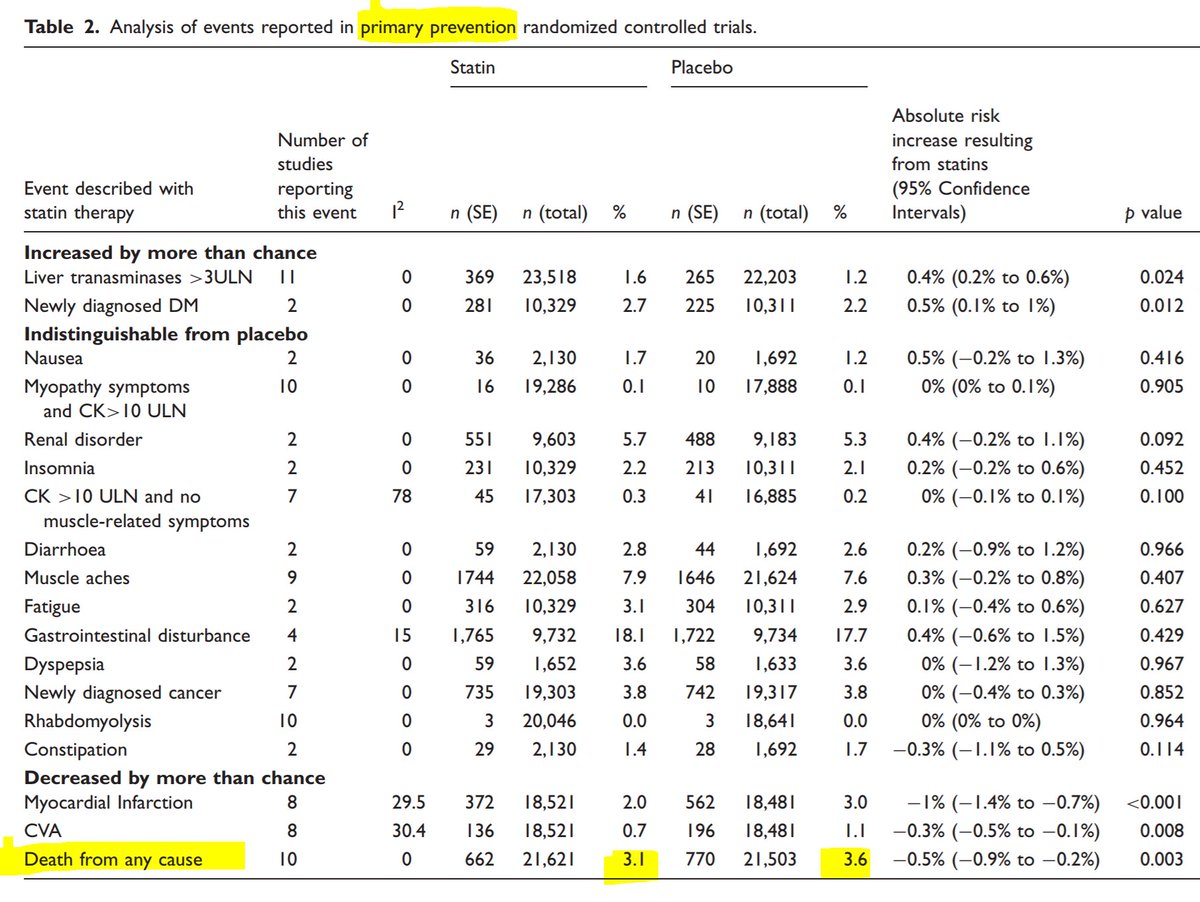
Try the Finegold meta-analysis of unwanted outcomes, including muscle pains, diabetes and death.
Only ~10% will live longer. [They live about 10 years longer on average.]
So if you get 1000 people to choose AGAINST statins, how many people will live shorter lives?
It is REALLY good for people to look at the data and demand answers like this.
Much better than reading hysterical hype.

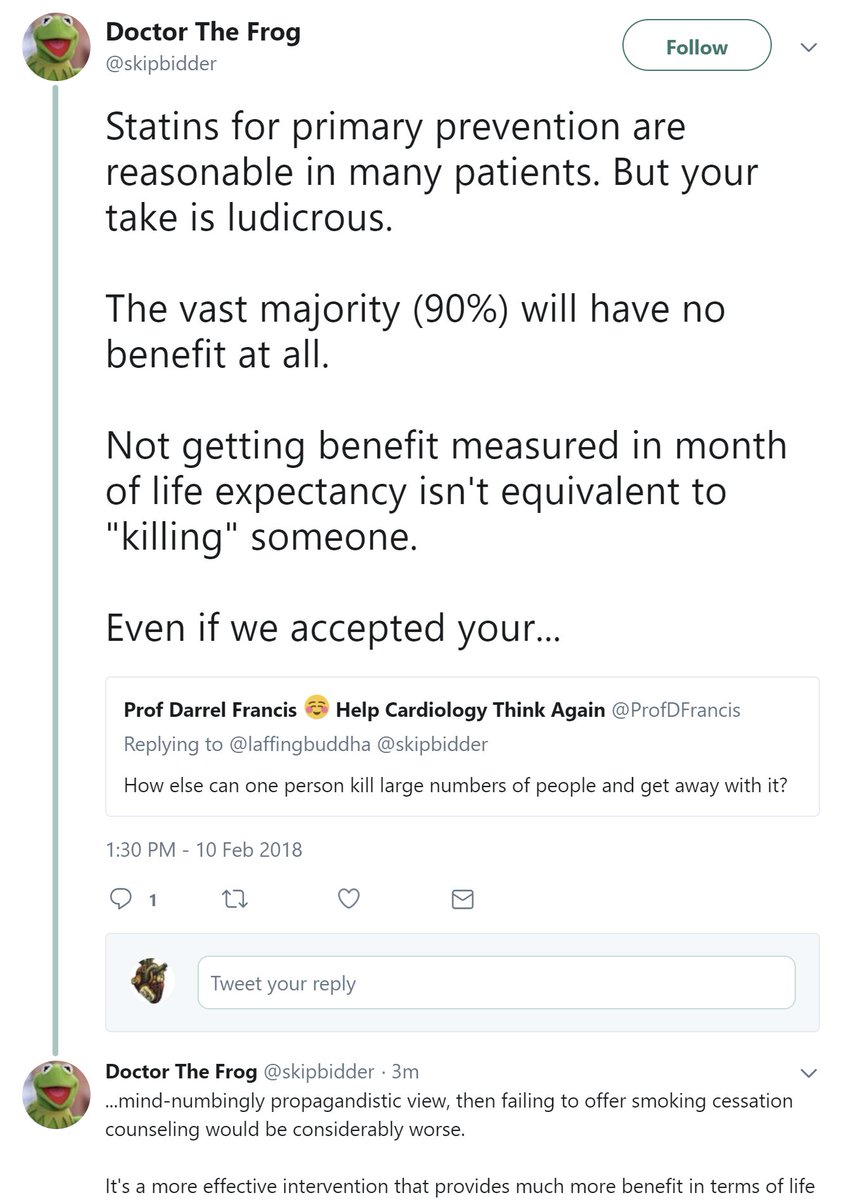
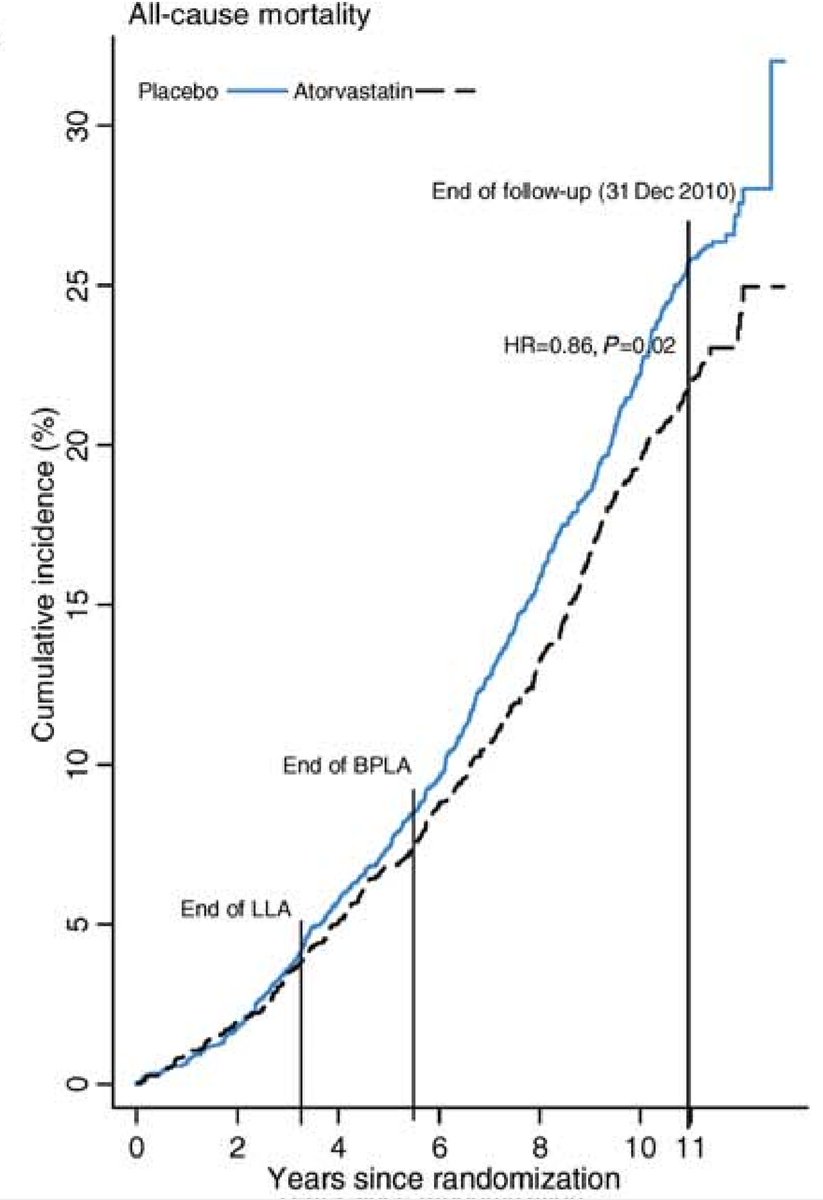
When the trial ended, 2.3% died in the placebo arm and 2.1% in the statin arm.
How many actual people died?
So how many deaths have you prevented?
At what time point have we been reading the numbers off?
How many were dead be in the Placebo and the Statin arms?
[Let's imagine we can have fractional people!]
The next year, I owed them more, $1200.
The year after, I owed them even more, $1430.
I shut my eyes. I hoped the debt would go way, or at least stop rising, by my act of not looking.
How much do I owe now?
"If a bank is charging you interest, even if there is nobody reading the bills, does it increase the debt?" #philosophy!
Starting a lifelong course of statins on the 1000 patients saves how many lives? What is the right answer?
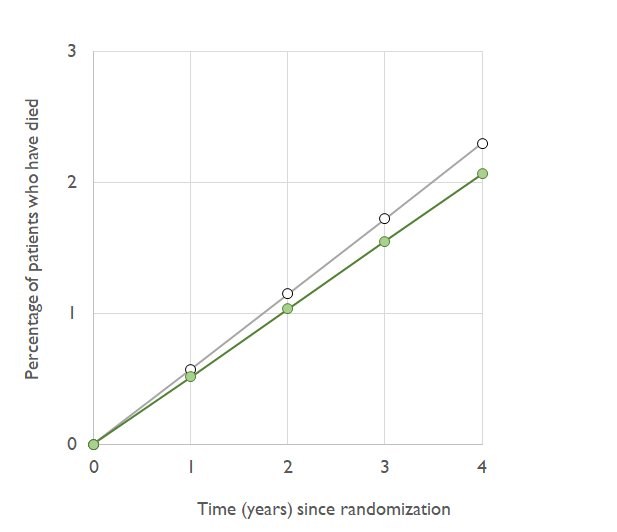
ASSUMING things went on the same trajectory, if you doubled the duration, how many do you think will have died at 8 years (twice as long as the point of 23 + 21 )
Within the duration of the trial, we can calculate it from real data.
After the trial ends, people are free to do whatever they want (i.e. statin or not) and we are not formally tracking their outcomes, so it is extrapolation.
If you don't, you are like most people. You realise you will die at some stage, but hopefully 10, 20, 30, 40 or more years in the future.
Have a look at ASCOT-LLA. In this trial patients had randomized statin for 3.3 years. But the trial reassessed survival at ~11y
At 0 years, 0/1000 life saved. That's terrible, but it's early days.
At 1 year, 0.5/1000 saved.
At 2 years, 1/1000
At 4 years, 2/1000
At 8 years, 4/1000
We could say "the only right duration is the duration of the trial", 4 years.
But wait!
CV risk rises 3-fold with every decade of life.
Suppose our trial has mean age 60 y.
A patient aged 70 y has 3x as much risk as the 2.3% and 2.1% of the average patient.
What is his mortality risk at 4 years, in the two arms?
Remember the mortality fell from 6.9% to 6.3%, and there were 1000 in each arm.
How much larger is the number of lives saved amongst 70 year olds (who have 3x the risk) than 60 year olds (who have average risk for the trial)
If we went older, or added diabetes, or smoking, we could get it even higher, to almost anything we want.
Assume the trials were otherwise similar.
Three-fold higher baseline risk, means what-fold ABSOLUTE lives saved?
And then each individual "end-user" of statins will be different, so the "ABSOLUTE" lives saved will differ.
Instead of the ABSOLUTE risk reductions in isolation, let's look at the numbers of deaths in each arm, side by side.
23:21 (at 4 y).
So adding the other time points:
11.5:10.5 (at 2y)
46:42 (at 8y)
And at 4 years lets try the 70 year olds
69:63
See anything?
What is the ratio between 42 and 46?
69 placebo and 63 statin deaths (based on being triple risk in both arms)
What is the ratio?
Statin divided by placebo
We call this the RISK RATIO.
What is the risk ratio for our trial?
Hint in next tweet if you want to do it without a calculator.
All ORBITA-HQ PhD'ers would be expect to get this right to within 5% of the right answer, in a snap.
21/23 is 1 minus 2/23.
2/23 is almost 2/20, or 1/10, which is 0.1. So FIRST APPROXIMATION IS 0.9
2/23 smaller than 2/20, by about 15%, because 23 is about 15% more than 20.
So don't deduct the "full" 0.1, deduct 15% less, i.e. add on 0.015.
SECOND APPROXIMATION is 0.915.
This is within 2 parts in a 1000 of truth:
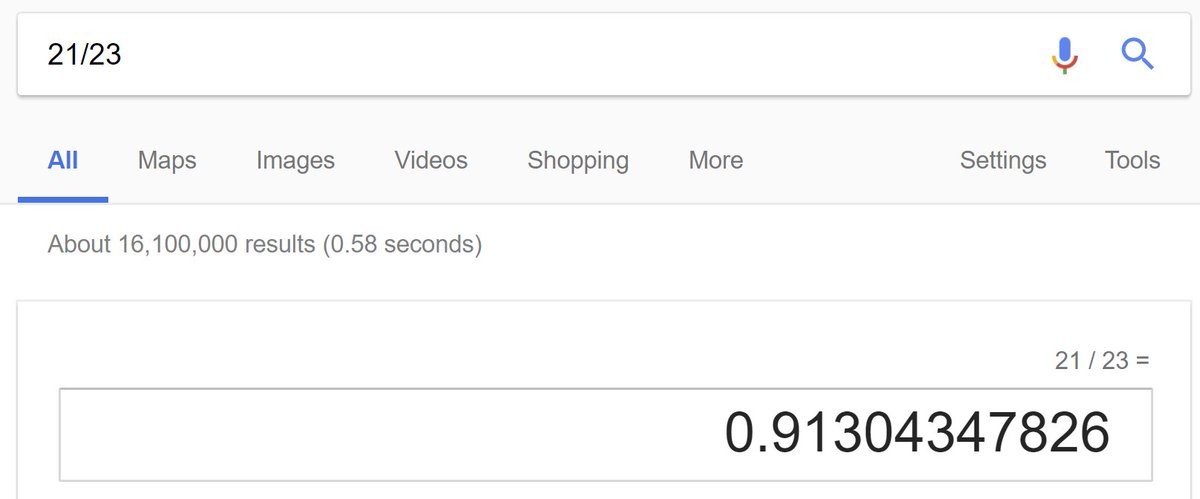
Inside it, any patient randomized to statin instead of placebo has only 0.91x as much chance of dying.
Young or old, diabetic or not, the ratio is roughly right.
I could use 0.91 as the principal number to talk about the trial. But it is a funny number. It has decimals, and lower is better. Two awkward features.
If you had a treatment that gave a 9% RELATIVE risk reduction, and your baseline risk over the trial duration was 10% in the control arm, what would it be in the active arm?
It is exactly the same as a "50% off" . That doesn't mean every item is $50 cheaper: only if they started at $100.
In a "50% off" sale how much is an originally $2 item reduced by?
And TO what price?

In trials, lay people can get confused, because BOTH the reductions AND the event rates are in "%". I am sorry for your frustration. We clinical scientists have got used to it.
One is "9% RELATIVE RISK REDUCTION"
The other is "0.2% ABSOLUTE RISK REDUCTION"
Both are correct.
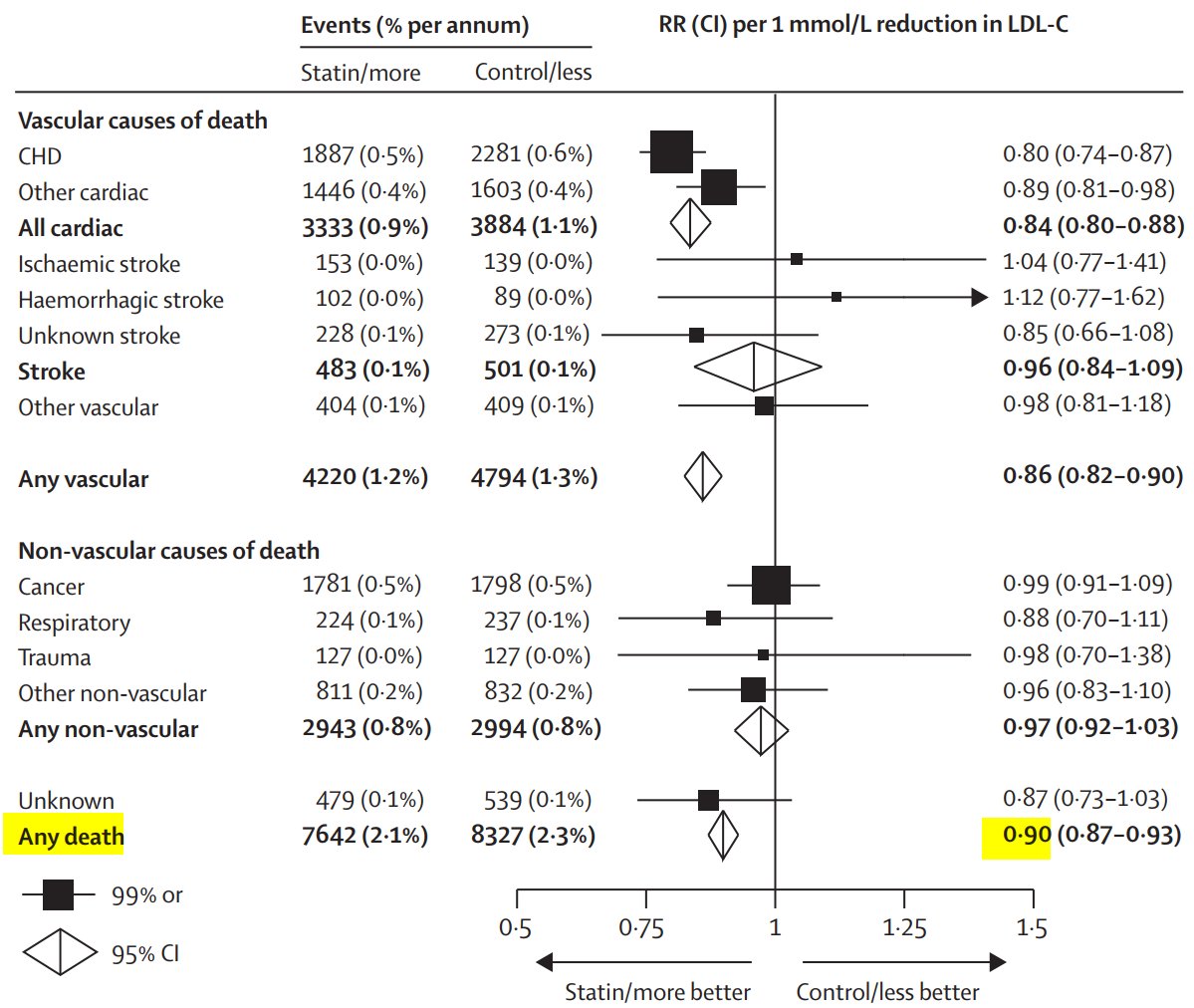
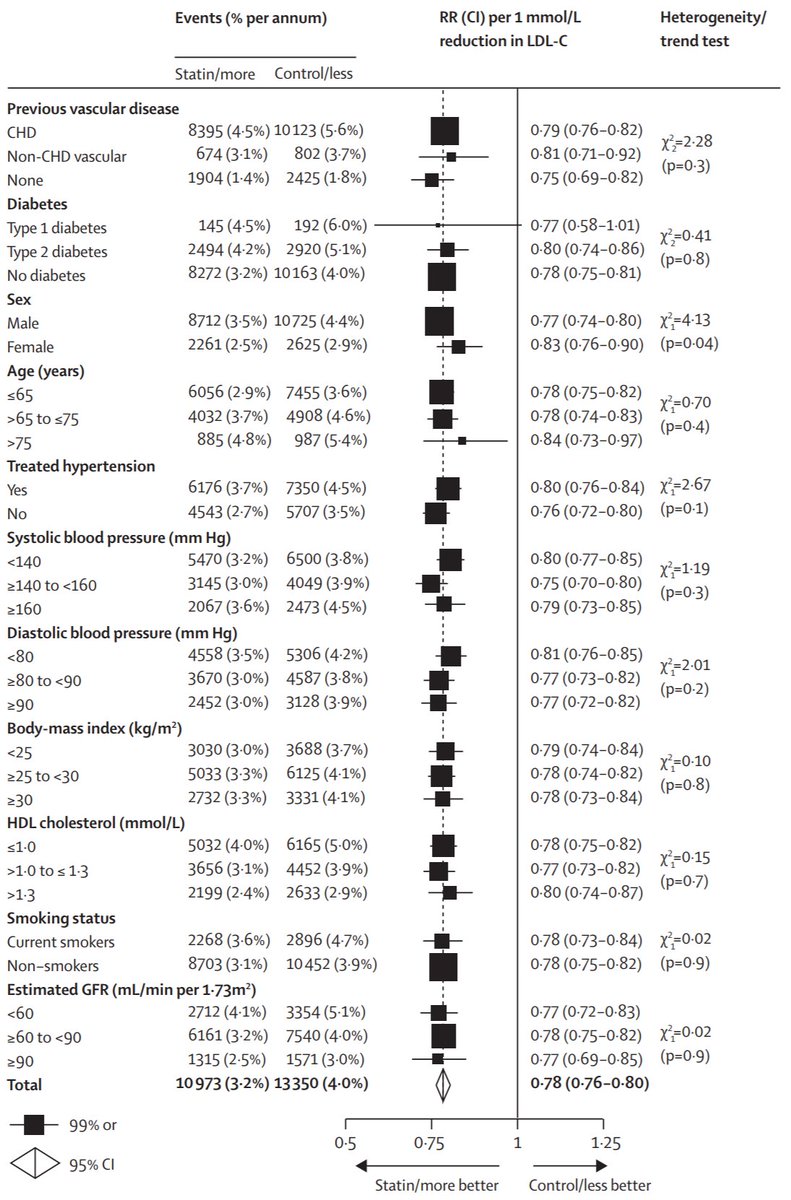
In fact CTT 2010 shows this splendid graph which I keep looking at in amazement and happiness.
Maybe I am wrong. Let's take a bit of a poll. Be honest.
Let's start at the top left corner.
What is the risk ratio for that, do you think?
Very clever statisticians of yesteryear worked out how much it varies. It basically depends on how many patients you have in your sample. If you have zillions, you are probably spot on and it won't vary.
But if you have only a few, it could vary a lot.
What you calculated was the POINT ESTIMATE (or most likely value), and it has a range of uncertainty around it: the 95% confidence interval.
Zoom out and we see it.
Why?
[When I give out something ~1.5 mM LDL reduction, I expect to get "one and a half" times as good effects as the CTT graph.]
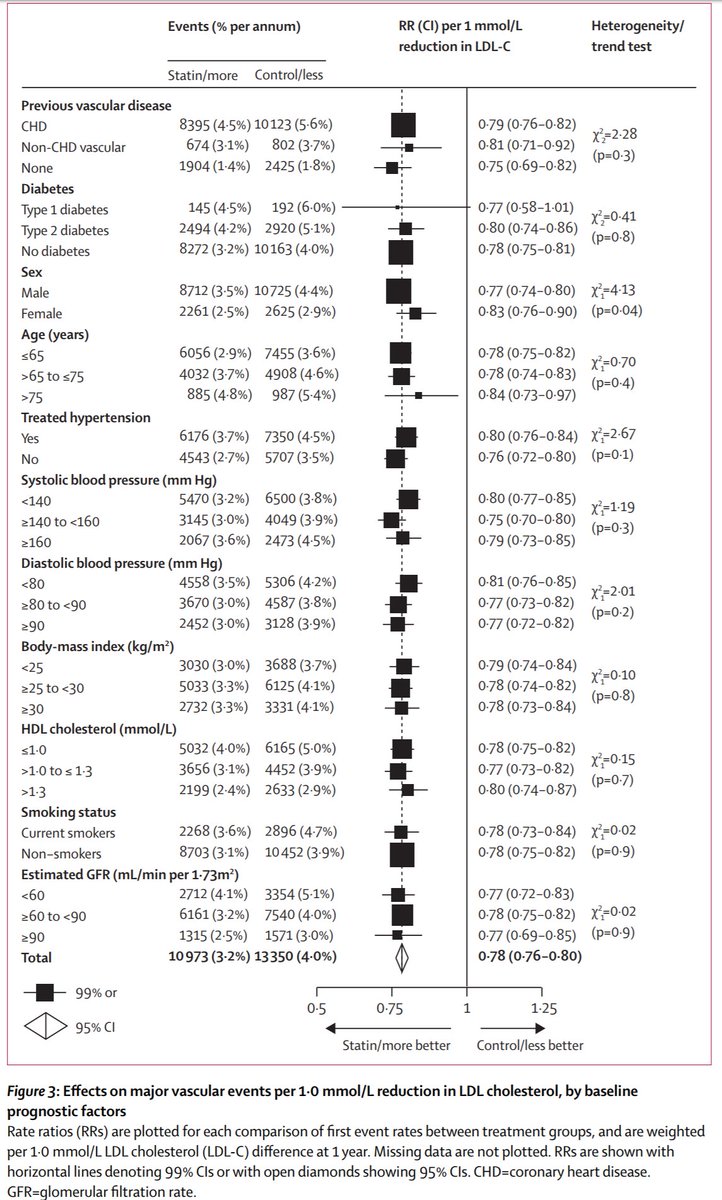
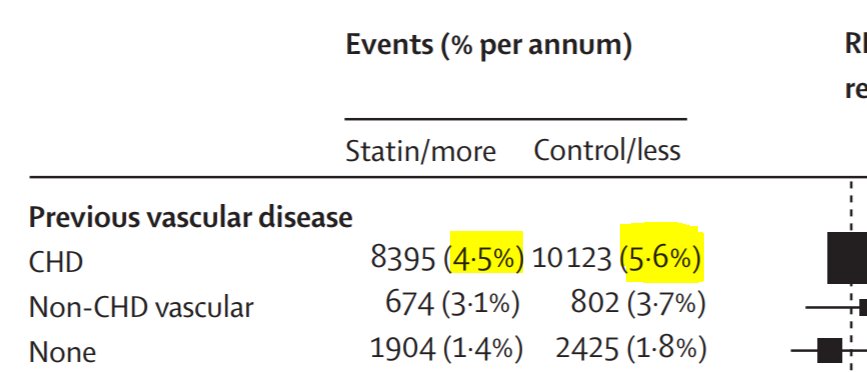
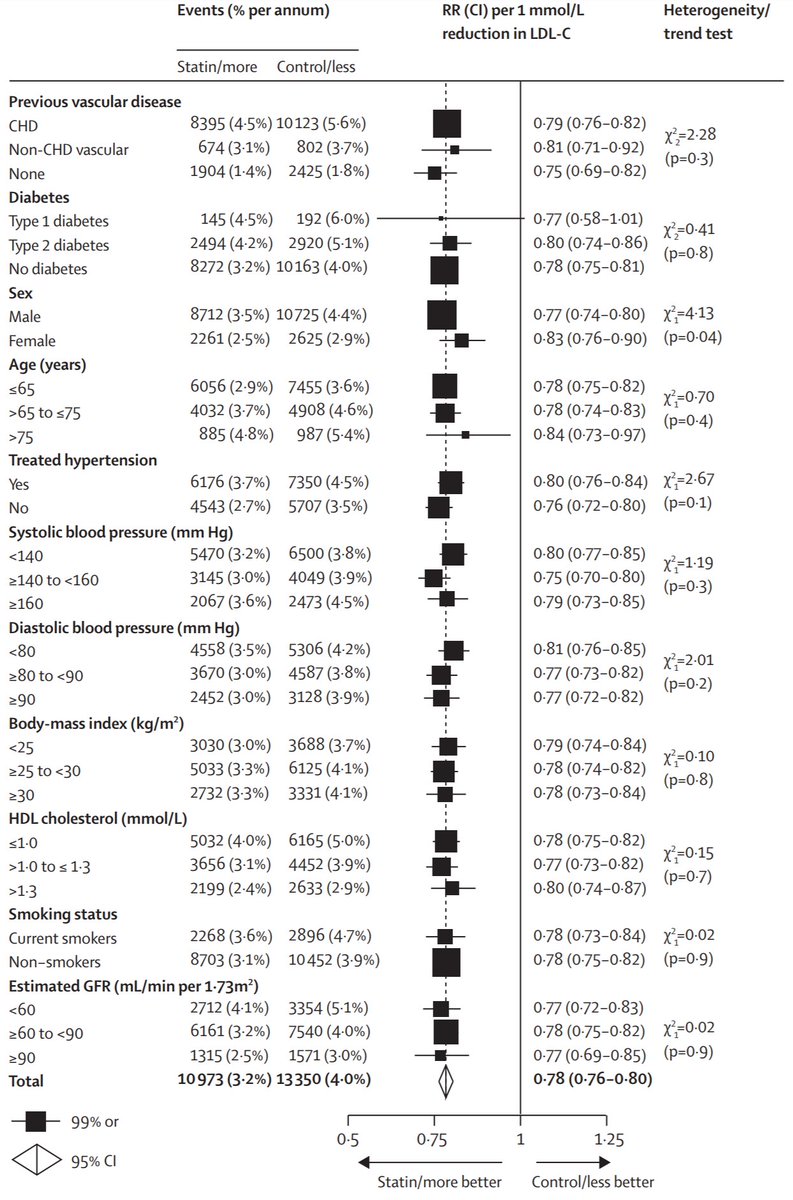
For people with a background of CHD, there is a 0.79 relative risk (also called a 21% RELATIVE risk reduction) if they take a statin of strength enough to lower LDL by 1 mM.
If you give atorva 40, ~1.5mM redn, what effect might you get?
Let's look at the third row.
People WITHOUT prior coronary heart disease.
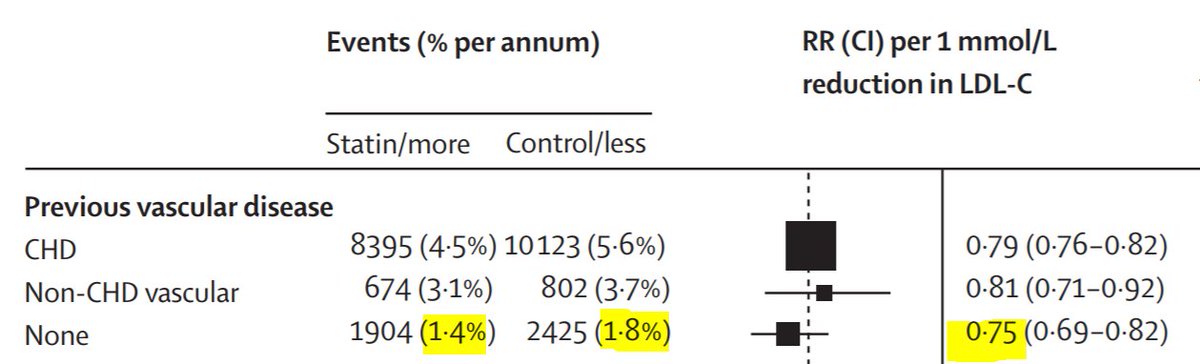
1. How does their risk (yellow row) compare with the risk of the people who HAVE coronary disease (top row)?
Third row. Risk falls from 1.8% to 1.4%, that's an absolute fall of 0.4%.
Top row is 5.6% down to 4.5%, that's an absolute fall of 1.1%.
How does the 3rd row (0.4%) compare against top row (1.1%)
But overall, we still prevent the same RELATIVE proportion of deaths:
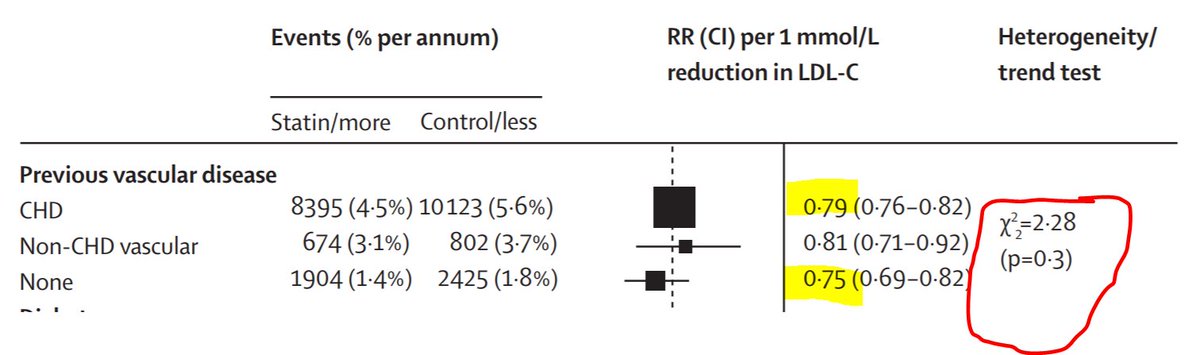
P>0.05: don't get excited.
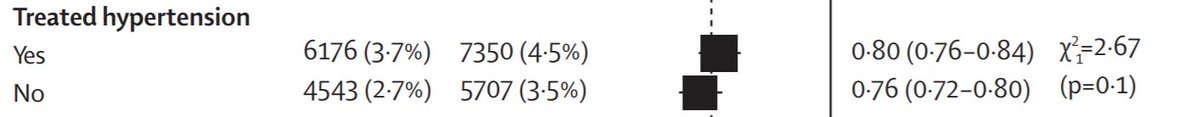
.
How about chubbiness?

It means THERE IS LESS TO KNOW. Thank god.
There is no subgroup that is convincingly different from its counterpart subgroup, in my eyes.
ABOUT 20% RELATIVE RISK REDUCTION for a 1 mM-strength statin (I tend to give atorva 40, which is 1.5mM typically, so a 30% RRR)
NO convincing difference between subgroups.
First from Tom Hyde, who is normally more sensible:
If he chooses no, he has A% mortality.
If he chooses yes, he has 0.9 x A% mortality.
If he WAS GOING to say yes, but you PERSUADE him to say no, his mortality is going from 0.9xA% to A%.
Scale factor is 1.0/0.9 = 1.11.
For a ~1.5mM-worth, it would be a little stronger.
As one ages, the non-cardiovascular forms of death may rise so that it may be weaker.
* stronger than 0.90 in early decades
* weaker than 0.90 in later decades
Thus I suggest to use 0.90 overall.
However you can use a continuously variable scale as used by Finegold.
openheart.bmj.com/content/3/1/e0…
I will give an hour
Regardless of LDL, regardless of BP, smoking status, age, etc.
They get approximately (say) 30% reduction in CV events (atorva 40).
Of course stop-smoking, control weight, reduce calories to improve diabtes, BP is important too.

"Are you interested in taking a tablet that will increase your life expectancy by ~1 year, delivered as follows.
90% chance of getting no increase in lifespan.
10% chance of getting an ~10 year increase."
Of course it is worth eating healthily and exercising
Strange but true. Fontana et al.
circ.ahajournals.org/content/early/…

We can stratify people a bit in risk, but however apparently good the stratification, the actual survival curves within the stratum start early and end late.
For any stratum, there is very large uncertainty in lifespan.

They are only similar in the direction of their effect on mortality, and the fact that you don't have to touch people to kill them: it all works through change in behaviour.
But a very small smoking habit might match anti-statin
Asked 13 hours ago, before the explanation of absolute versus relative.

i.e. that the RELATIVE risk reduction is ~10%
But the ABSOLUTE risk reduction is ~0.2%.
RRR = ARR divided by control arm risk: 0.2%/2.3% is about 10%.
Start with a deck of 200 cards. Every year, you shuffle and draw a card. If it is "the card of death", you die. If not, you live and discard the card.

If you pay us $0.03 per year, any time you draw the death card, we will give you a CHANCE to ignore it.

If it comes up 1 to 9, sorry you still die.
(What do you expect for $0.03?)
If you have paid Francis Industries your ~$10 per year, what is the probability of dying that year? Remember we cancel 1 in 10 death cards.
Eventually everyone will die.
Twenty-somethings complain at nightclubs, "This is sh!t. I've never met anyone who drew a death card. And yet I am paying these scamsters $10 a year".
Those people who escape death by that means, don't escape it forever.
So EVENTUALLY everyone dies in the "prevention" and "no prevention" arms.
My customers do JUST A LITTLE BIT better.
James Howard and I argued over whether to do the computation in R (his preference because he is trendy) or Matlab (mine, because I am a dinosaur).
So we did it in both languages!
We showed everything openly in our paper
openheart.bmj.com/content/3/1/e0…
The full code in both languages is in Supplementary Appendix
openheart.bmj.com/content/openhr…
The software can be set to address any risk stratum.
If you know Matlab (or Octave) or R, or can read the fairly simple code and put into a language of your choice, go ahead and play.
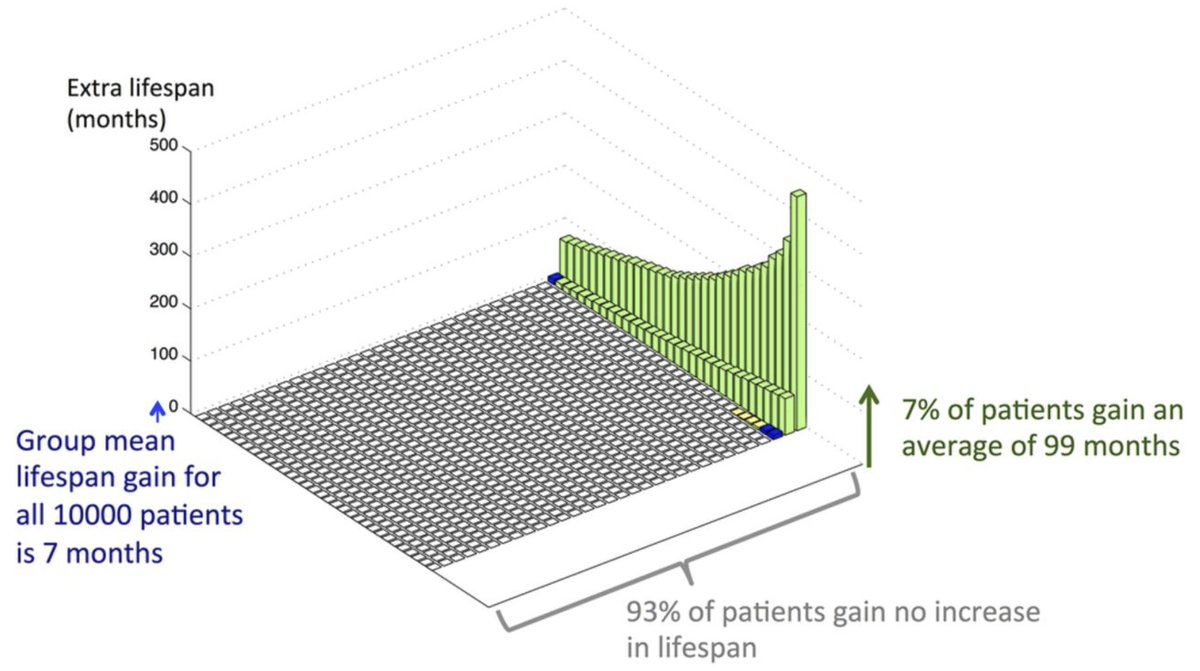
Let me say that again. 9/10 people die on the same day they were going to die anyway.
They gain nothing.
How can this be?
How can 90% of people gain nothing, but the overall group gain an average of 1 year?
Pause for questions before we move on to NNT. 2 hours.
I am not sure where your figures came from. They are not correct.
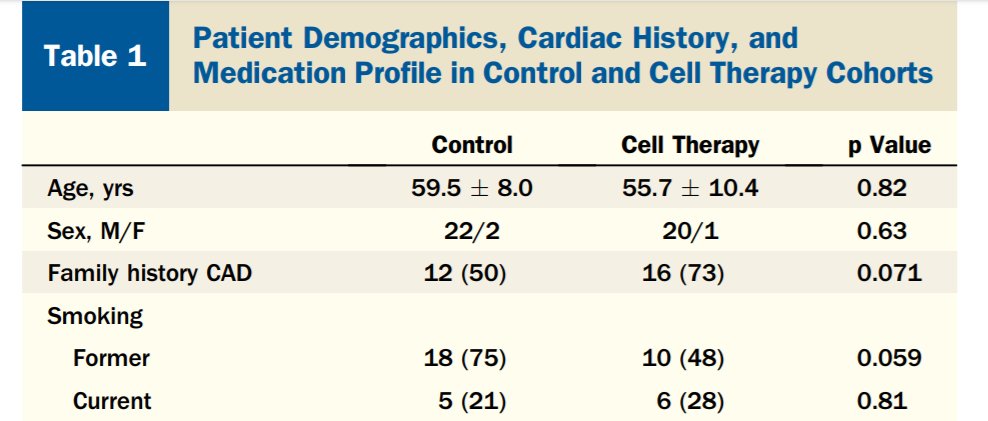
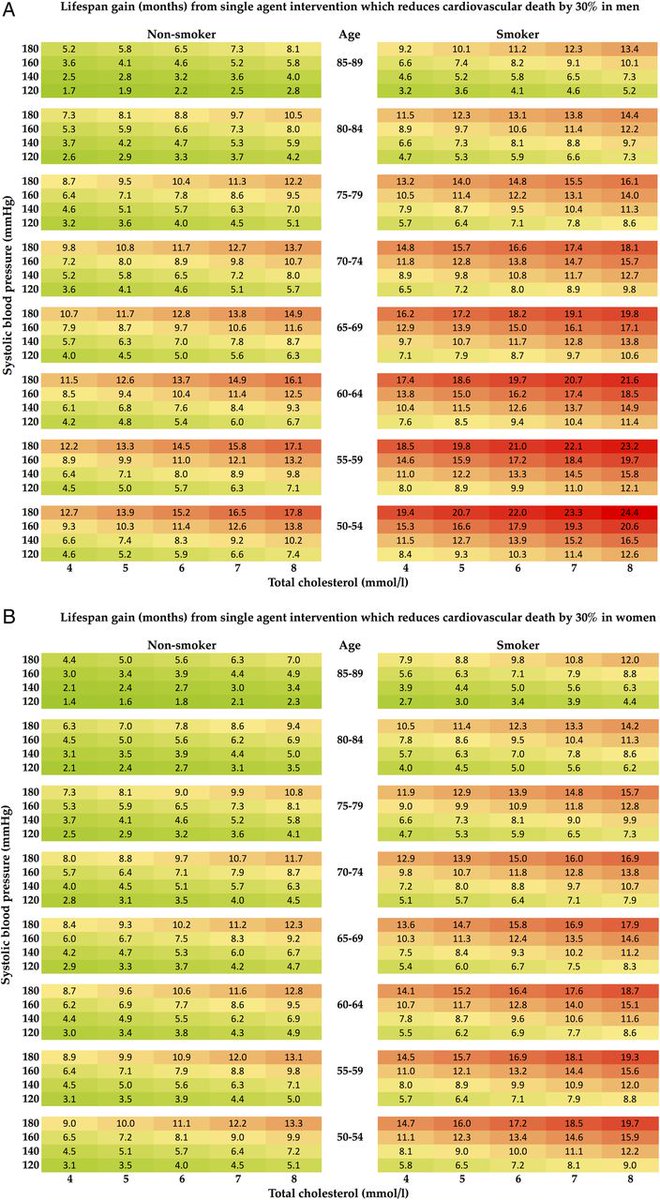
Very roughly if you start 1000 average 40 year old men on a preventative therapy that prevents 1/10 of all fatal events (think of it as a partially effective bullet proof vest),
Is this obvious?
Either they were non-cardiac (approx 700 of the 1000) or were cardiac but weren't prevented by the statin (200 of the 100).
That leaves 100 deaths that were "prevented".
How much later? The calculation shows you. On average VERY ROUGHLY 10 years later.
So overall the lifespan extension is about 1 year averaged over all 1000 people.
900 get nothing.
100 get 10y.
"Can we work out who is going to be one of the ones who gets lifespan extension, and who doesn't, so we can just treat them and save annoying everyone else?"
YES! We do this by running RCTs of statin and see who has the best hazard ratio.
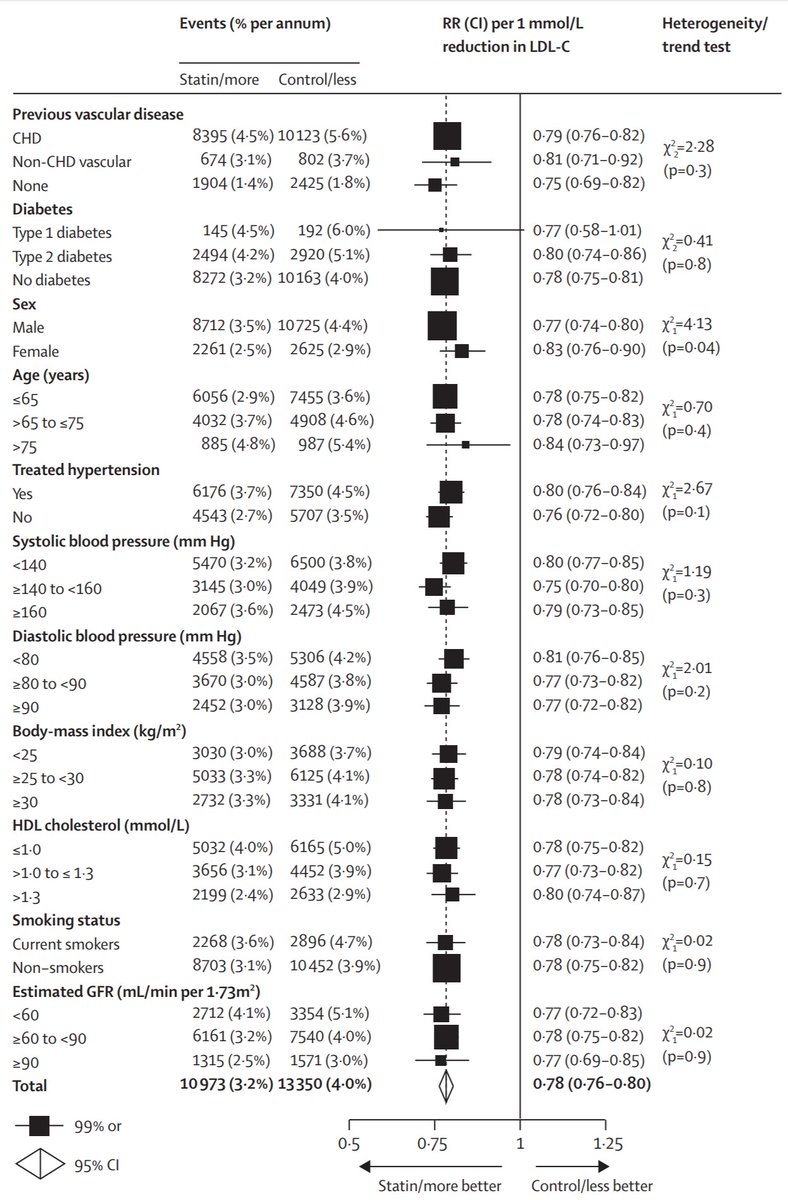
It's just that it is VERY GOOD for this type of question.
They tried slicing the data by many methods that we use to stratify risk.
Age, BP, HDL etc.
Which of these found slices that DID NOT get benefit?
Instead of looking forlornly for the "no benefit" 90%. Let's look even for people with just "LESS benefit".
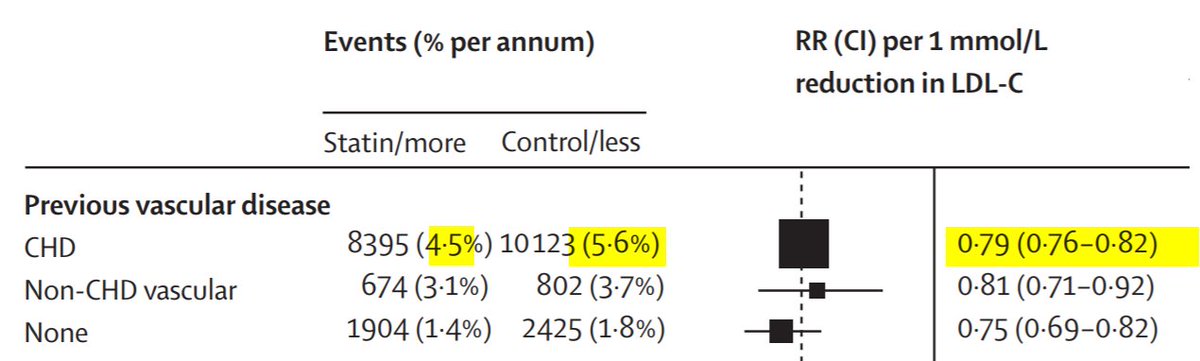
Look at the right column, and its P values. Only one suggests a notable difference in the risk ratios. Which categorisation?
A Night and Day: worked in one, totally failed in other
B Worked in both, but twice as much in one than other
C A bit better in one than the other

Evidence of this is here (using IHD _death_ rates, from the World Health Organisation via Finegold ncbi.nlm.nih.gov/pmc/articles/P…)
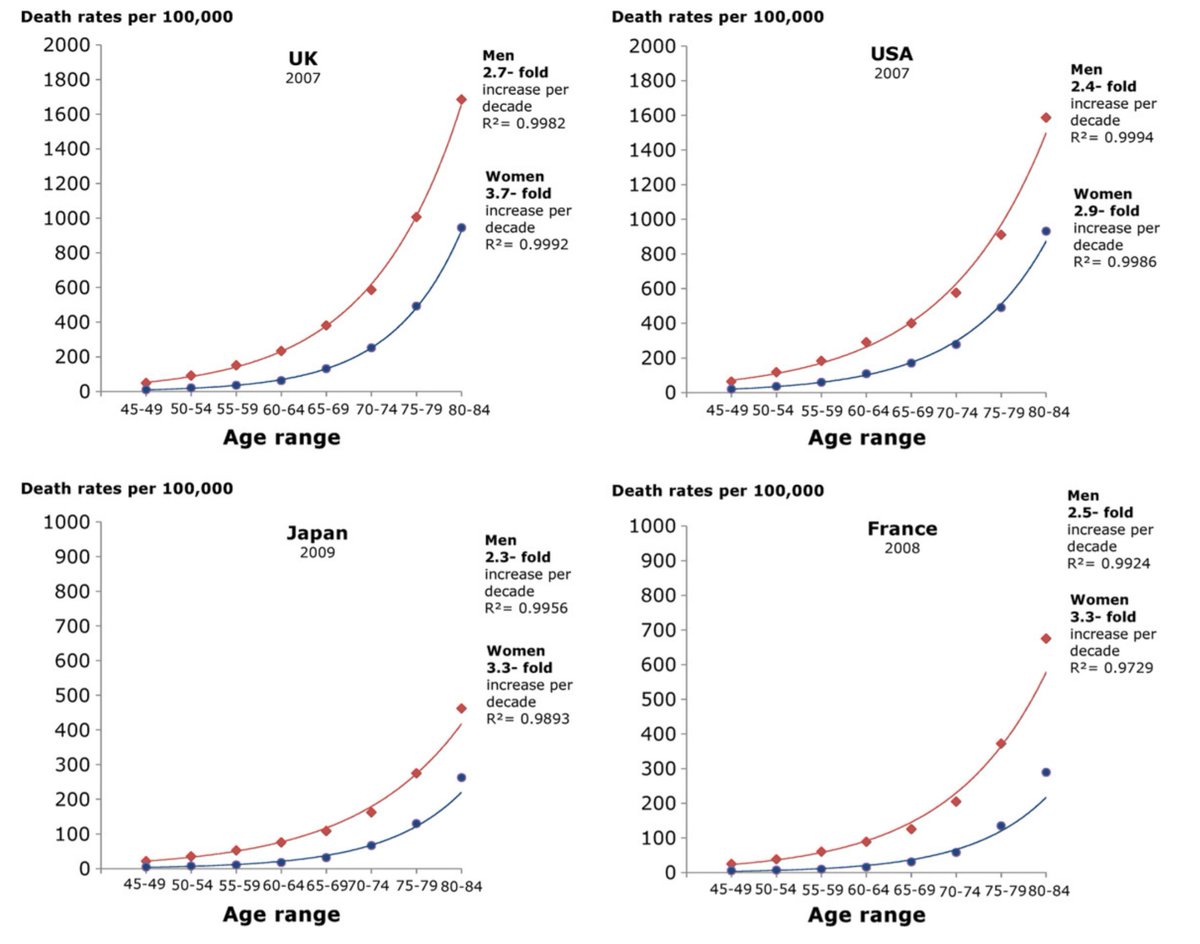
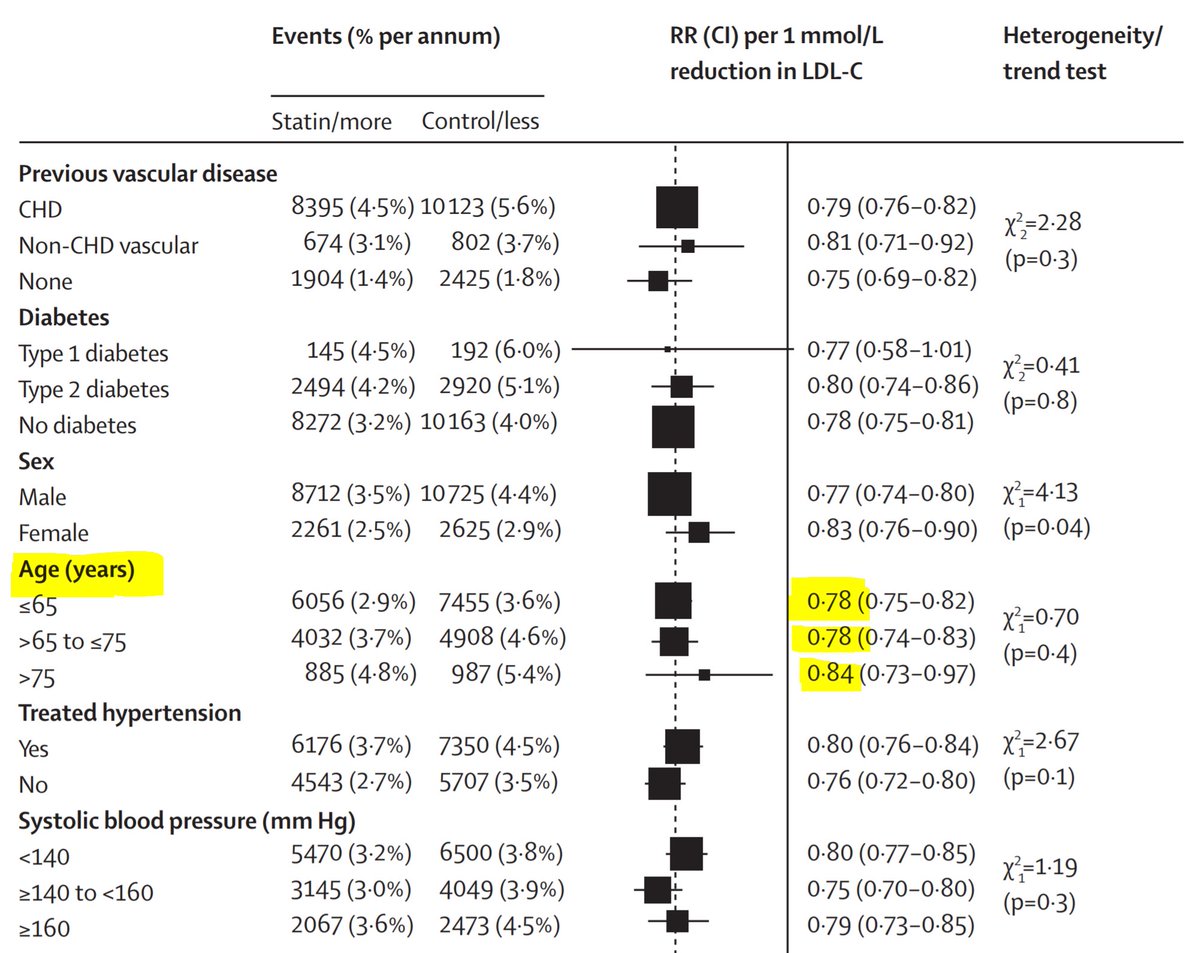
Definitely DOES NOT get 3-fold weaker with 10-year age increment. 0.78 (=22% below 1.00) would have to become 3 times closer to 1, i.e. 21%/3 = ~0.07 away, i.e. 0.93. It's not that.
there is a three-fold increase in IHD rates
and the RISK RATIO with statins stays approx 0.80, so what happens to the ABSOLUTE RISK REDUCTION with statins?
But I am NOT arguing it is anything to do with LDL, HDL or anything in particular.
Statins are death prevention tablets.
People debate the mechanism, some fluently with immense knowledge of the data (@skathire) and others do it half-wittedly with limited grasp of even basic logic or arithmetic.
15 years.
Rest assured, statistical friends, the paper makes clear that this is PURELY the result of PROBABILITY in action. In the paper there is NO way to identify who will be in the 7%.
All the information is in the ratio between bullets and chambers.

Still you can't meddle with the randomness, only identify the probability. Until we can stratify people to probabilities of 0 or 1, this calc will hold.
Nobody wants to get a question from BOTH Ethan Weiss and Sek Kathiresan.
Like giving a math talk at a primary school and finding Albert Einstein and Isaac Newton raising their hands. "We were discussing, couldn't agree, and wondered your opinion..."
#NotGoingToBeEasy 🤔

Better keep quite and not admit to not know what I am talking about.
Prize goes to the most convincing.
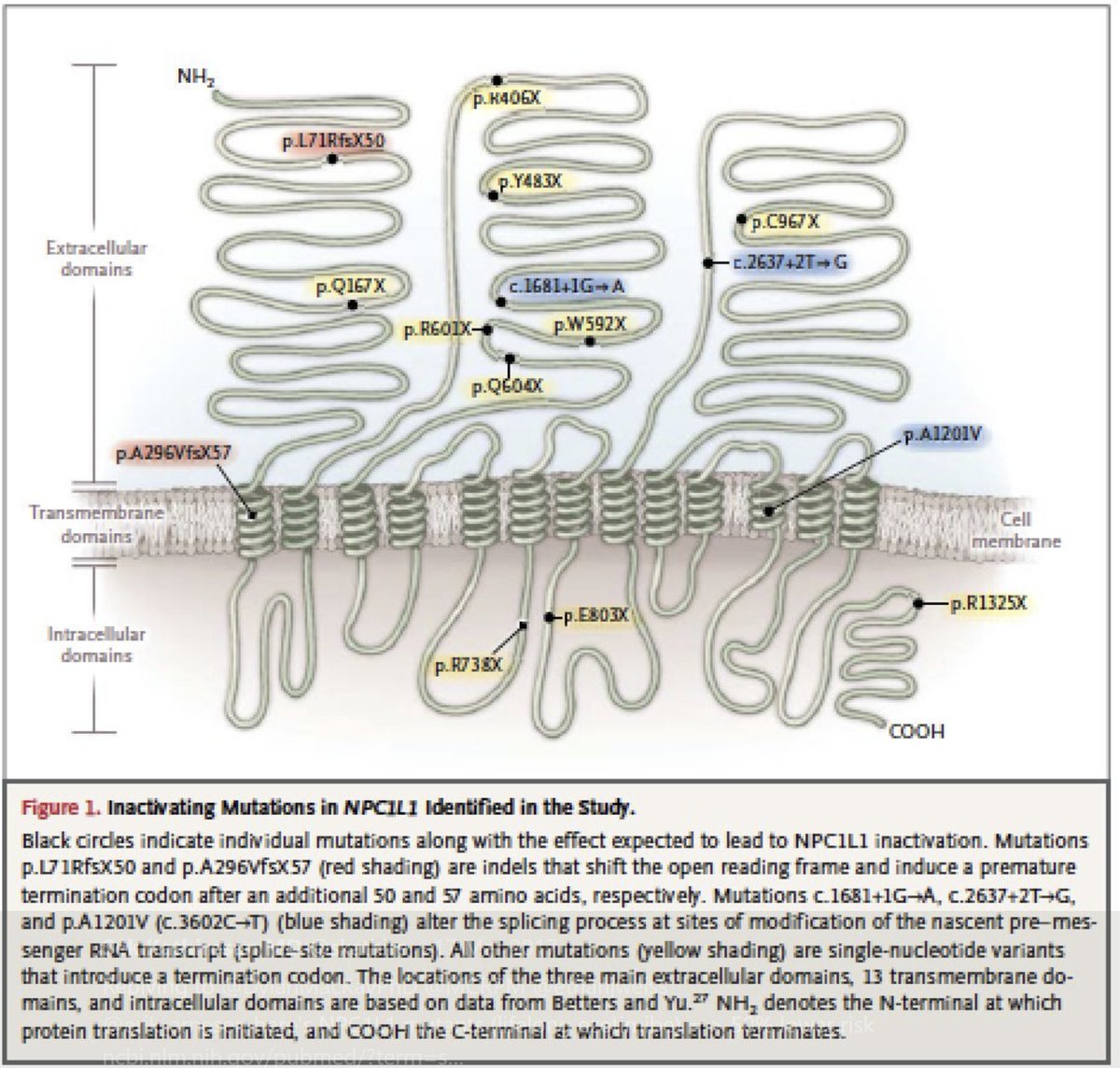
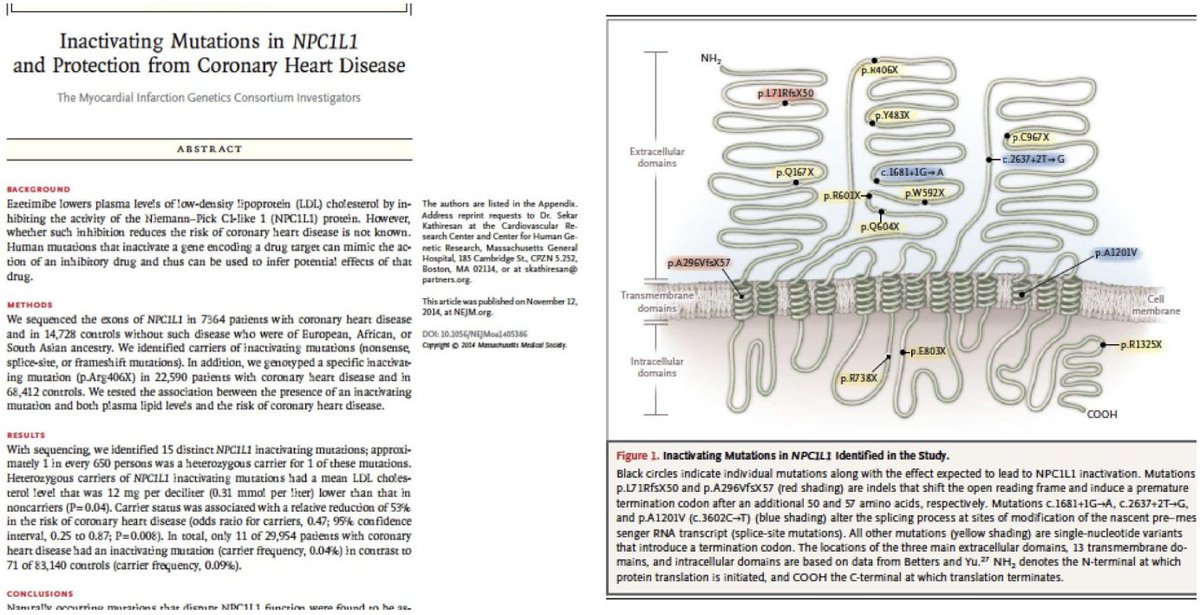
(a) There is a gene defect resembling the effect of ezetimibe
(b) Present in 1 in 650 people
(c) Drops LDL 0.31 mM (12 mg/dl)
(d) HALVES coro disease
That's a lot bloody better than bloody ezetimibe, whose IMPROVE-IT trial had to be dragged on for year upon year until the investigators themselves had nearly died.
OK his question:
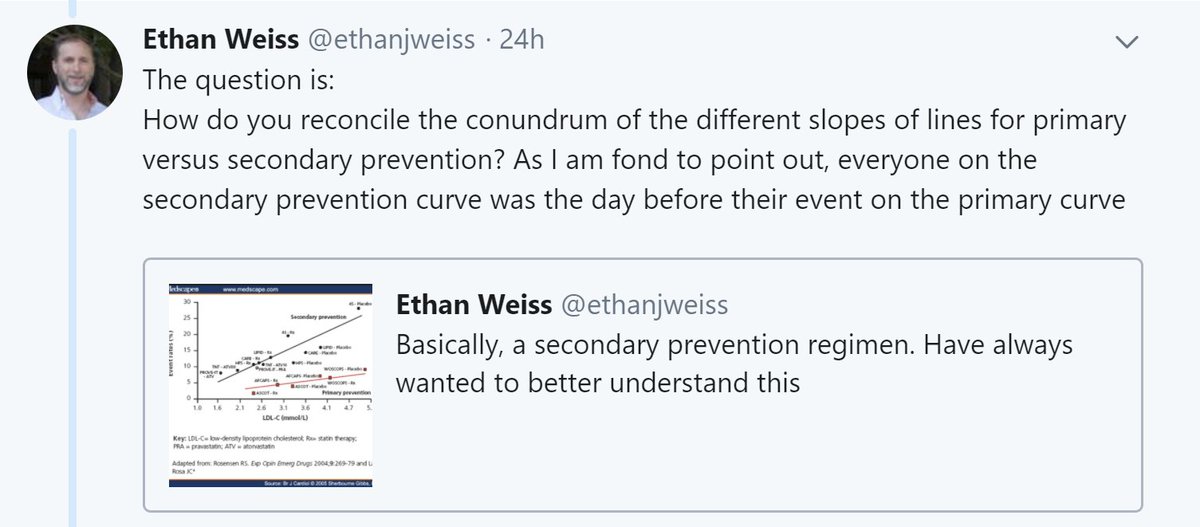
'If the Ezetimibe gene is so amazingly brilliant that it halves coro disease, how come "acquired Ezetimibe" is so feeble?'
Is it because people don't take their meds?
The IMPROVE-IT trial will instantly answer this.
Am surprised people didn't look. I train my team not to just make up stuff: look to see if someone has published a proper scientific report.

In IMPROVE-IT, how much did the ezetimibe, prescribed at 10mg od, reduce LDL?
Is this LESS than the 0.31 mM drop seen in Sek's NEJM paper of "Genetic Ezetimibe"?
HINT. In snapshot above, it says "hazard ratio, 0.936"
But the DRUG lowers CV events by LESS (6%) than the gene (~50%).
The gene has a lifetime to influence the pathway.
The drug can only start when you start to take it.
Sadly, we keep assessing risk OVER A LIMITED TIME for primary prevention.
Sad but true.

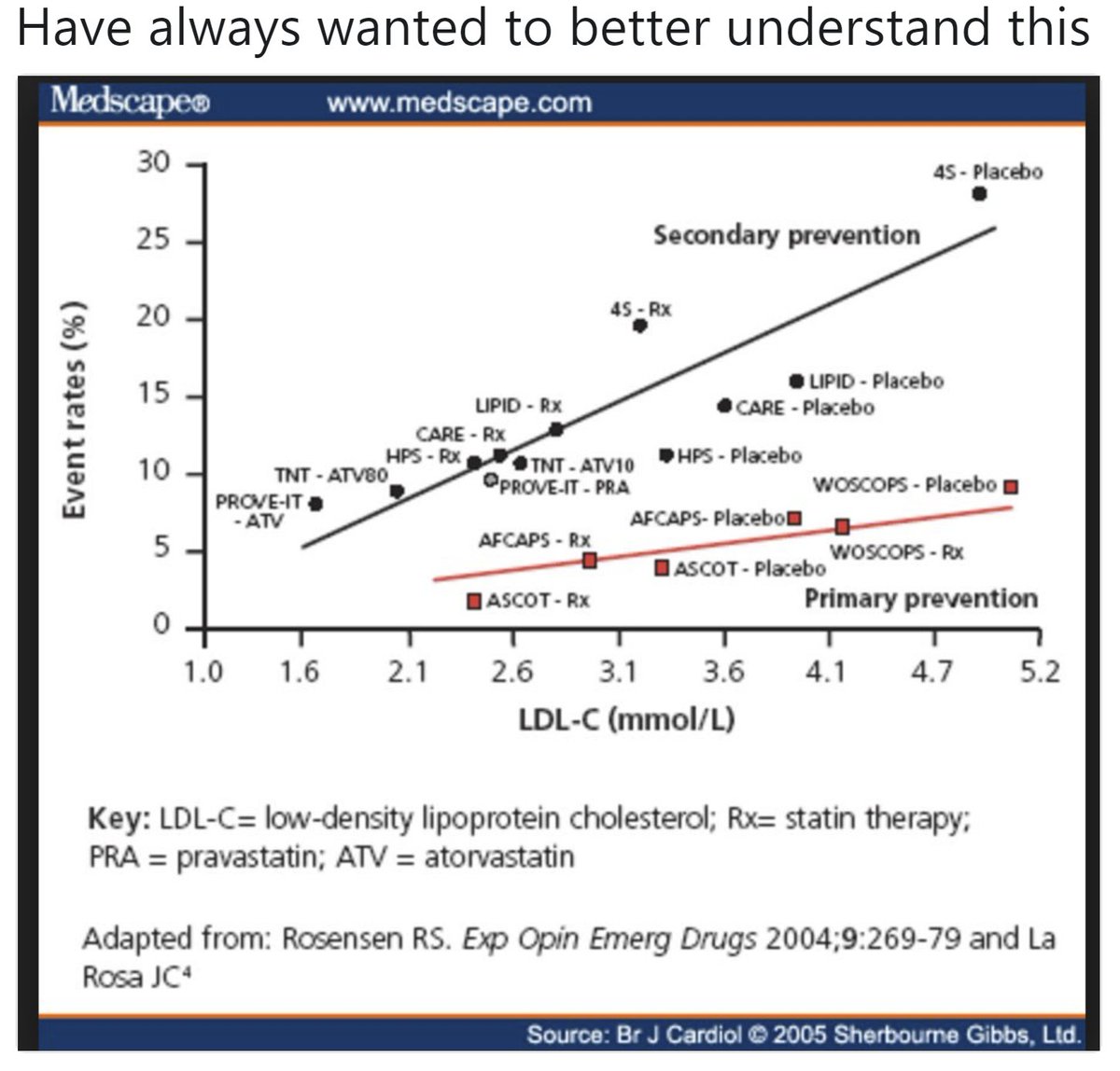
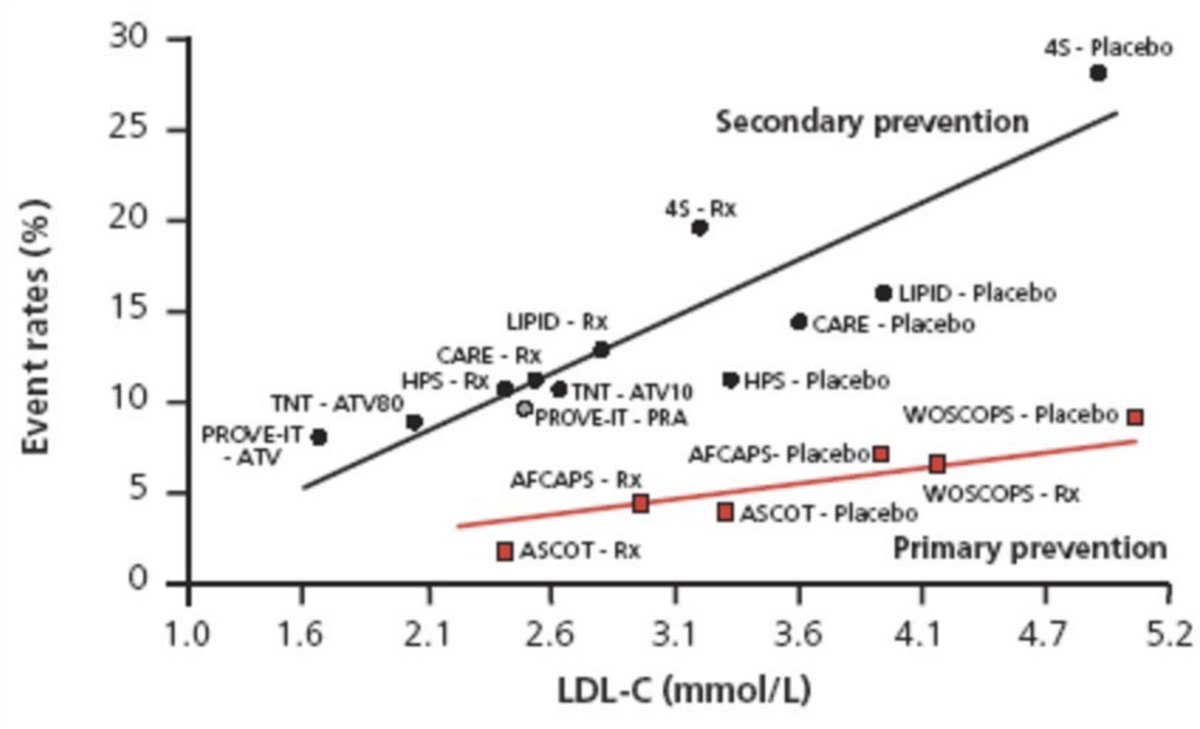
The "Secondary" set is is just the "Primary" set with many people removed.
Gulp.
I reckon the top line POSITION at any point on the x axis is about 3x the bottom line.
And I reckon the top slope is about 3x the bottom slope.
Of course I might be talking sh!t. Can anyone calc?
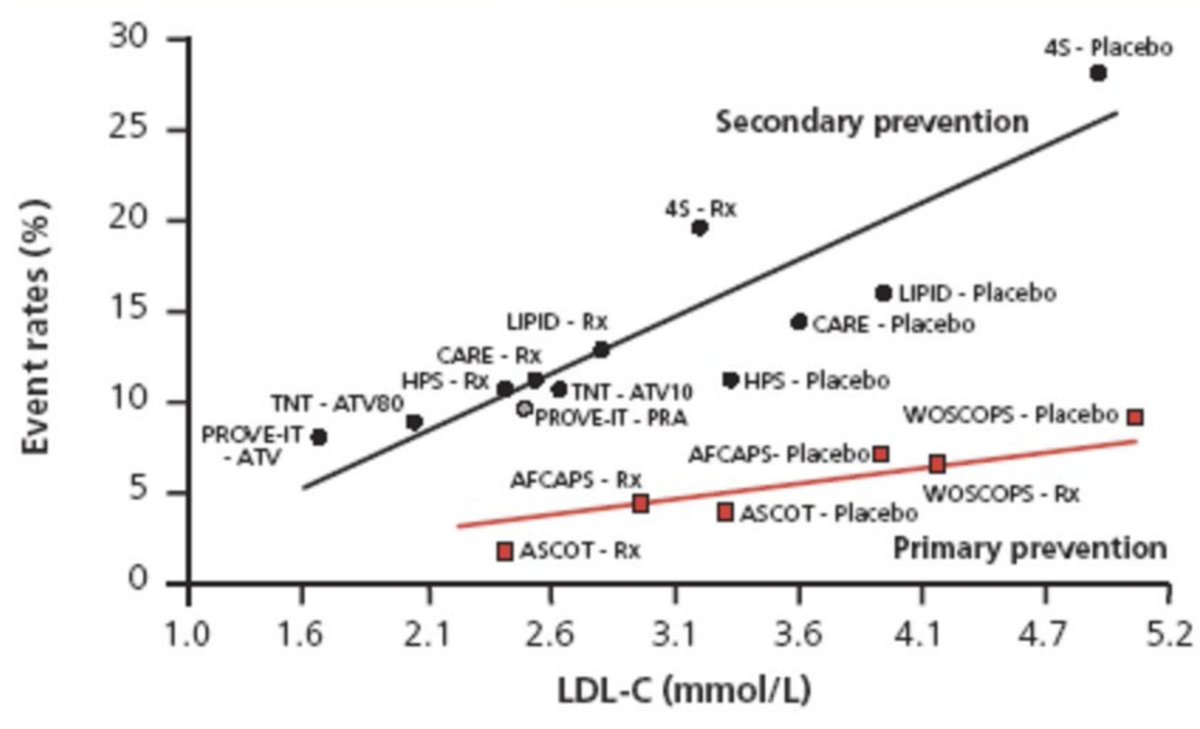
Going for secondary, "gets rid" of them and leaves us with an enriched 1/3 who have 3x the risk of the overall group, and 3x the sensitivity to LDL etc
Fun for a fellow to do? Anyone with you Ethan or you Sek who might be interested?
It's basically so crazy that I bet nobody has done it. I like such papers.
==============
NNT strikes back! (not)
An explanation for NNT that even statin deniers can understand!
Please use this info to deal with people who try to kill your patients for fun and profit.

Published in Br J Sports Med, so must be OK
Applying F.I.B., what can Jonas get the crenulation rate down to?
"This will cost us a fortune."
Remember, this is in the UK, where we can't just spend an extra few tens of thousands, and stick the patient with the bill.
"How many patients do we have to treat to prevent one crenulation?"

If we treat 100 patients, how many people do we save from crenulation ?
The crenulation all occurs within the first 24 hours. After that the molecule CREN-Kinase (pictured below) disappears.
No crenulations occur in the remaining 29 days.
I do a longer term study, lasting 1 year. No more crenulations occur.
what is the ABSOLUTE risk reduction (ARR)
and the RELATIVE risk reduction (RRR)?
Sorry to labour but we MUST get this right now. Vital.
"But on the Paediatric ward, Francis Linear Intergrated Medicine provides a Flow-Line Arbitrometric Motivator", which greatly reduces discombobulation."
If we treat a hundred children with FLIM-FLAM, how many fewer discombobulations would we have?
We get TEN prevented if we treat 100.
So to get ONE prevented we must treat ....
In the Paediatric Emergency Ward, what is the NNT to prevent one discombobulation?
NNTs:
For a condition that is short lasting and you either GET or DONT GET something bad, we can give a treatment and calculate the difference in bad things happening.
If the ABSOLUTE difference is 1/100, you need to treat 100 to prevent 1 event.
In fact if you can write the ABSOLUTE difference as 1/SOMETHING, the NNT is "SOMETHING"
Suppose primary PCI (versus fibrinolysis) reduces 30 day mortality from 8% to 7%.
What is the number needed to treat to prevent one death within 30 days?
Does it give any different information from the ARR (Arrrr, shiver me timbers, mateys!)

NNT is more advanced than ARR. (No beard or parrot)
NNT is more flexible than ARR. (Can express complex situations)
NNT is statistically preferable by clever folk like Frank Harrell @f2harrell
NNT give identical information to ARR
NNT = 1 / ARR
So it is NOT true that it is "more advanced".
You just say that.
But try it with NNT
NNT is 10 (95% CI, er, oh bollocks.... to 4)
That's not flexible, that's inane.
Without Rx, 80%.
With Rx, 20%.
ARR = 60%
NNT = 1/0.6 = 1.667 .... eh?
It is NOT more flexible, unless you like confidence intervals that wrap round to infinity and back again. Maybe you are an astrophysicist and like this sort of thing. I don't.

Albert Einstein
Br J Sports Med
For example, instead of 0.01% you might say 1/10,000. That's just an ARR.
If you want to say that is an NNT of 10,000 but this just adds another layer of verbiage.
A group of 7 ER physicians, together with 3 other people, have set up a site to idolise the NNT.

No survival curves, no nothing. You are either OK or you are stuffed.
For those situations ARR works well. If your ARR at 24 hours is 2%, it stays 2% permanently.
But where statin denialists go wrong is in trying to apply this where it cannot usefully be applied. To CHRONIC STABLE diseases with progressively varying numbers. Lets see why.
I enrol a group of patients, with a 1% annual mortality.
What would the graph in the CONTROL group look like over 4 years?
It would start at 0% mortality at 0 years.
At 4 years, what mort?
Remember it has a RELATIVE RISK REDUCTION of 10%.
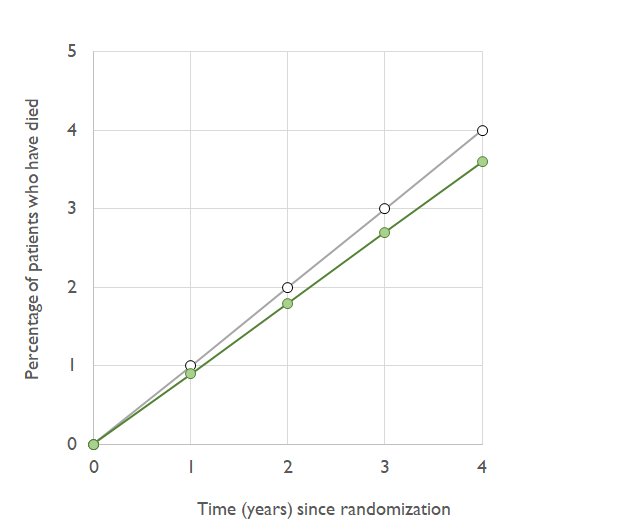
Risks are 4% in control, and 3.6% in statin.
HINT
Look at the graph. The vertical gap is smaller at 2 years. How much smaller (super-hint, how much smaller is it if you go back to 0 years?)
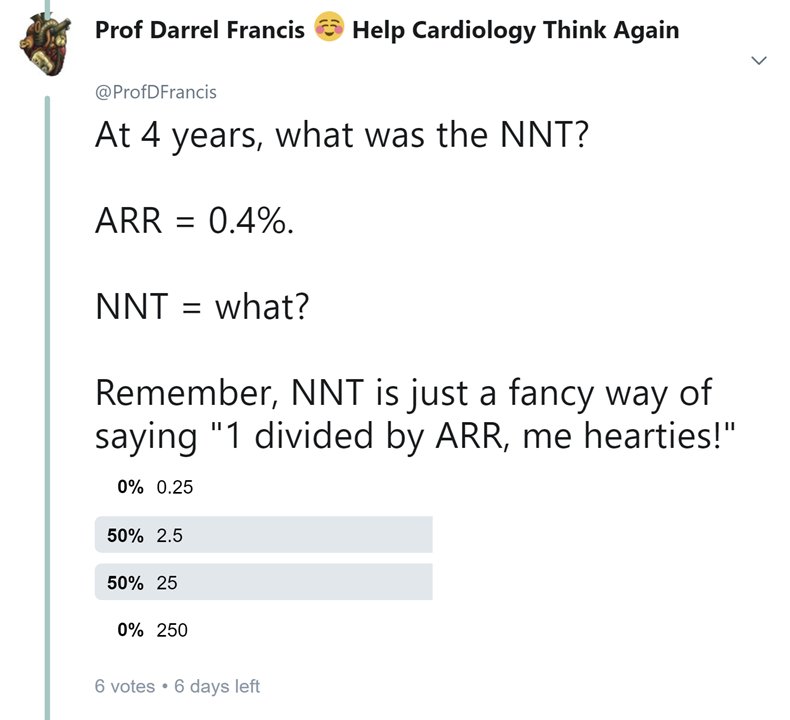
ARR = 0.4%.
NNT = what?
Remember, NNT is just a fancy way of saying "1 divided by ARR, me hearties!"
NNT = ?
NNT = ?
--sigh--
Aseem Malhotra, come along and shoot me please.
First I will sign your anti statin manifesto with Sir Bufton Tufton who wants a public inquiry into arithmetic. Then I will help Maryanne Demasi with her Photoshopping.
Then kill me please.

Sit back, relax, think back to primary school, OK? Happier, carefree days. Only easy stuff to do.
100 divided by 2 = 50
100 divided by 1 (a smaller number) = something MORE, yes, i.e. 100
so
100 divided by 0.4 (even smaller) = something EVEN MORE
I now know why you couldn't smack Malhotra, Demasi, Bufton Tufton, and the other nitwits, in the face swiftly. You weren't good at reciprocals.
That's why they settled on NNTs to bamboozle you. You are not good at 100/n.
2 y. ARR 0.2%. NNT = 500.
4 y. ARR 0.4%. NNT = 250.
Now, can you guess what would happen if we extrapolated the survival curves to continue?
8 y. ARR what, NNT what?
Which is true?
To the nearest %.
But that is why we all need to get fluent in percentages. Given the correct answer to the tweet immediately above this, this is why we have, effectively, morons, running rings round us. We don't have the wit to keep them off.
We need to get better.

Think back to school. "%" is just shorthand for "/100", that's all, nothing more subtle.
1% is not, NOT, N*O*T 1. It is 1/100 or 0.01.
Even Aseem Malhotra can understand this and it is enough to leave us bemused.
1/ARR = 1/ (1/100): that is what should pop up in your mind straight away.
That's obviously 100, not 1.
We *need* to get fluent so we can deal with the propaganda put out by the statin-denialist nitwits.
Will you keep the faith with these tweetorials?
If things progress as before, by 10 years, there is what size difference between the two curves?
What absolute risk reduction?
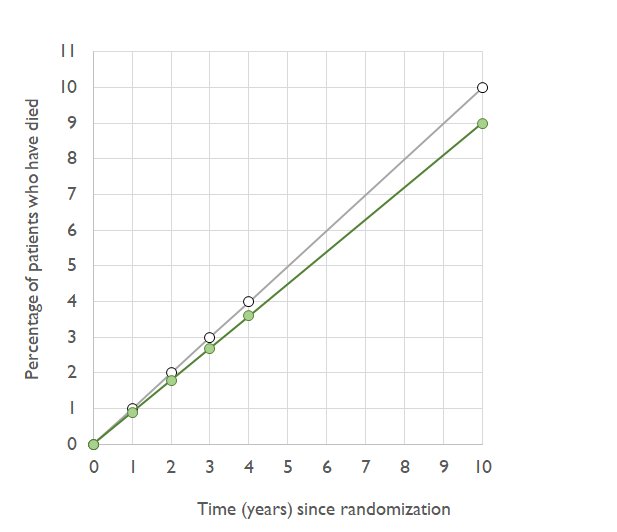
10% (thats 0.10 for people who can't remember what % means)
9% (or 0.09)
The ARR is the difference between them (use the right hand figures if keep forgetting what % means)
What is the NNT?
As the years progress, you will always have slightly better chance of surviving a year in the statin arm than placebo...
You can calculate how much longer a lifespan you get in the active arm.
The calculation is shown in full here, in 2 computer languages (as Shun-Shin and Francis fought like children over which was "better")
openheart.bmj.com/content/3/1/e0…
As time passes, ARR increases, and NNT shrinks.
Eventually everyone gets old and dies, ARR shrinks again (as mortality in both arms approaches 100%) and NNT goes back to infinity.
ARR and NNT vary across the entire time course!
Life's too short.
Focus on the RATIO.
CTT 2010 again:
That is also in our paper "Distribution etc."
openheart.bmj.com/content/3/1/e0…
In practice, as we said, WITHIN THIS CALCULATION about 90% of people die of SOMETHING ELSE (so statins don't help) or die of a heart attack despite statins (so statins don't help)
1000 people
700 die of non-cardiac disease (no effect on them)
Of the remainder, 200 still die on their original date as they would without statin, and the remainder die later.
So 100 people live longer.
How is it possible?
Becacuse they live 70 months longer, on average. 6 Years.
Approx 90% chance that you will die on the day you would have died without the statin, and about 10% chance that you will live longer - by 5-10 years.
But if people, who are not your doctor, tell you NOT to do that I am here to back you up, because I want you to live longer if you want to live longer.
It is not nice, but they are not nice.
And I, most definitely, am not nice.
g'night!