1. "Je suis assis à mon bureau"
2. "[Je] suis devant mon ordinateur"
3. "[Je suis] face à la fenêtre"
1. "Je suis assis à mon bureau"
2. "[Je] suis devant mon ordinateur"
3. "[Je suis] face à la fenêtre"
1. Modéliser les zones correspondant à chaque élément de localisation
2. Combiner les zones entre-elles.
1. Le point de départ
2. Une durée
en.wikipedia.org/wiki/Naismith%…
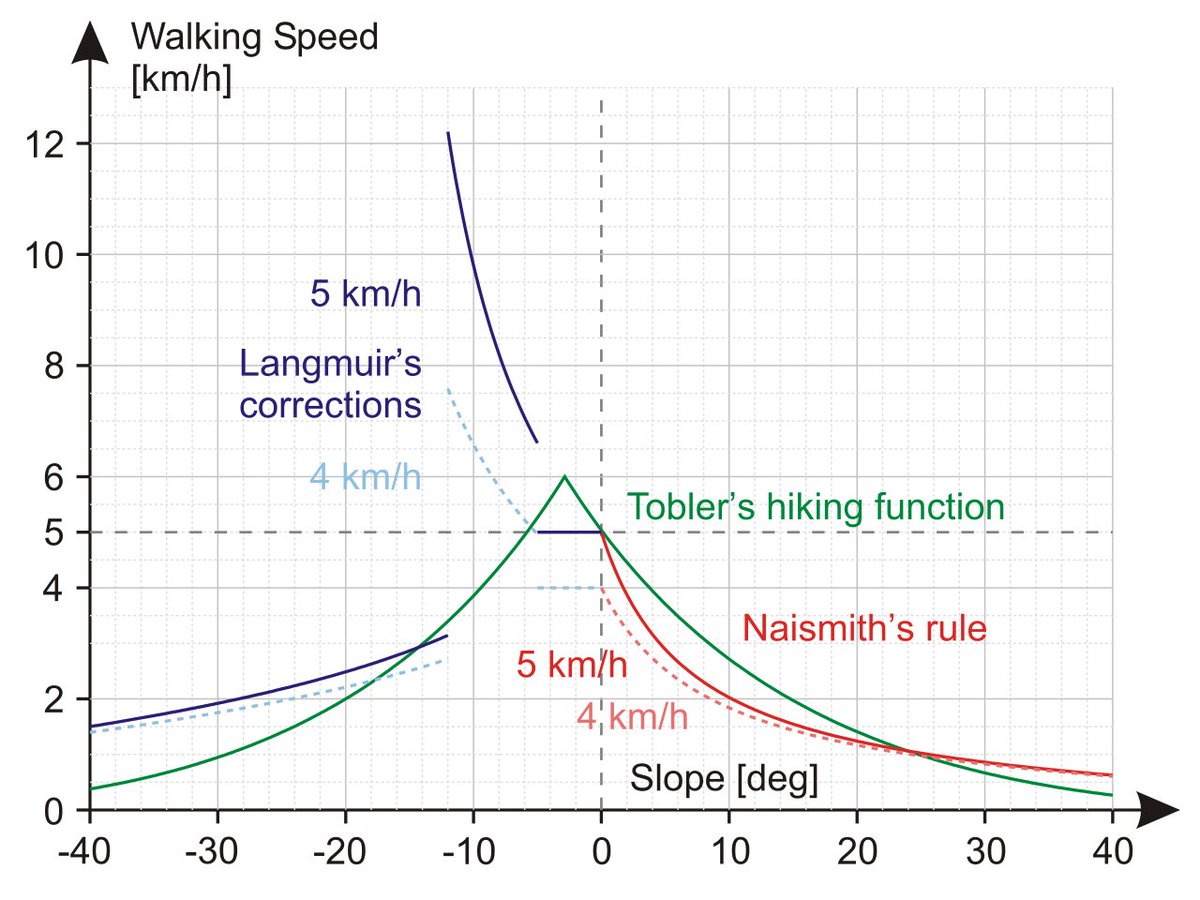
"j'ai marché plusieurs heures sur un chemin à partir de Bourg d'Oisans "














