Thread by @choffstein

1/ A Thread on Rebalance Timing Luck

- What is it?
- Does it matter?
- How do we solve for it?

2/ Rebalance Timing Luck ("RTL") is the unintended performance consequences due to the choice of when to rebalance a portfolio.

One might argue it is the result of unintended market timing.

3/ AFAIK, it was first documented by Blitz, van der Grient, and @paradoxinvestor in their 2010 paper Fundamental Indexation: Rebalancing Assumptions and Performance (papers.ssrn.com/sol3/papers.cf…)

4/ Within, they demonstrate the performance dispersion that results due to the simple choice of when to rebalance a fundamental index portfolio.

5/ They suggest the use of "overlapping portfolios," achieved by equally dividing your portfolio into sub-portfolios that rebalance on different dates.

This is also called "tranching" or "staggered portfolios."

6/ @RA_Insights ultimately ended up implementing this exact solution: research.ftserussell.com/products/downl…

7/ As a side note, it is worth pointing out that while uncommon in public markets, this is a very common approach to implementing private investments.

Investors acknowledge market cycle risk and therefore tend to invest in multiple PE or VC funds over time to diversify the risk.

8/ At Newfound, we first started writing about this effect back in 2013, having discovered it independently.

We wrote about it with respect to tactical portfolios, but over time appreciated that it affected almost *all* portfolios with a fixed rebalance schedule.

9/ Our research culminated in our paper "Rebalance Timing Luck: The Difference between Hired and Fired" which was published earlier this year

jii.pm-research.com/content/early/…

10/ We sought to address three points:

- Demonstrate that timing luck impacted something as simple as a 60/40 portfolio

- Prove that overlapping portfolios were the optimal solution

- Derivate an equation to estimate timing luck ex-ante

11/ The first was rather easy, and really only required us to generate different 60/40 portfolios rebalanced at different times in the year and plot the dispersion in their performance.

Remember: the only variable here is *when* portfolios are rebalanced.

12/ Next, we proved that overlapping portfolios were an optimal solution.

I won't go into the proof here, but suffice it to say that I think the result is pretty intuitive. It's just diversification!

13/ Finally, we wanted to derivate an equation for estimating the potential impact of timing luck.

The equation we derived is:

L = 0.5 x (T / F) x S

14/ Here L is timing luck, T is annualized turnover, F is the # of rebalances that occur per year, and S captures how different our portfolio can be from one rebalance to the next.

15/ S is probably the hardest to interpret, so consider this example: a high turnover momentum portfolio.

If totally unconstrained, S will be very high. If highly constrained (e.g. implemented intra-sector), S will be much lower.

16/ The intuition here is that high-turnover strategies, with few constraints applied, and which are rebalanced infrequently will have very high timing luck risk.

17/ I want to stress here that while the choice of rebalance frequency does impact timing luck, it should really be derived as a function of signal decay speed and cost.

e.g. a momentum portfolio likely has to rebalance more frequently than a value portfolio.

18/ In this week's commentary, I decided to tackle the empirical evidence of RTL's impact on smart beta returns by constructing 4 different styles, 8 concentration levels, and 3 different rebalance frequencies.

(Still with me? Here's a sneak peek: digioh.com/em/10484/17010…)

19/ Using these different portfolios, we can estimate the realized performance dispersion from a timing-luck-neutral implementation.

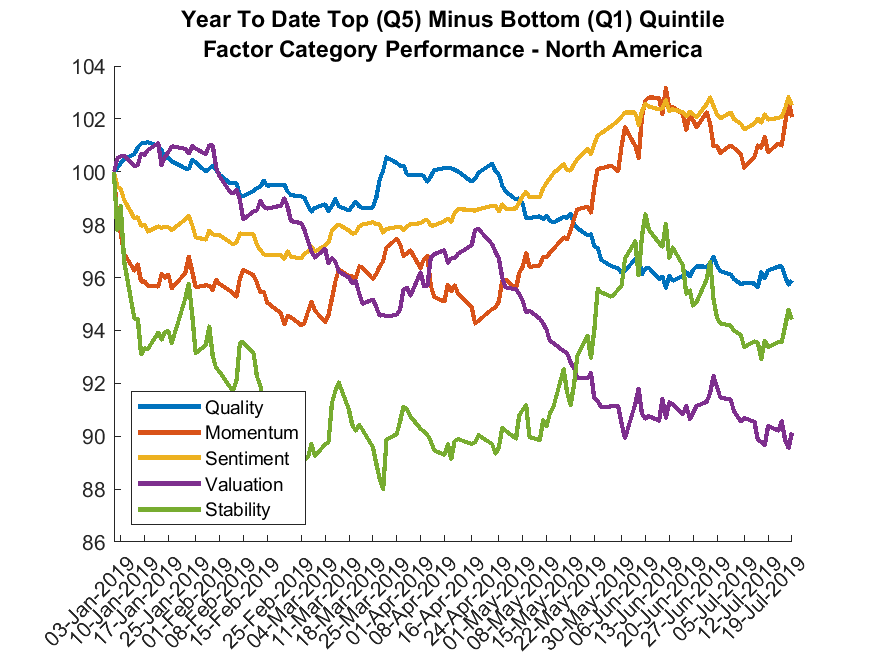
Our expectation is those strategies with higher turnover, less frequent rebalancing, and fewer constraints will exhibit more rebalance luck.

20/ And that's exactly what we found.

21/ But perhaps what is most staggering is the sheer magnitude of the timing luck here.

For a 100 stock value portfolio rebalanced semi-annually (hmm... sounds like most smart-beta products...), we're talking about 2.5% *per year.*

22/ And that's as measured against a timing-luck neutral benchmark. We need to multiple that by SQRT(2) to compare two non-neutralized portfolios.

Just look at the dispersion realized in Momentum. We highlight the dispersion in the APT-OCT vs MAY-NOV implementations.

23/ But these are all hypothetical, right? Well, let's replicate some real-world examples.

Here are the various implementations of S&P 500 Enhanced Value, Momentum, Low Volatility, and Quality.

23/ Perhaps the dispersion is made more clear by looking at their annual returns.

25/ The risk here is not really volatility, but a dispersion in terminal wealth.

Choose the wrong rebalance date and you end up with very, very different results.

26/ In conclusion: "when" is an under-discussed form of risk.

Or, put another way, "when" is a meaningful axis of diversification that we ignore at our own peril.

27/ I believe this evidence suggests that comparing strategies that are not timing-luck neutralized, or managers against benchmarks that are not timing-luck neutralized, is a fruitless endeavor.

Far too much noise comes from the impact of "when."

28/ Some follow-up data Q&A I usually field.

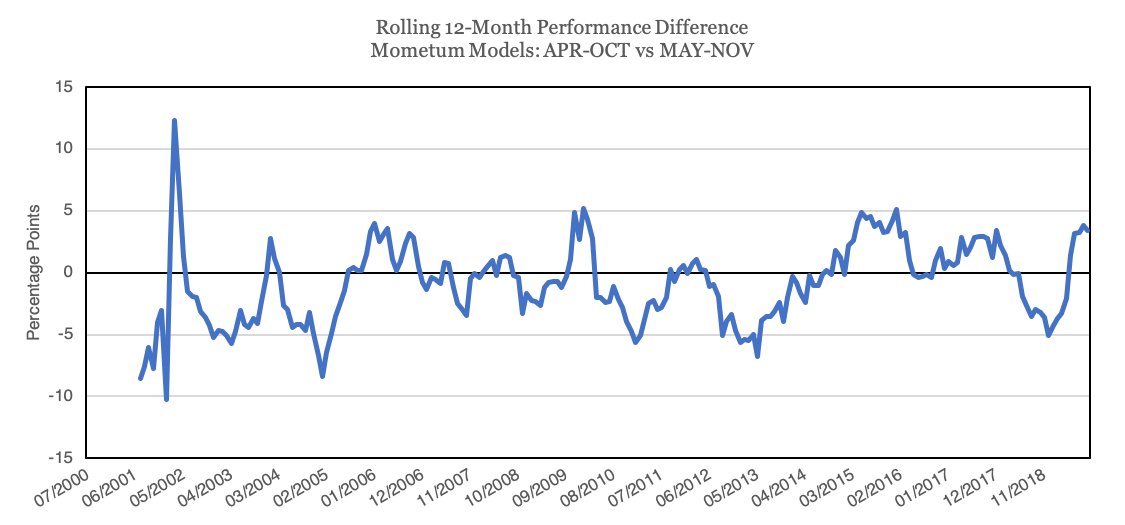
Q: Are the results mean-reverting?

A: Augmented Dickey-Fuller tests suggest no. Random, but not mean reverting. This appears to be a totally uncompensated risk.

29/

Q: What about seasonality?

A: Bootstrapped simulations suggest that there is no meaningful edge in selecting one rebalance date versus another.

But if there is, this data suggests the Sharpe is likely small.