Thread by @tyrell_turing

1/ Need a distraction from the pandemic? It's #tweeprint time!!!

I'm very excited to share here with you new work from myself, @NeuroNaud, @guerguiev, Alexandre Payeur, and @hisspikeness:

biorxiv.org/content/10.110…

We think our results are quite exciting, so let's go!

2/ Here, we are concerned with the credit assignment problem. How can feedback from higher-order areas inform plasticity in lower-order areas in order to ensure efficient and effective learning?

3/ Based on the LTP/LTD literature (e.g. jneurosci.org/content/26/41/…), we propose a "burst-dependent synaptic plasticity" rule (BDSP). It says, if there is a presynaptic eligibility trace, then:

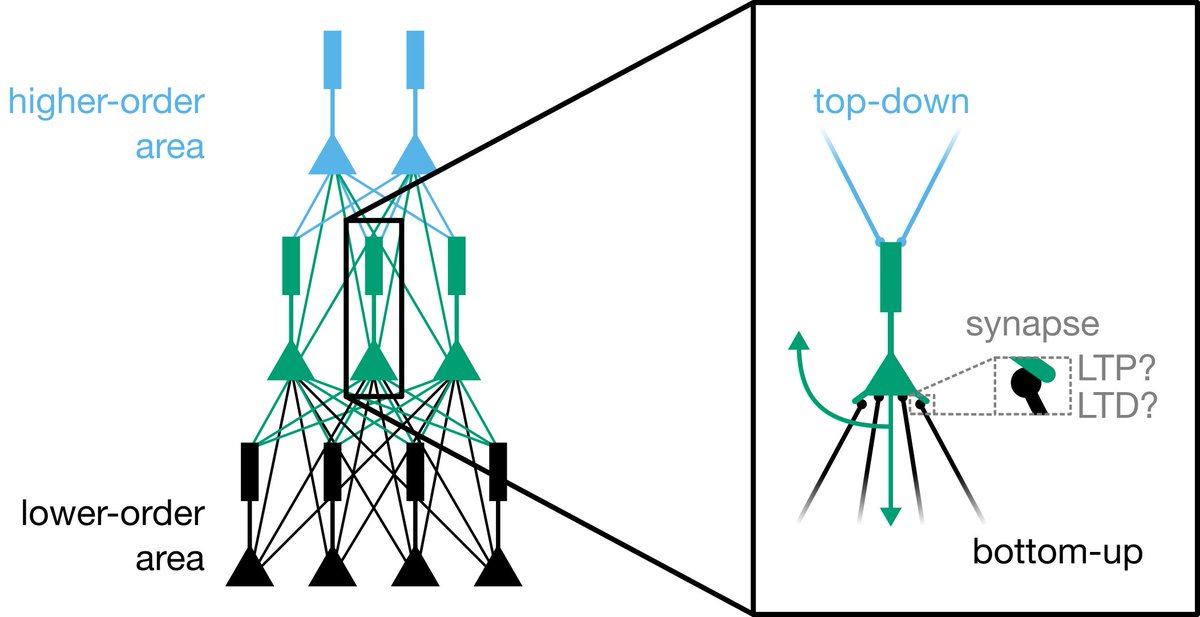
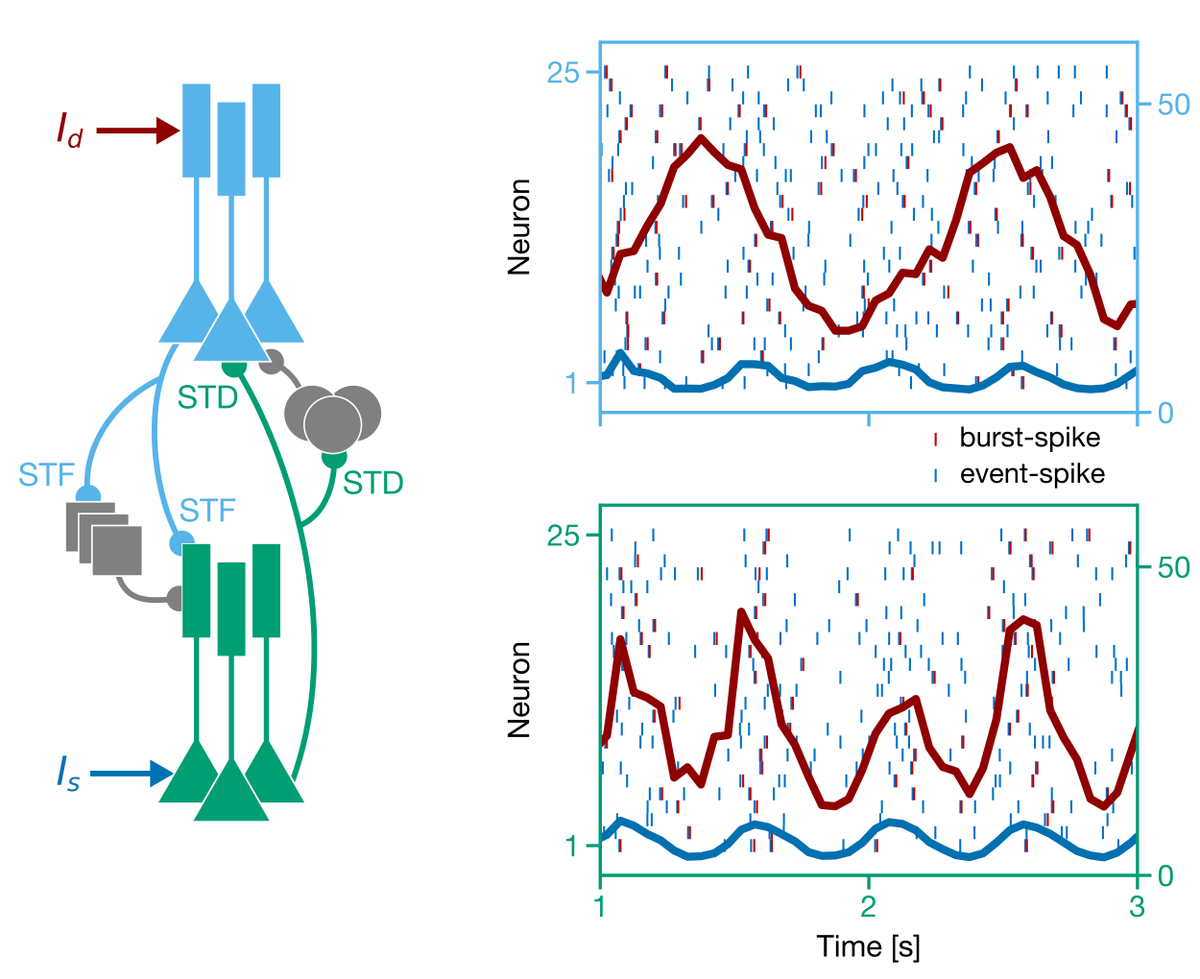
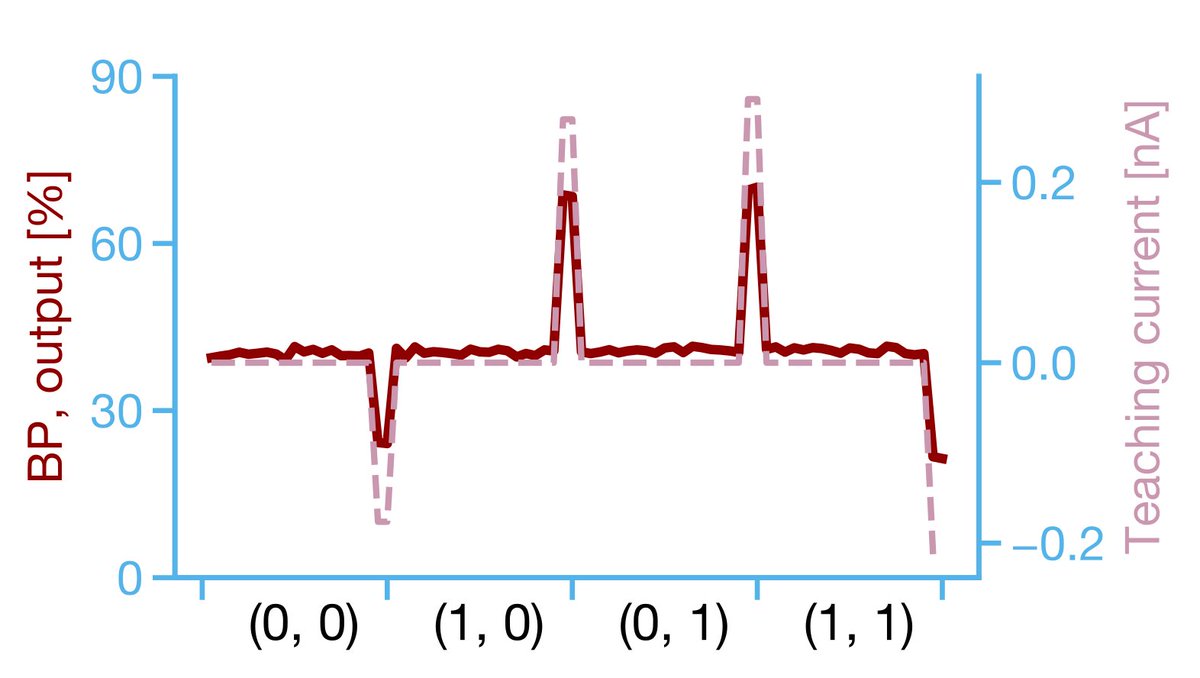
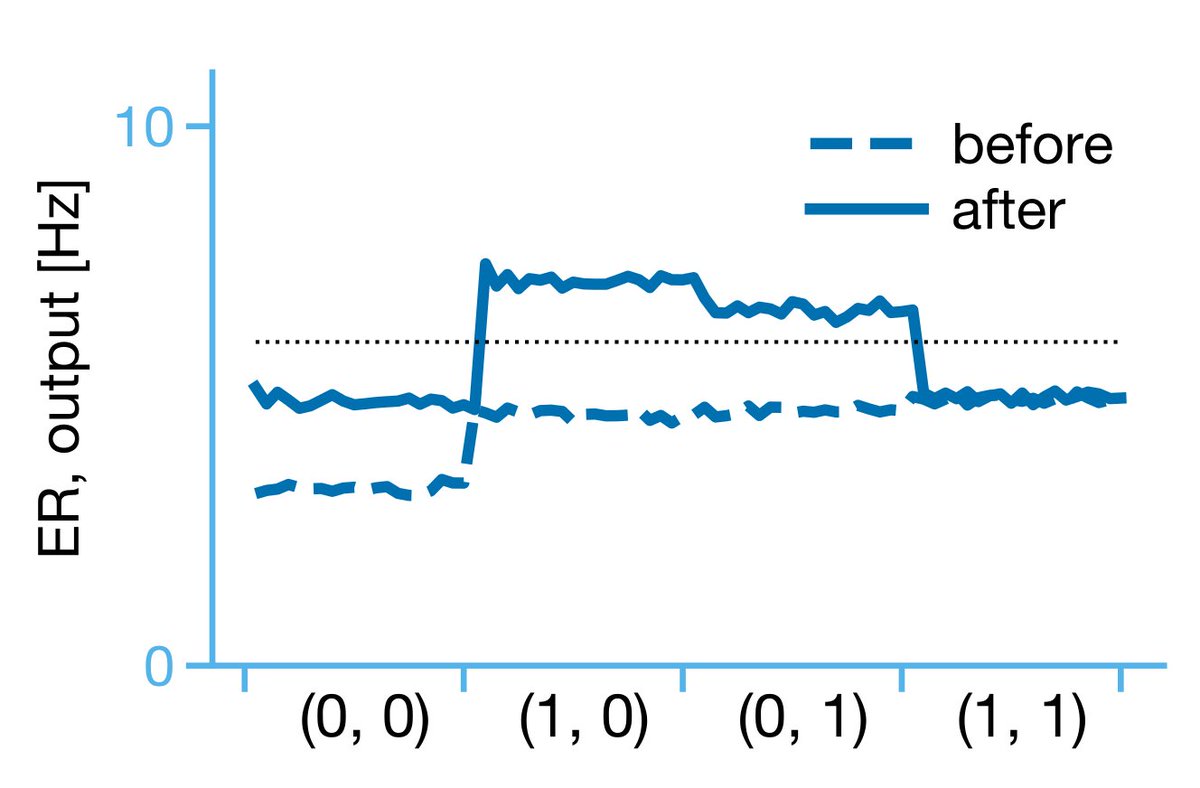
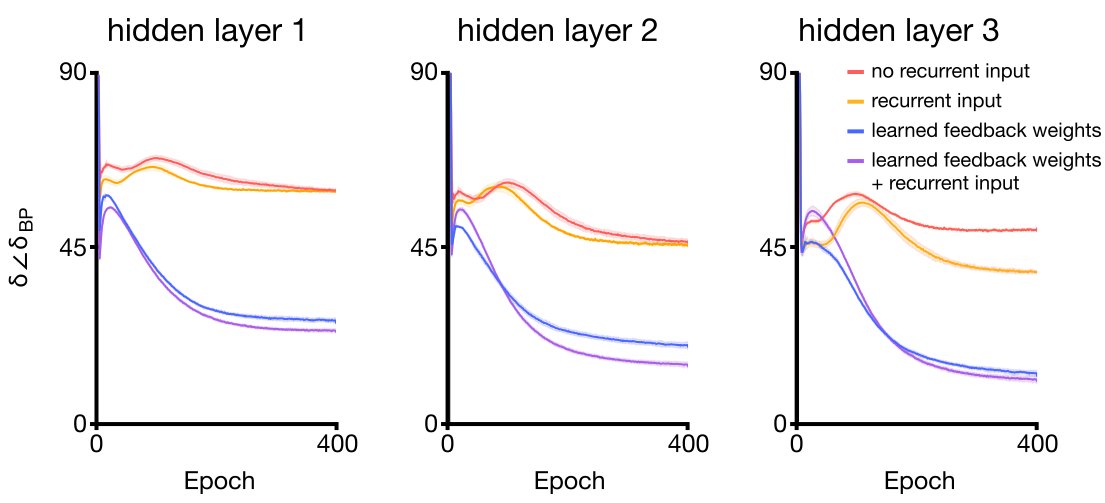
- postsynaptic burst = LTP
- postsynaptic single spike = LTD

4/ First, we asked, what happens when you hook up two neurons in a biophysical simulation with BDSP altering the synapses?

5/ Interestingly, if you run a standard STDP plasticity experiment on a biophysical simulation using BDSP, then you get frequency-dependent STDP, as reported by @pj_sjostrom several years ago (sciencedirect.com/science/articl…).

6/ Another interesting result: if you generate Poisson distributed spiking you get something that is very close to the BCM learning rule (scholarpedia.org/article/BCM_th…).

7/ Moreover, if you combine BDSP with the fact that bursts are generated by coincident apical and basal inputs in pyramidal neurons (e.g. nature.com/articles/18686), then the inputs to the apical dendrites become a teaching signal, telling a neuron whether to engage in LTP or LTD.

8/ Now, this teaching signal role for the apical inputs is particularly intriguing given the capability for ensembles of pyramidal neurons to engage in burst multiplexing (previously discovered by @NeuroNaud and @sprekeler, see here: pnas.org/content/115/27…).

9/ Essentially, if you assume that feedforward (FF) and feedback (FB) pathways (and their corresponding inhibitory circuits) arrive at distinct dendrites and have distinct short-term synaptic plasticity (basal and depressing for FF, apical and facilitating for FB), then...

10/ ...the rate of "events" (which can be either a single spike or a burst) communicates FF info, while the probability of an event being a burst communicates FB info. As such, in a hierarchy of cells, FF and FB signals are multiplexed, i.e. communicated simultaneously.

11/ Combining multiplexing with the role of the apical inputs as a teaching signal for the BDSP rule, you get that a teaching signal sent to the apical dendrites at the top of a hierarchy of pyramidal neurons instruct neurons throughout the hierarchy!

12/ So, for example, we built a biophysical simulation where we arranged pyramidal neurons (with inhibitory motifs) into a hierarchy with two distinct input ensembles, one output ensemble, and a pair of "hidden layer" ensembles.

13/ We then injected current into the somatic compartments of the input units in a standard boolean pattern [(0,0),(1,0),(0,1),(1,1)], and at specific times in the simulation, injected current into the apical dendrites of the output population corresponding to an XOR output:

14/ The result? Over time the hierarchy learned to compute XOR! More specifically, the event rate of the output ensemble gave us the desired non-linear function (higher output to (1,0) or (0,1)). Note, this was dependent on the hidden layer learning.

15/ These results show that BDSP paired with burst multiplexing permits hierarchical credit assignment in biological networks. Very cool! But, we wanted to understand how good this credit was. How does it compare to, for example, gradient information?

16/ We asked: what does the BDSP rule do when we take the limit of infinite ensemble size?

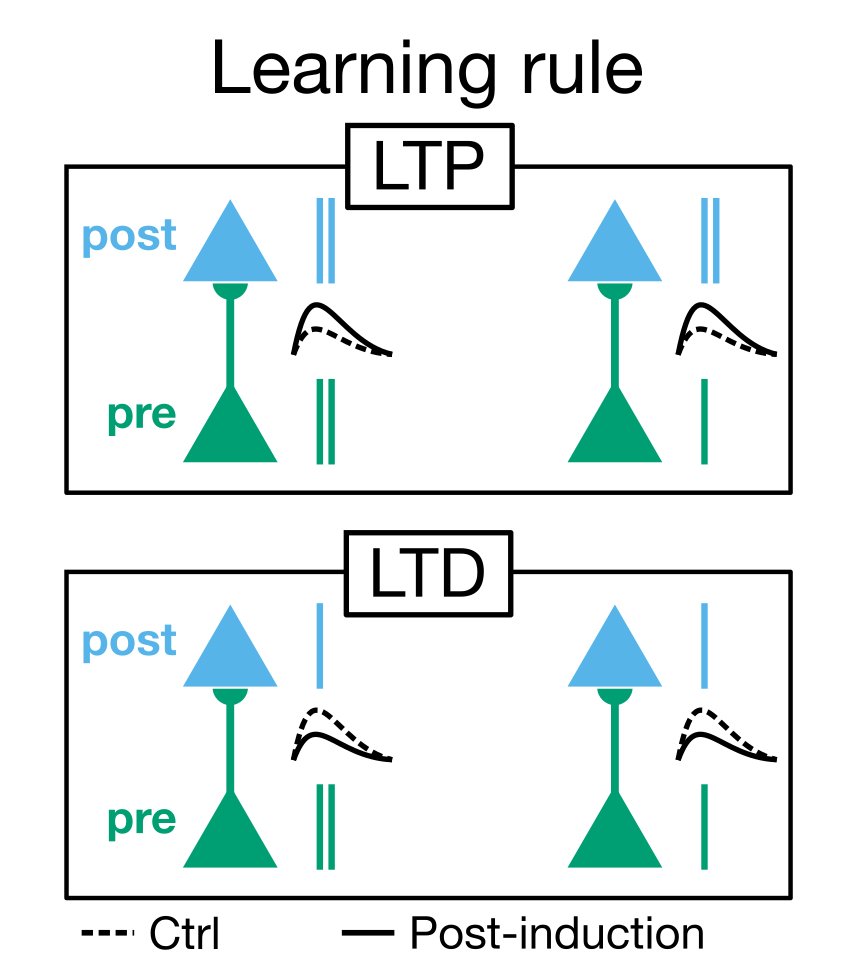
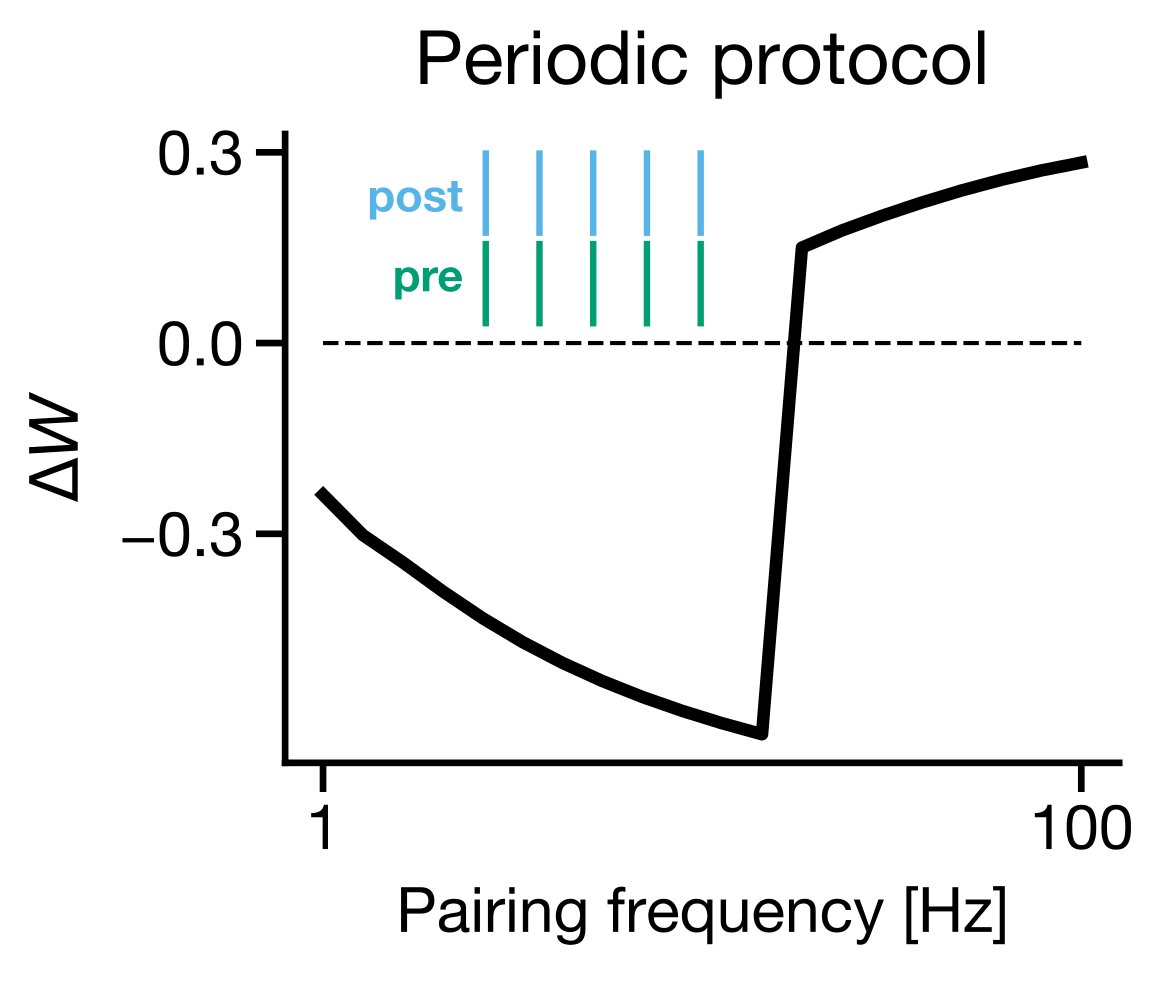
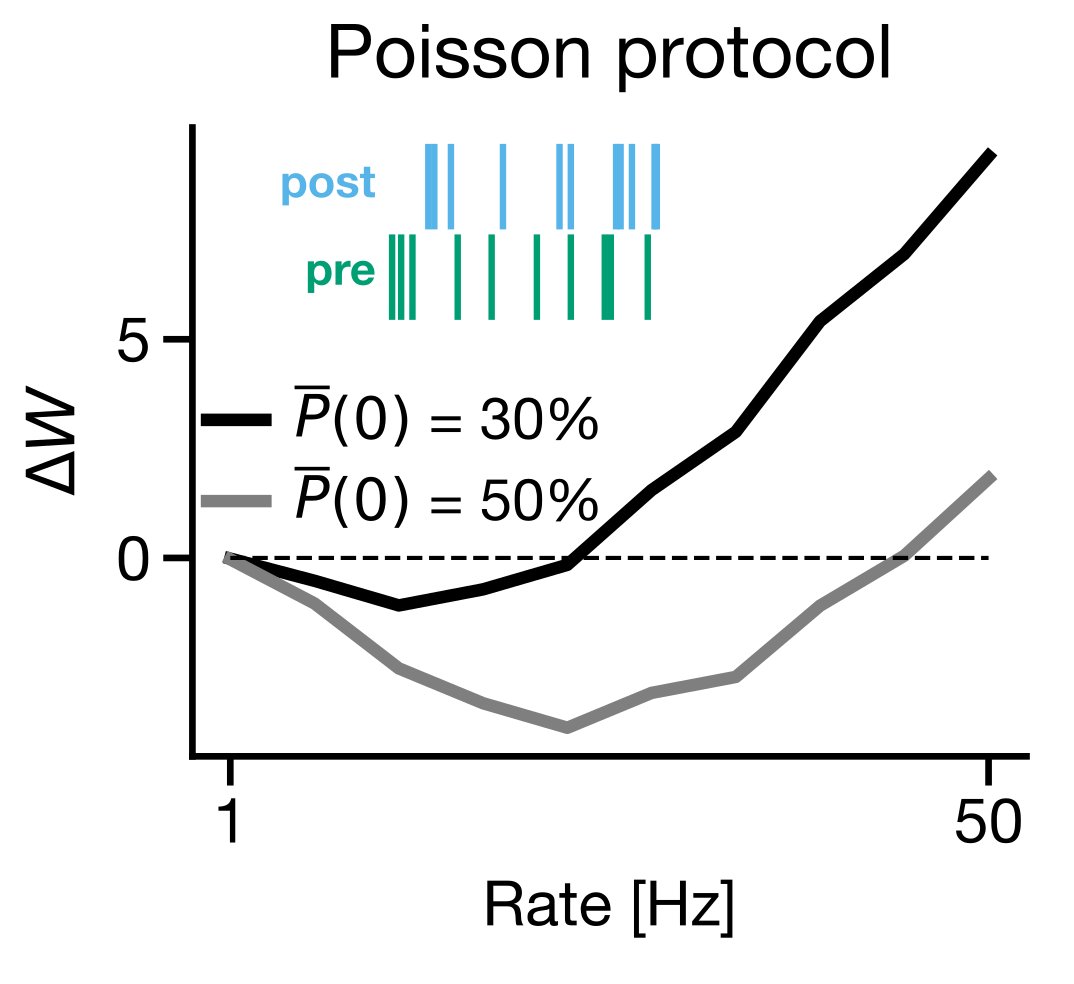
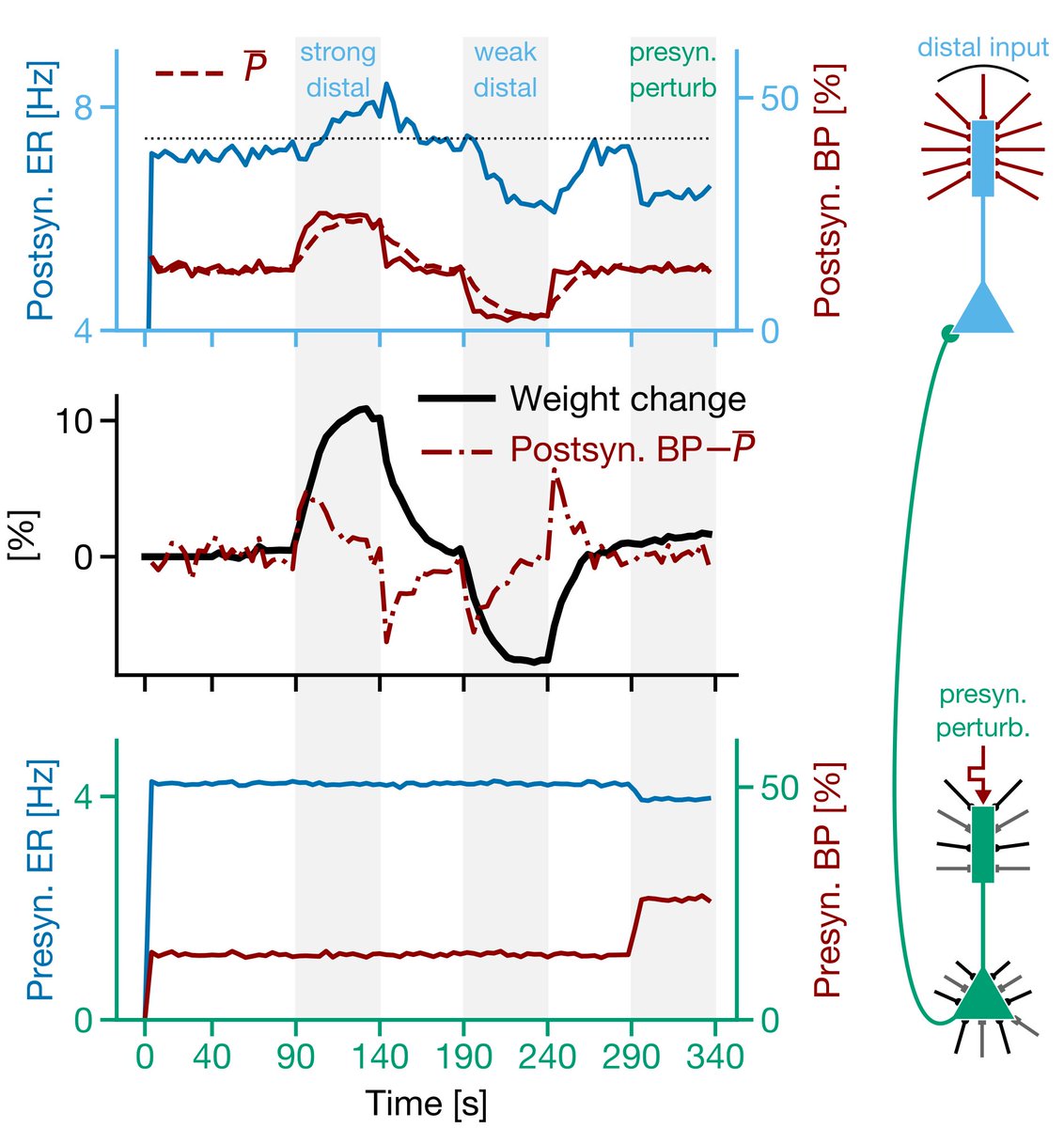
Turns out, if two conditions are met:

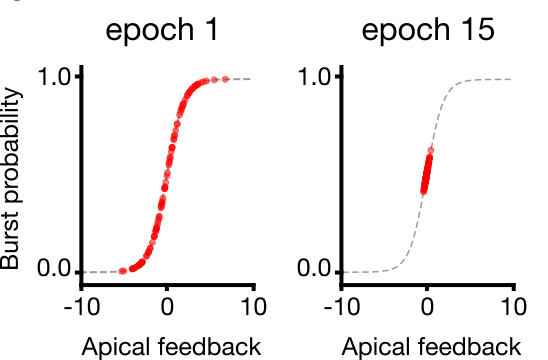
1) Burst probs are a linear function of apical inputs

2) FB synapses are symmetric to FF synapses

Then BDSP in the inf limit is gradient descent!

17/ To model this, we adopted an "ensemble-level" model, where each unit represents a group of pyramidal neurons with three key signals across the ensemble: an event rate, a burst prob, and a burst rate, with the events propagated FF and the bursts propagated FB.

18/ We also added in recurrent inhibition targeting the apical dendrites to the mix. With a homeostatic plasticity rule on this recurrent inhibitory input, we could keep the burst probabilities in a linear regime.

19/ Added to this, we used the fact that burst information is propagated through the entire hierarchy to implement the Kolen-Pollack algorithm on the FB synapses. This allowed us to train the FB pathways to be symmetric with the FF pathways.

See e.g.: arxiv.org/abs/1904.05391

20/ With these two additional plasticity mechanisms, BDSP provides a decent estimator of the gradient. For example, here you can see the angle between BDSP updates and the true gradient across a hierarchy while training on MNIST:

21/ What does this mean for learning performance? To test this, we created a deep network of our ensemble units with conv layers and trained it with the BDSP rule:

22/ Previously, it has been found that other algorithms designed for bio plausibility, such as feedback alignment and difference target propagation, fare poorly on more complicated image classification datasets, including CIFAR-10 and ImageNet (see: papers.nips.cc/paper/8148-ass…).

23/ But, with homeostatic inhibition, and the FB learning, BDSP delivers backprop level performance on CIFAR-10. Note: it beats feedback alignment by a wide margin, and is *way* better than learning with a global reinforcement term (node perturbation). Gradients matter!

24/ On ImageNet, BDSP doesn't reach backprop level performance, but unlike feedback alignment, it actually can learn.

25/ So, the take-away messages are these:

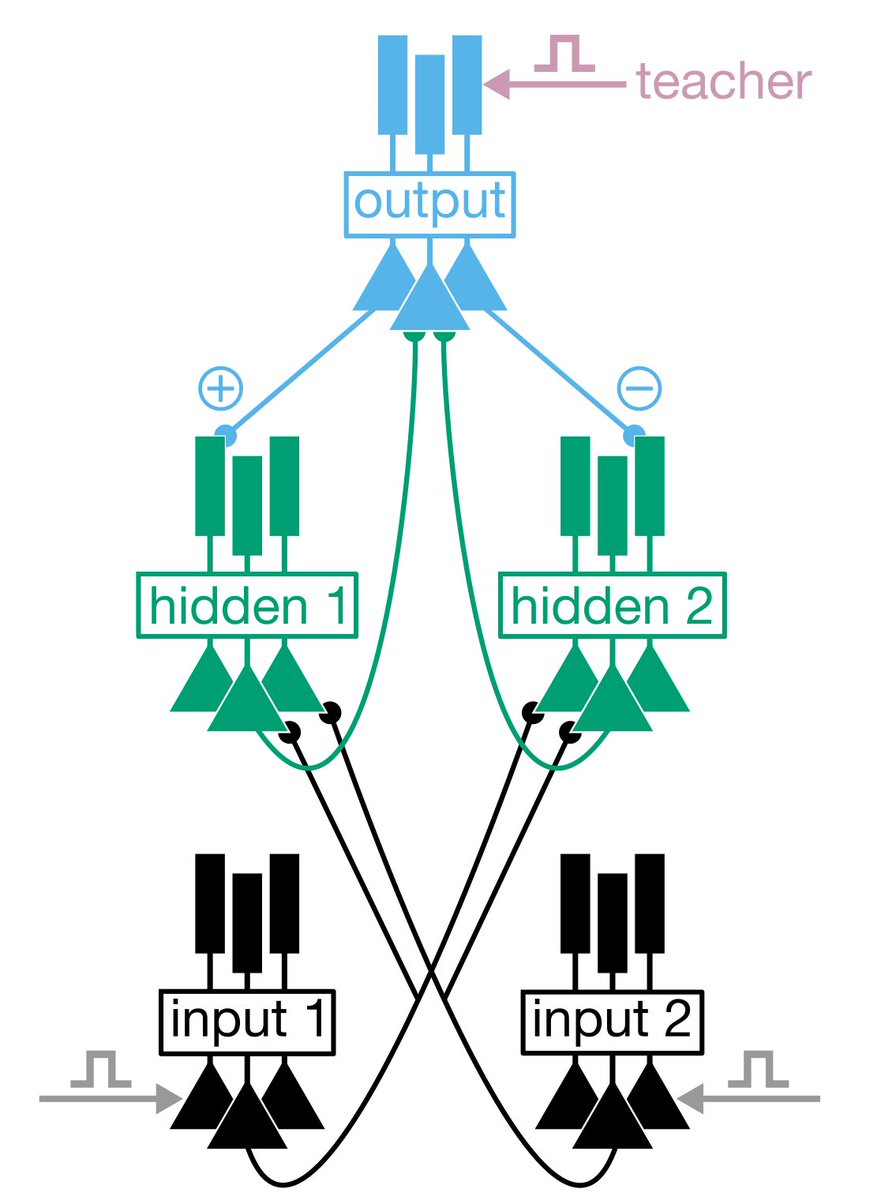
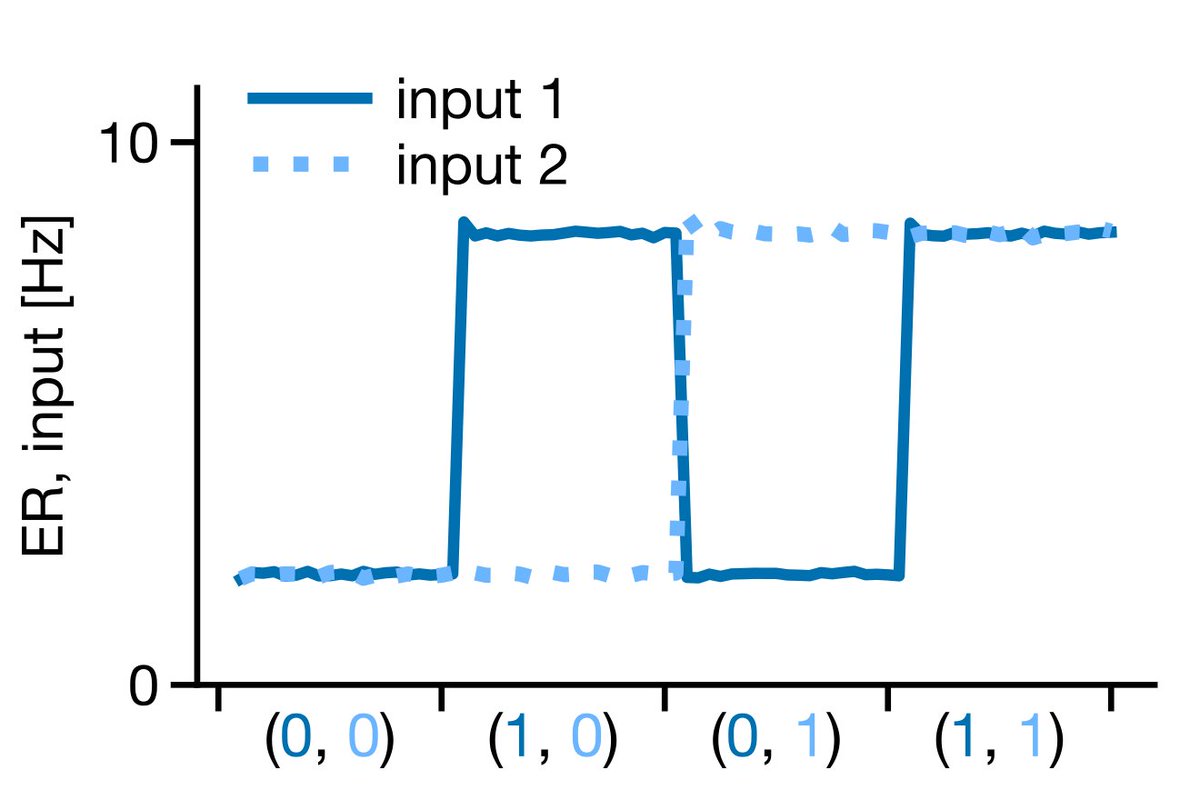
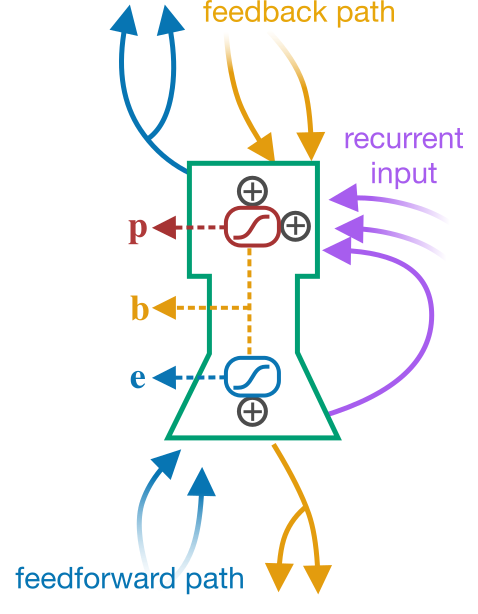
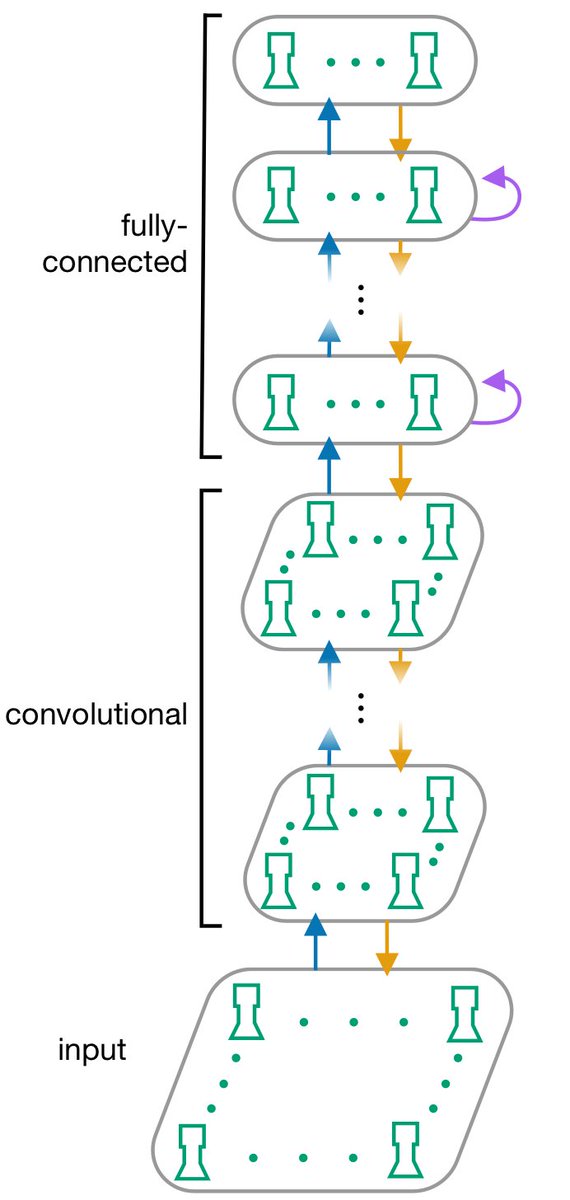
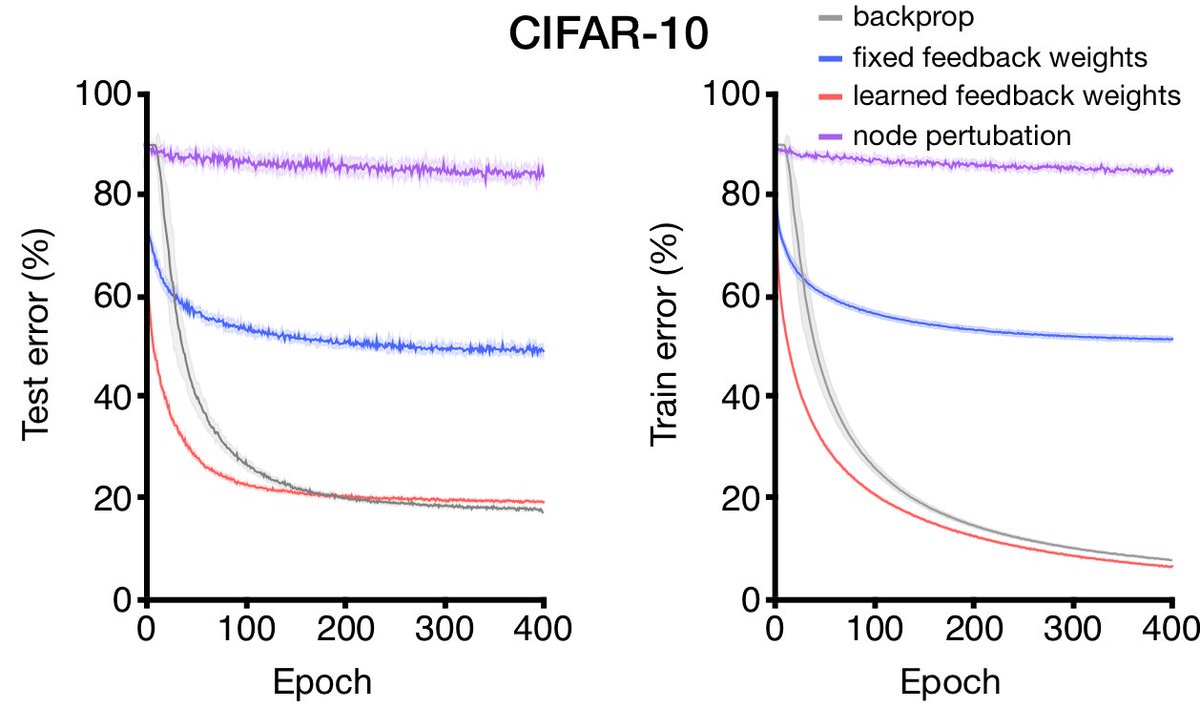
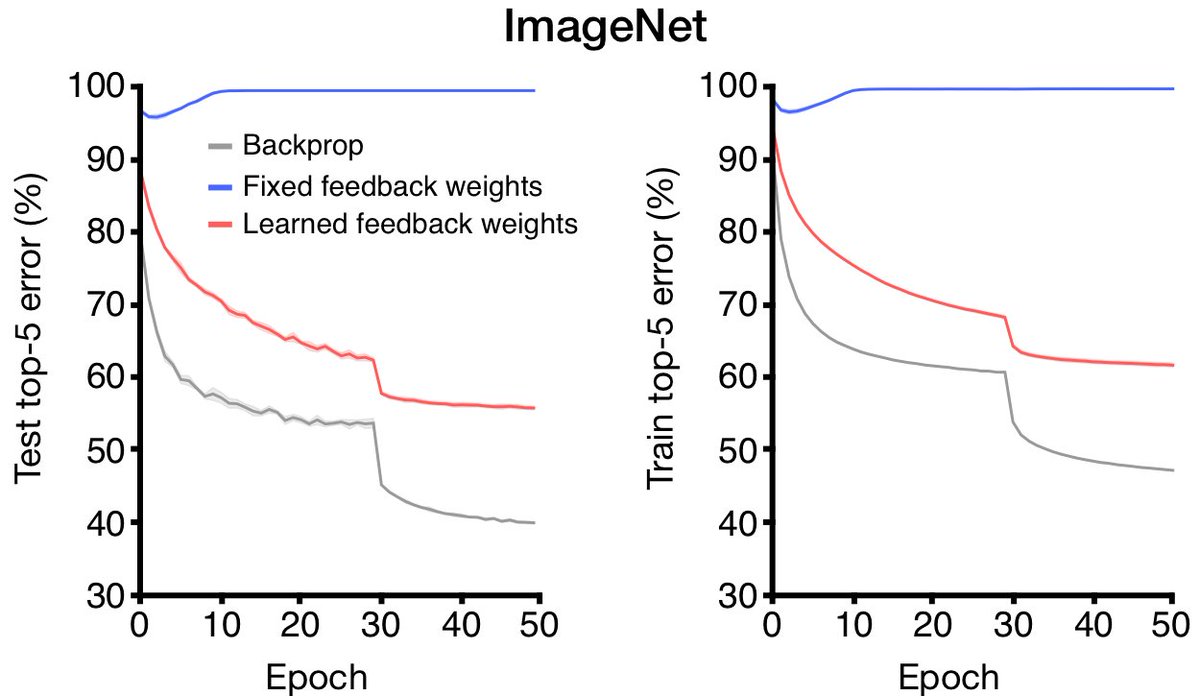
1) We propose a learning rule motivated by biology (BDSP) that can explain previous experimental findings and replicate other comp neuro algs.

2) When you combine BDSP with the unique properties of apical dendrites, and make some assumptions about short-term plasticity in FF and FB pathways, BDSP provides hierarchical credit assignment, all using known biophysical mechanisms.

3) When we examine the behaviour of BDSP in the infinite limit of ensemble size, and add in some additional homeostatic plasticity and FB learning, we get an algorithm that provides pretty good gradient info, and which can learn on difficult datasets.

4) These results demonstrate that well-known properties of dendrites, synapses, and synaptic plasticity are sufficient to enable sophisticated learning in hierarchical circuits.

26/ To cap this massive thread off, I just want to recognize the work we built on here. This really is, in my opinion, the final realization of @KordingLab's vision from long ago. See here: link.springer.com/article/10.102…

27/ It was also directly inspired by the insights from the model developed by Walter Senn, Yoshua Bengion, @somnirons, and Joao Sacramento:

papers.nips.cc/paper/8089-den…

28/ As the final note, this model makes many testable experimental predictions, and if we achieve anything here, it would ideally be to motivate some hypothesis driven experimental science!

29/ Read the paper for some of the specific predictions, but in addition to the basic BDSP rule, there are predictions about short-term plasticity in FF and FB circuits, and predictions about how bursts relate to errors during learning.

30/ If you're still here at the end of this thread, thanks for reading it, and we hope you enjoy the paper!!!

Stay healthy and safe out there!!!

Oh, one last thing for those really into this: you can see my most recent talk on this work at the Oxford Neurotheory Seminar Series (thanks @TPVogels!) on YouTube, here: