Thread by @juliomulero

De repente, estaba encerrado entre paredes de hormigón. Había cientos de presos escribiendo números, uno detrás de otro. Pronto descubrí que perseguían al INFINITO.

¡EL ÚLTIMO NÚMERO!

[[A las ilustraciones... la gran @GabiMartinArte]]

#EnHebrasMatemáticas

Dentro HILO ⬇️

Serían las 18:00 horas de la tarde. Tras la última clase, fui a mi despacho y escuché a alguien en el pasillo. La puerta se abrió. Sólo vi humo.

Lo siguiente que recuerdo: el techo gris y las grises paredes de una habitación sin ventanas.

Me vistieron con una túnica blanca y me entregaron un lápiz. No se te ocurra romperlo; el lápiz, y tú, pertenecéis al Último Número, eso me dijeron. Me agarraron del brazo y me llevaron a la enorme sala contigua donde presos de todas las edades escribían encadenados a las mesas.

Todos estaban escribiendo sin cesar en libros plagados de números correlativos. Un número, otro, otro.

Me sentaron en un pupitre, me encadenaron brazos y pies, y me exhortaron: ¡Escribe! ¡Escribe! ¡ESCRIBE! Y no gastes más papel de la cuenta.

25443, 25444, 25445…

Cada cierto tiempo se escuchaba una voz que retumbaba en las paredes: El #ÚltimoNúmero agradece vuestra entrega y os espera, impaciente, en el Incontable.

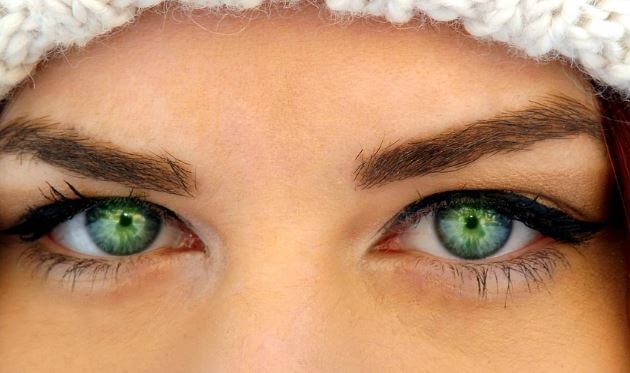
Todo estaba plagado por este símbolo… ¡un infinito truncado! Pero, qué narices…

25446, 25447, 25448…

¡Me habían secuestrado unos locos que estaban buscando el último número! ¡el último número!, y después un lugar al que llamaban el “Incontable”. ¡Qué locura!

25449, 25450, 25451…

Los que estaban allí sentados, levantaron la cabeza y me agujerearon con sus miradas. Los niños y niñas tenían caras extrañas, deformadas; los presos de avanzada edad eran prácticamente una sombra.

Estaban consumiéndose.

25449, 25450, 25451…

Estaba muy agobiado. Estaba condenado. No había salida. La respiración se me aceleró e intenté desencadenarme. No pude. Lo intenté más y más fuerte.

Y, de forma inconsciente, empecé a chillar:

¿ES QUE NO SABÉIS QUE LOS NÚMEROS SON INFINITOS? ¡VAMOS A MORIR TODOOOOS!

Entonces, todo se volvió negro y empecé a sentir que caía… Abrí los ojos y desperté en mi cama, sudando y susurrando “los números son… infinitos, infinit, inf”.

Tardé unos minutos en recobrar la calma y convencerme de que sólo había sido una horrible pesadilla.

Sentí la inexorable necesidad de navegar por la vibrante historia del #infinito, como quien disfruta de una serena calma después de la tempestad más horrible, como quien desea un bálsamo eterno.

Aquí comienza un sueño: el palpitante viaje hacia LO #INFINITO.

Todo surgió cuando el ser humano empezó a reflexionar sobre su mundo:

¿Fue todo fruto de un instante concreto o existió desde “siempre”? ¿Continuará existiendo para siempre o todo colapsará en algún momento? ¿Qué pasaría si viajáramos sin parar en una dirección particular?

O en una versión más “terrenal”: ¿qué sucede si algo se divide en dos trozos, luego se divide de nuevo uno de los trozos y se continúa dividiendo indefinidamente? ¿Podría uno hacer esto para siempre?

¿Se puede repetir algo infinitamente?

Según #Pitágoras, “todo es número” (números naturales). Aparecieron después los #atomistas que creían en los indivisibles (algo así como los átomos) y, finalmente, emergieron los que, como #Zenón, afirmaban que las dos perspectivas anteriores provocaban contradicciones.

Imagínate que #Aquiles se enfrenta, en una carrera, a una tortuga a la que concede cierta ventaja. Cuando #Aquiles echa a correr desde el punto A, la tortuga ya está en el punto B; cuando alcanza ese punto B, la otra ya ha llegado al punto C; y así sucesivamente.

La conclusión era entonces que #Aquiles nunca ganaría a la tortuga, porque tendría que recorrer un número infinito de tramos finitos, algo imposible de hacer en un intervalo de tiempo finito. #Zenón concluía entonces que "el movimiento no existe". De cajón.

Total, nada.

#Aristóteles, contrario a la existencia del #infinito “real”, consideró un #infinito potencial (en potencia) que podía ser obtenido sin manejar en ningún momento el infinito en su totalidad, que aparece como posibilidad y se va construyendo progresivamente.

El #infinito potencial de #Aristóteles sobrevivió (a la derecha de Dios) durante siglos, y convivió con señores feudales, caballeros y renacentistas.

G. #Bruno predicó un universo formado por infinitos mundos y lo pagó en la hoguera.

#Galileo procuró ser muy cauteloso...

Durante el siglo XVII, las matemáticas aceptaban el uso del infinito potencial.

Por ejemplo, en Inglaterra, las series infinitasfueron un tema recurrente y el hecho de que algunas resultaran en un número finito tranquilizaba las mentes de los matemáticos más susceptibles.

El símbolo ∞, por cierto, no es más que una curva matemática llamada lemniscata, y fue usado por primera vez por John #Wallis, en 1655, para denotar el infinito.

#Wallis consideró que el dibujo de la lemniscata encarnaba la idea del infinito a la perfección.

#Newton y #Leibniz desarrollaron, no sin cierto temor, el cálculo infinitesimal, es decir, las matemáticas de lo infinitamente pequeño.

Algunos, como el Obispo de Berkeley, ridiculizaron los infinitésimos “que tan pronto valen cero como toman el valor que al autor le interesa”.

La fundamentación del cálculo fue un hito para las matemáticas, pero el uso de los infinitésimos con la idea de límites, tan necesaria en el cálculo diferencial, necesitó más de un siglo para ser aceptado completamente.

A finales del siglo XIX, existía una escuela constructivista que negaba la existencia de cualquier cosa que no pudiera ser construida a partir de los números naturales en un número finito de pasos. Según #Kronecker, "Dios creó los números naturales; el resto es obra del hombre".

Entonces emergió la figura un matemático que fue capaz de enfrentarse a sus (las) creencias más profundas, y despejó, no sin sufrimiento, cualquier duda que pudiera existir acerca de la "existencia del infinito".

Se llamaba GEORG #CANTOR.

#Cantor (1845-1918) nació en San Petersburgo en el seno de una familia profundamente religiosa.

A sus 11 años, la familia se trasladó a Alemania y su padre, inquisitivo y más interesado en el dinero que en la propia felicidad de su hijo, le obligó a estudiar ingeniería.

#Cantor (1845-1918) nació en San Petersburgo en el seno de una familia profundamente religiosa.

A sus 11 años, la familia se trasladó a Alemania y su padre, inquisitivo y más interesado en el dinero que en la propia felicidad de su hijo, le obligó a estudiar ingeniería.

En la Universidad de Berlín, sus profesores #Weiertrass, #Hermite y, sobre todo, #Kronecker (¡Kronecker!), lo consideraron un buen alumno, pero nada más allá.

Hasta los 22 años nadie habría imaginado que llegaría a ser uno de los más grandes matemáticos de la historia.

A los 27 años, ya como catedrático de la Universidad de Halle, dio inicio a sus principales investigaciones. Para él, "la esencia de las matemáticas descansa por completo en la libertad".

Así comenzó a desarrollar su gran TEORÍA DE CONJUNTOS.

De hecho, dado que #Cantor era un amante de las preguntas difíciles, que el infinito requería una fundamentación y que los #conjuntos (que habían sido tratados intuitivamente) eran los objetos matemáticos que podían merecer dicho adjetivo, era más que razonable empezar por ahí.

Lógicamente, la clave residía en su número de elementos.

Según #Cantor, un #conjunto es “una colección en un todo de determinados y distintos objetos de nuestra percepción o nuestro pensamiento, llamados los elementos del conjunto”.

Dos conjuntos tienen el mismo número de elementos, la misma #cardinalidad o son #equipotentes, si existe una función biyectiva entre ellos, es decir, una función que establece una correspondencia biunívoca entre los elementos de ambos conjuntos.

Todos aprendemos a contar usando una correspondencia (biyectiva) con los dedos de nuestras manos.

#Cantor demostró, usando la función f(n)=2n, que existe la misma cantidad de números naturales que de números pares.

Es así. Curiosamente, y contra todo pronóstico.

De la misma manera, Cantor concluyó que existe la misma cantidad de números naturales que números enteros e, incluso, racionales (las archiconocidas fracciones).

En el fondo, para que esto ocurra, se trata de ser capaces de establecer un primer racional, un segundo, etcétera.

Cuando #Cantor se recuperó del hachazo, llegó la pregunta natural:

¿Tienen todos los conjuntos infinitos el mismo tamaño o puede haber conjuntos infinitos más grandes que otros?

Aquí saltó el bombazo que hizo trizas el resto de su vida.

#Cantor empezó a profundizar en los números reales.

Es importante recordar que no todos los números reales son racionales, pensemos, por ejemplo, en π (3.141596…) que no se puede escribir como una fracción.

Georg #Cantor se sorprendió al comprobar que era imposible establecer una función biyectiva entre los números reales y los números naturales, es decir, ¡hay un infinito más grande que otro!

Más aún... llegó a la conclusión de que hay ¡infinitos infinitos!

(De)mostró que hay infinitos conjuntos de diferentes tamaños.

(De)mostró que, dado cualquier conjunto infinito, siempre se puede hacer uno más grande.

(De)mostró, en fin, la existencia de una secuencia infinita de tamaños infinitos (a los que llamó #transfinitos).

Lo sé. Todo esto es desconcertante. Y así mismo se sintieron los contemporáneos de #Cantor, entre ellos algunas de las mejores mentes matemáticas del siglo XIX.

De hecho, su antiguo profesor #Kronecker llegó a llamarle “renegado, charlatán, corruptor de la juventud estudiosa”.

#Cantor consiguió "domar" al monstruo y, de paso, descubrió que no venía solo.

La oposición de los colegas y sus creencias religiosas no se lo pusieron fácil, aunque algunos como #Dedekind siempre estuvieron de su parte.

Su convicción era profunda, pero había una cuestión muy delicada...

Si ℵ₀ denota el cardinal de los números naturales (el famoso #alephcero) y ℵ₁, el de los números reales, ¿existe un conjunto con un tamaño mayor que ℵ₀, pero menor que ℵ₁?

Esta pregunta fue conocida como la #HipótesisDelContinuo y, tante ella, #Cantor entró en bucle.

Un día, probaba que sí, al día siguiente, demostraba lo contrario.

Y, sorprendentemente, no estaba equivocado en ningún caso.

Años más tarde, Kurt #Gödel, inspirado por esta pregunta, llegó a la conclusión de que hay afirmaciones matemáticas que no pueden ser probadas ni refutadas.

Y este era el caso de la Hipótesis del Continuo. No se podía decidir acerca de su veracidad, ni acerca de lo contrario.

Le cerraron las puertas de algunas revistas. Rechazaron trabajar junto a él.

"No sé qué predomina en la teoría de #Cantor, si la filosofía o la teología, pero estoy seguro de que lo que no hay ahí es matemáticas", reprochaba su antiguo profesor #Kronecker.

A lo que #Cantor, más comedido, replicaba:

“Yo sabía exactamente el efecto inmediato que esto tendría: que Kronecker se irritaría como si lo hubiera picado un escorpión […]. ¡Parece que realmente logré ese objetivo!".

"La visión [del infinito] que considero la única correcta es compartida por pocos. Aunque, posiblemente, yo sea el primero en la historia en tomar esta posición tan explícitamente, ¡estoy seguro de que no seré el último!".

#Cantor fue un visionario. Y no se equivocaba.

Los episodios de depresión maníaca, la controversia sobre sus matemáticas, y la muerte de su madre, su hermano y su hijo menor provocaron que Georg pasara los últimos años de su vida entre idas y venidas al hospital psiquiátrico de #Halle.

Georg #Cantor murió el 6 de enero de 1918, convencido de que, en cierta manera, era el “Prometeo del infinito”.

A su muerte, los matemáticos comenzaron a reconocer su trabajo. David #Hilbert, quizás el matemático más importante de su tiempo, afirmó que la obra de #Cantor era "el producto más asombroso del pensamiento matemático".

La vida de Georg #Cantor se desarrolló en la fina línea que separa los plácidos sueños de las más horribles pesadillas.

Se enfrentó a una gran pregunta y la resolvió, se enfrentó a sus compañeros y el tiempo colocó a cada uno en su sitio.

Georg #Cantor, luces y sombras, abrió el camino de las matemáticas modernas y así lo vio el que posiblemente fue el último de los grandes matemáticos: David #Hilbert.

Nadie nos expulsará del paraíso que #Cantor ha creado para nosotros.

◼️ David #Hilbert

Porque:

Si el espacio es infinito, estamos en cualquier punto del espacio. Si el tiempo es infinito, estamos en cualquier punto del tiempo.

◼️ Jorge Luis #Borges

Si has llegado hasta el final, muchísimas gracias.

Muchas gracias a @aperezsanz, cuya experimentada aguja afianzó estas humildes puntadas.

Y, sobre todo, muchísimas gracias a @GabiMartinArte, cuyo arte ha ilustrado a la perfección todas estas ideas.

#EnHebrasMatemáticas