Thread by @bencbartlett

What is the P≟NP problem and why would solving it revolutionize the world (and earn you $1M)? A Twitter thread:

Contents:
‣ Turing machines and time complexity
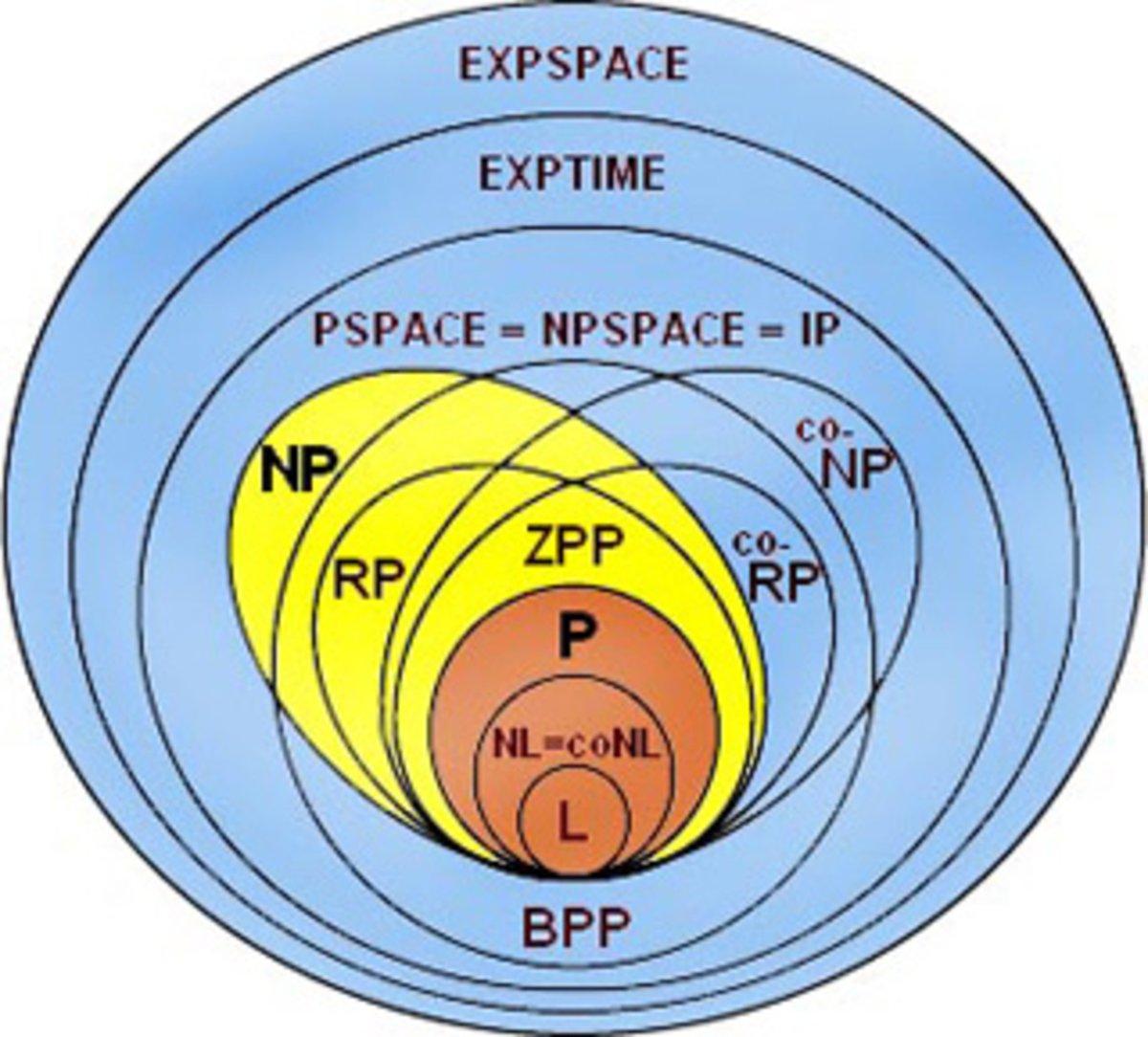
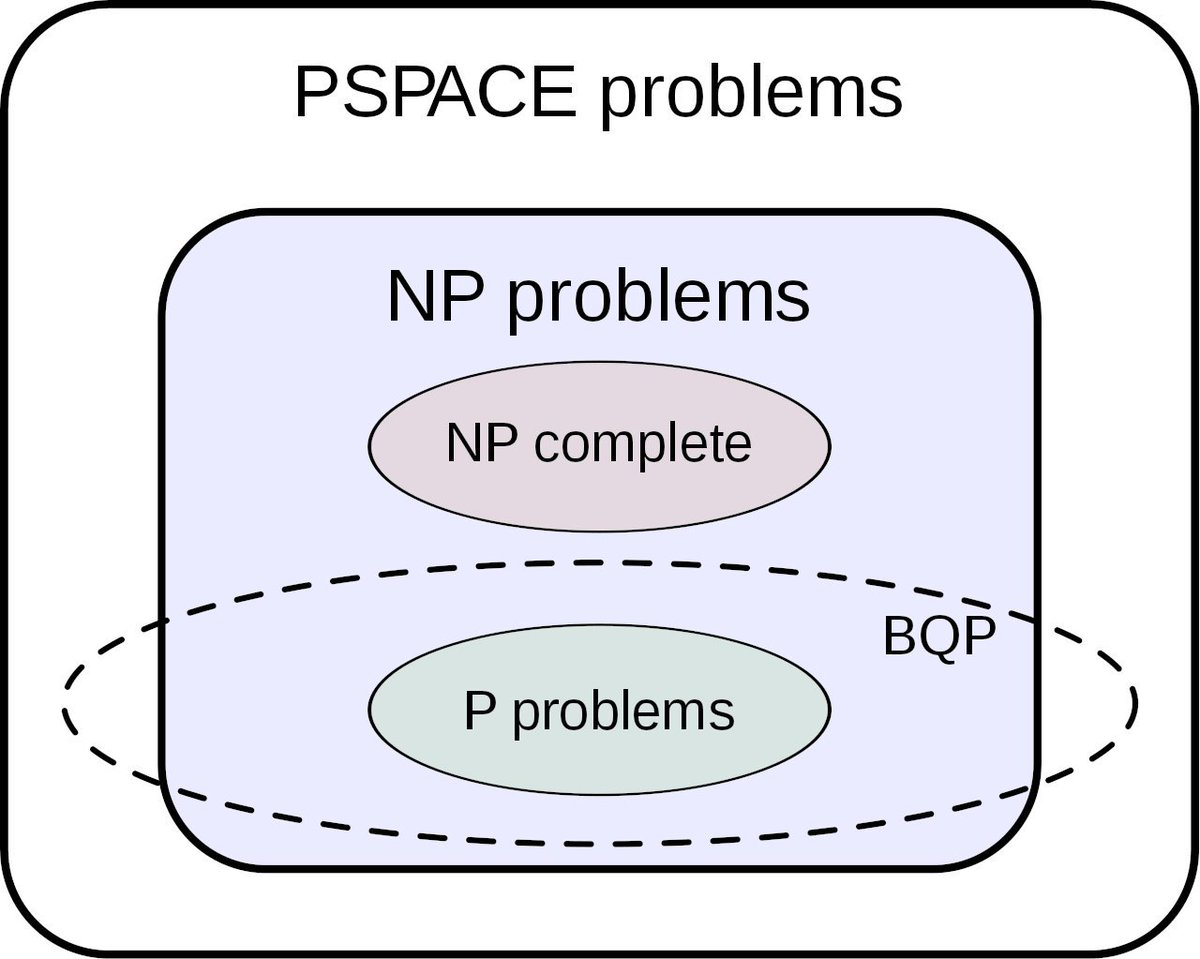
‣ Complexity classes
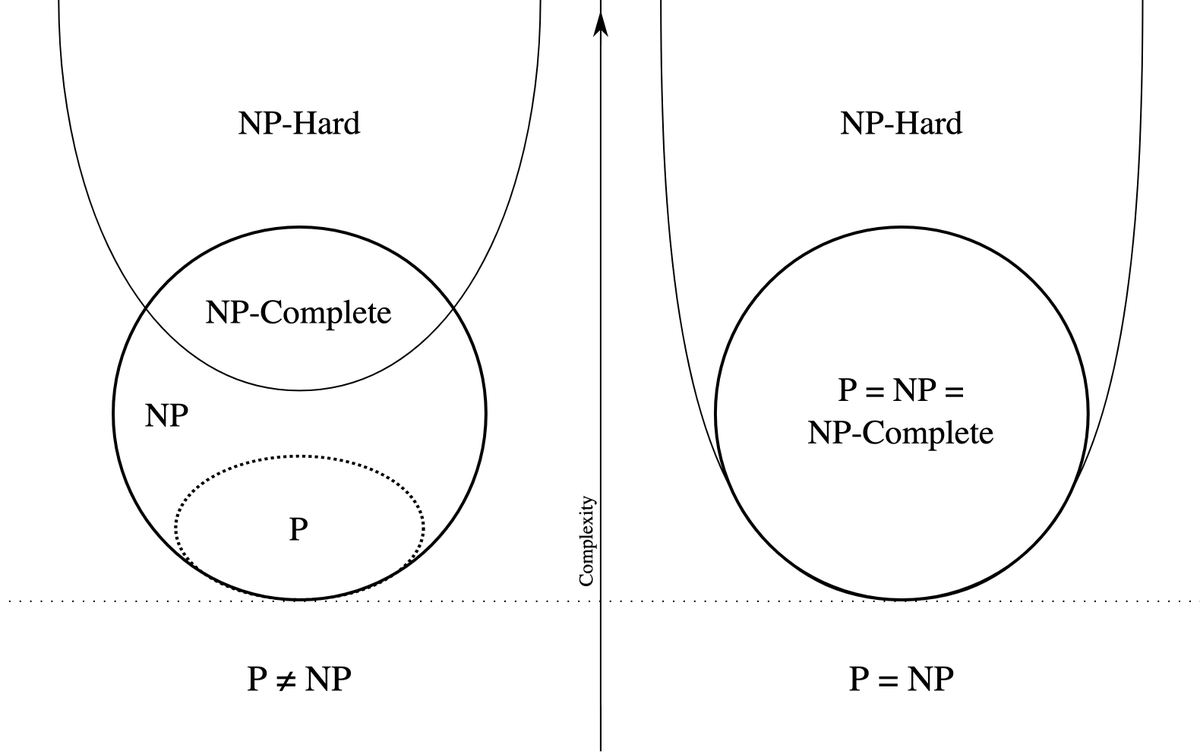
‣ P and NP
‣ Reducibility
‣ Impacts of P=NP
‣ Impacts of P≠NP
‣ Further reading

[1/n]

P≟NP is probably the most important unsolved question in computer science. It asks whether problems which are easy to verify solutions to are also easy to solve.

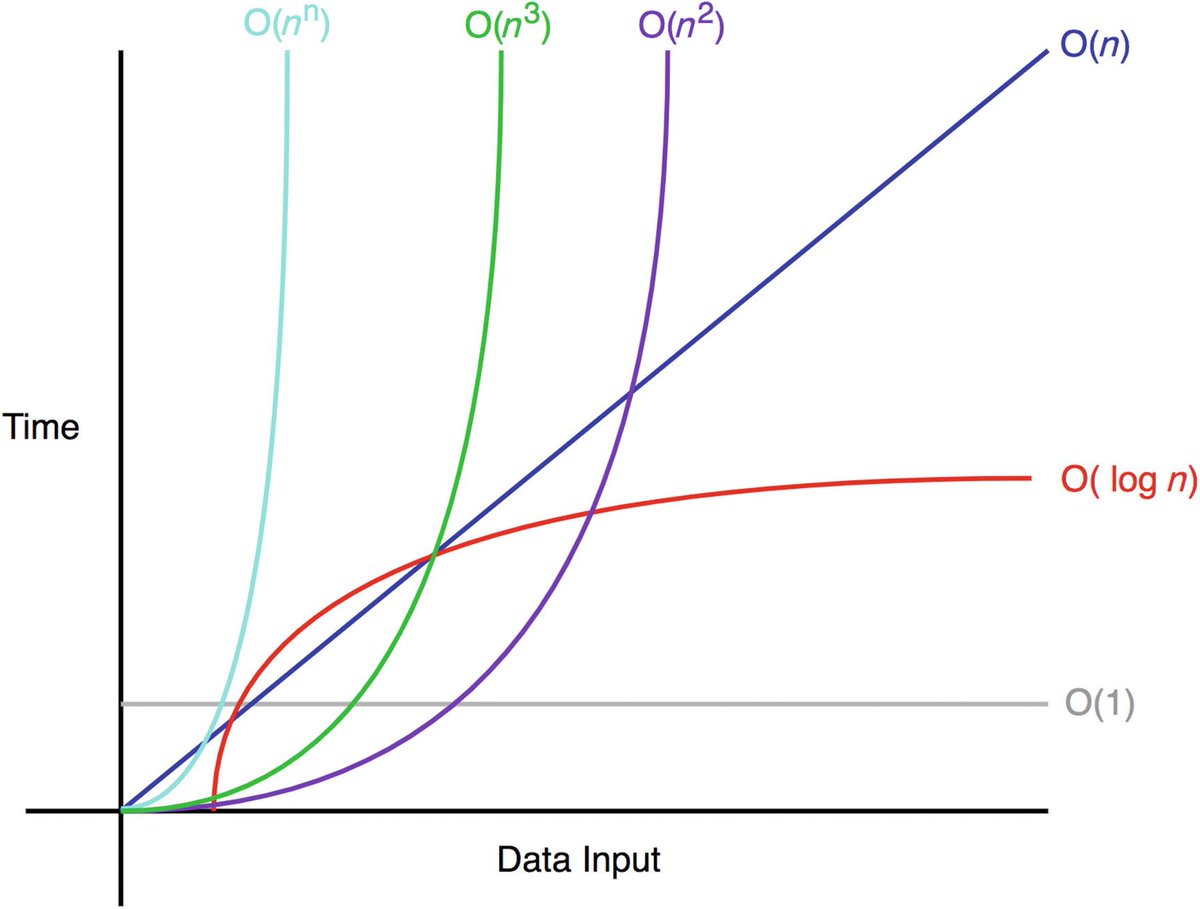
To understand the question and why it is important, let's take a crash course in complexity theory... [2/n]

Complexity theory is a branch of math/CS which classifies problems by how much resources & time they take to solve. The model of computation we typically refer to is a Turing machine, a mathematical generalization of a computer which manipulates symbols on an infinite tape. [3/n]

When thinking about how much time it takes to solve a problem, we often use "big O notation" to describe how the difficulty scales with the size of the input.

For example, consider trying to find a word in a dictionary containing 𝑁 words... [4/n]

If you just check every single word sequentially, then worst case you look at all 𝑁 words, so the complexity is O(𝑁).

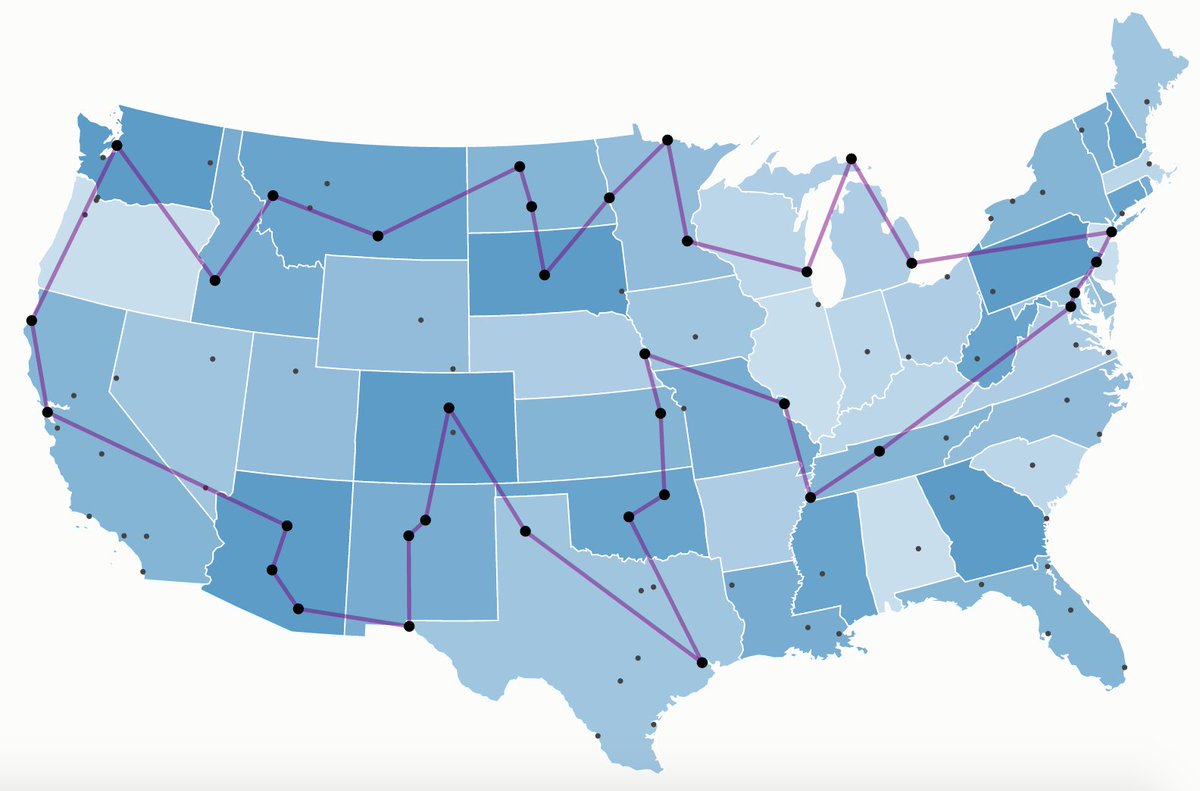
If you instead use a binary search, you cut the number of possible solutions in half with each step, so it only takes O(log₂𝑁) number of steps. [5/n]

Some problems aren't as easy to solve. For example, graph coloring tries to find a way of coloring a graph with 𝑁 vertices using 𝑘 colors such that no two adjacent vertices have the same color. The fastest known algorithms for this run in "exponential time": O(2^𝑁) [6/n]

It is useful to group problems by the amount of time and resources they take to solve using a Turing machine (or other computational model). These groups are called complexity classes, and together they form a "complexity zoo"! [7/n]

There are a lot of complexity classes, but as you might have guessed, two of the most important ones are P and NP.

The P≟NP question asks whether these two sets of problems are actually the same. [8/n]

P is the set of all problems solvable by a Turing machine using a polynomial amount of time, e.g. O(𝑁), O(𝑁²), O(𝑁³ log₂𝑁), etc.

When computer scientists talk about a problem being "easy" or "efficient" to solve, they mean that it is solvable in polynomial time. [9/n]

NP is the set of all problems which can be verified, but not necessarily solved, in polynomial time.

For example, graph coloring is hard to solve, but if I give you a solution, it is easy to look at each vertex and verify that none of its neighbors are the same color. [10/n]

By definition, every problem which is in the set NP is also in the set P: if a problem is easy to solve, it is easy to verify its solutions. So we know that P⊆NP (NP is at least as large as P). [11/n]

However, the other direction - whether NP⊆P - is very much an open question. This is the essence of the P≟NP problem, which asks:

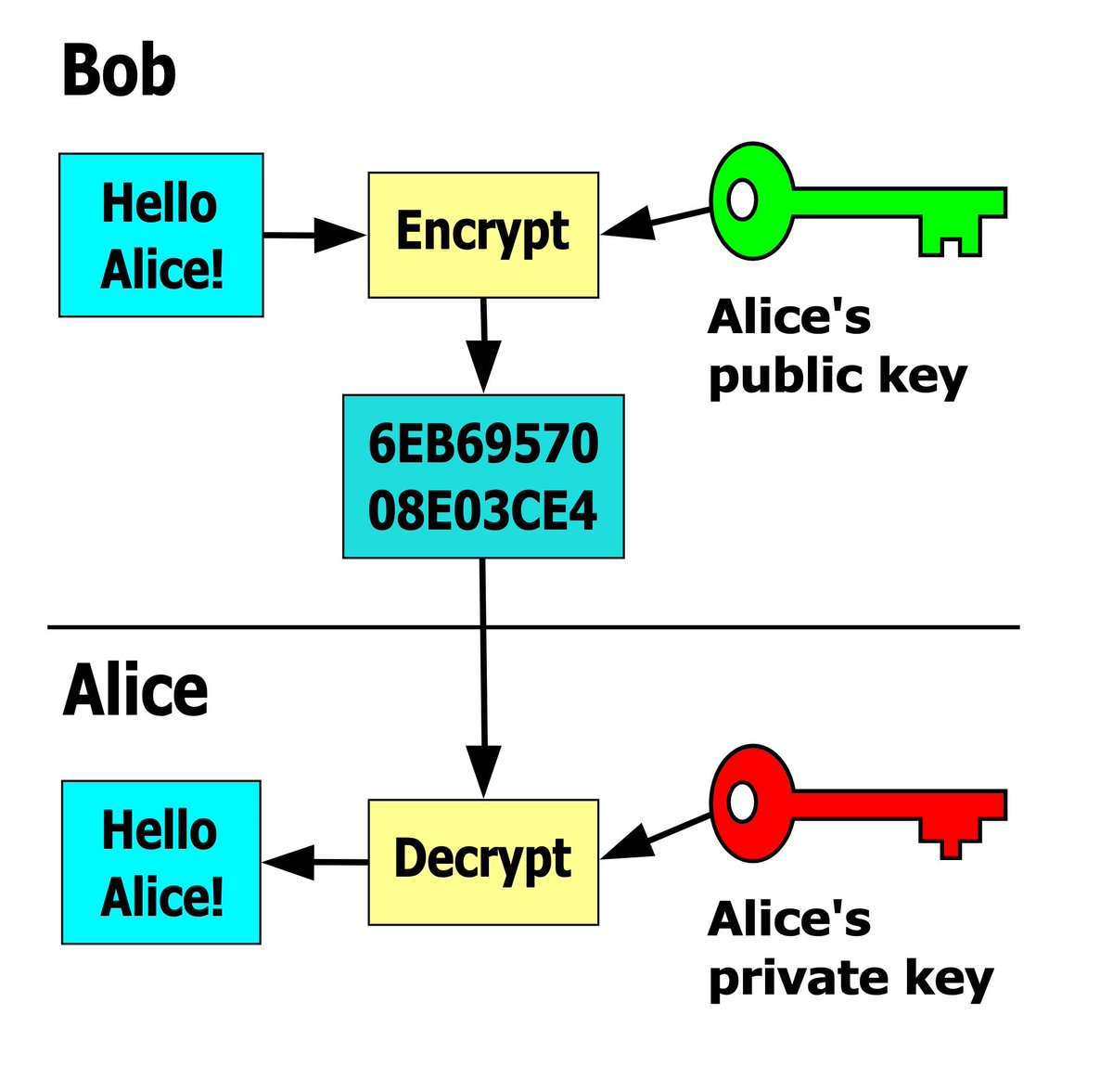
"If it is easy to check that a solution to a problem is correct, is it also easy to solve the problem?" claymath.org/millennium-pro… [12/n]

So why is the problem so important? A constructive proof that P=NP would have truly stunning practical consequences. To understand why, let's talk about reducibility... [13/n]

Algorithms for solving a problem can be used to solve many other problems. For example, you can use an algorithm to solve graph coloring to solve sudoku by constructing an appropriate graph with 81 nodes and using 9 colors! [14/n]

If you can use an algorithm for solving problem A to solve problem B, then B is reducible to A.

There can be some overhead involved in transforming problem A into problem B. If B can be reduced to A using polynomial overhead, we say that it is efficiently reducible. [15/n]

So how does this relate to P≟NP?

The hardest problems in NP are called NP-complete, and this group includes many important problems/applications:
- Graph coloring
- Scheduling
- Internet routing
- Physics + chem simulations
- Drug engineering
- Delivery logistics
[16/n]

Importantly, if you have an NP-complete problem X, you can efficiently reduce any NP problem to X - including all other NP-complete problems!

So if you prove P=NP and find an efficient algorithm for even one NP-complete problem, you can use it to solve *every* NP problem! [17/n]

Proving that P=NP constructively would profoundly change the world, but it would also break the internet! NP problems are perfect for encryption, and almost all modern cryptographic systems operate on the assumption that P≠NP. [18/n]

In public-key cryptography, you want a problem that is hard to solve but easy to verify. In RSA encryption, it is hard to factor a 1024-bit number to get the private key needed to decrypt the message, but easy to verify the decryption given the private+public key. [19/n]

So if P=NP, almost all modern security systems need to be redesigned. P equalling NP would (probably) be even worse for cryptography than quantum computers! Although that's a whole separate thread for another day...

(Un?)fortunately, most scientists believe that P≠NP. [20/n]

Scott Aaronson puts this well: "If P=NP, then the world would be a profoundly different place than we usually assume it to be. There would be no special value in "creative leaps," no fundamental gap between solving a problem and recognizing the solution once it's found... [21/n]

...Everyone who could appreciate a symphony would be Mozart; everyone who could follow a step-by-step argument would be Gauss; everyone who could recognize a good investment strategy would be Warren Buffett." [22/n]

Even if P≠NP, a proof of this would still greatly deepen our understanding of complexity. It would also help us know how powerful quantum computers are! The relationship between BQP (problems easily solvable on a QC) - and other complexity classes isn't well understood. [23/n]

I just hit the Twitter thread limit, so I'll wrap this up 😂

I'm happy to answer any questions people have!

If you want to learn more about complexity, I recommend Chris Umans' notes (users.cms.caltech.edu/~umans/cs21/in…) and Michael Sipser's classic text (amzn.to/32ZGcSB)

[24/24]

An equivalent definition (and where the N comes from) is that NP is the set of problems solvable on a nondeterministic Turing machine in polynomial time. An NTM is basically a Turing machine that can explore every branch of a computation at once.