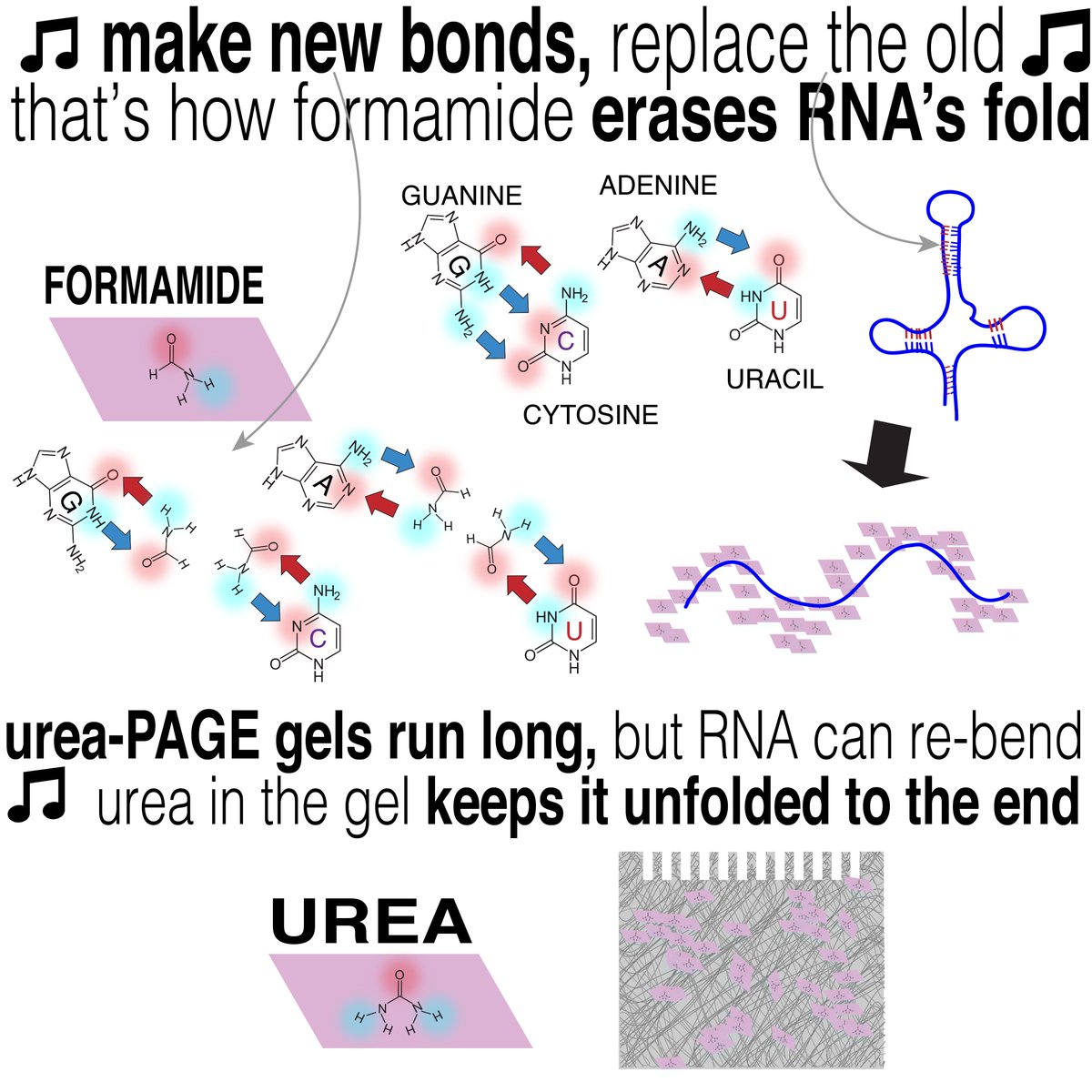
Thus, we can think of rebalancing as selling insurance against the tail risks of an individual manager.
"Virtual rebalancing" is an interesting potential benefit of ensemble approaches.
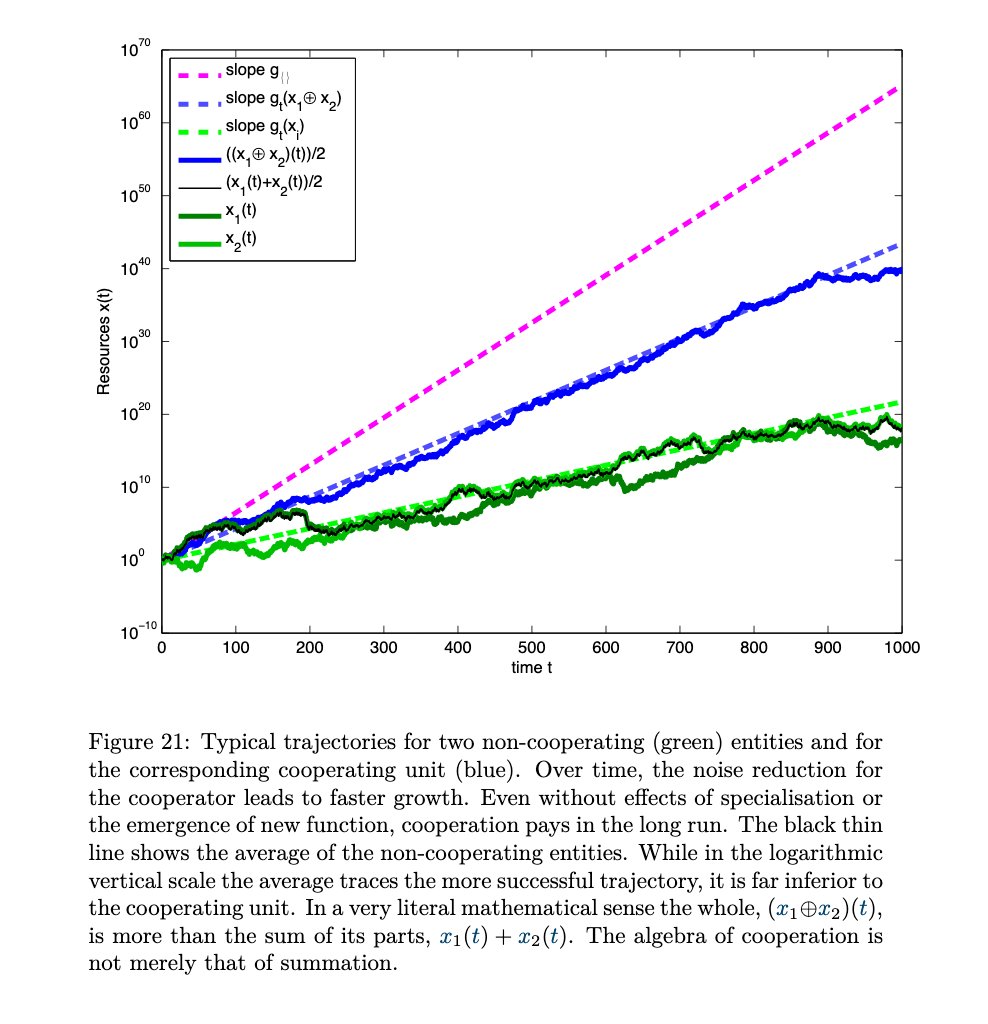
But even if we believe one manager is inferior (e.g. fast trend vs slow trend), the ensemble can still benefit!
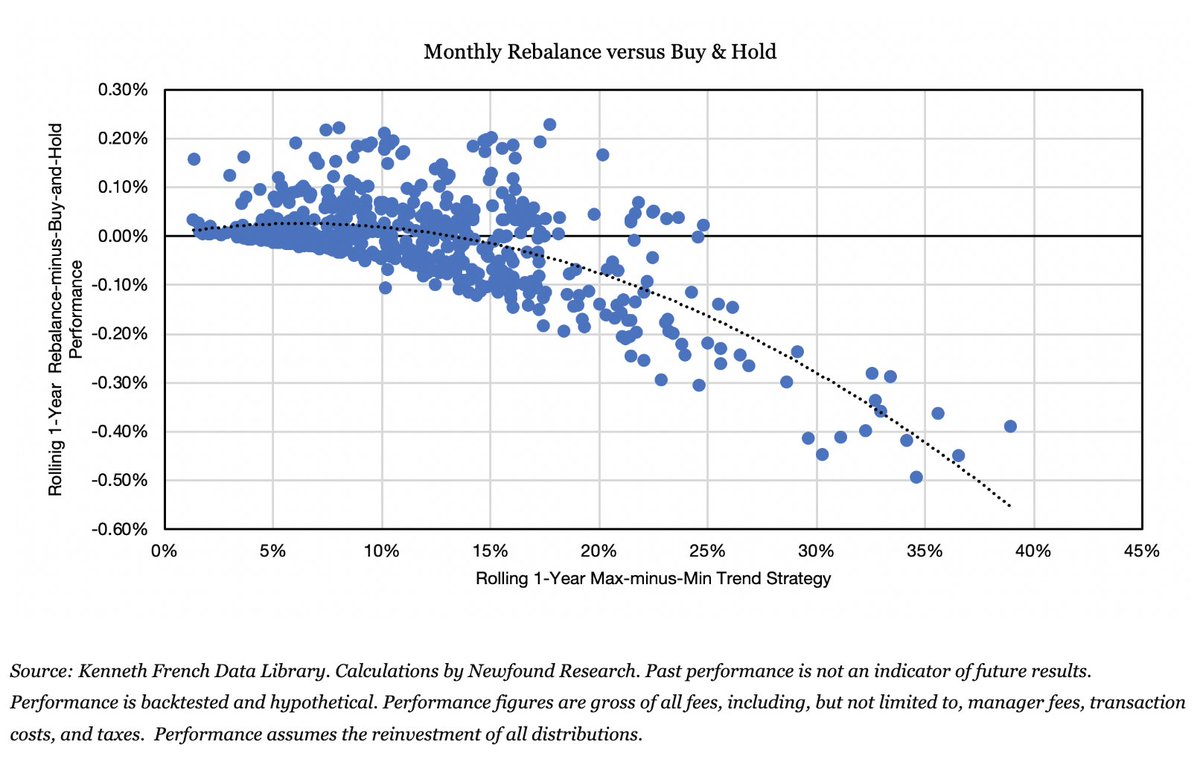
"However, when rebalancing is applied to a set of securities with comparable growth rates, the dispersion discount will be small and hence the volatility return is likely to dominate and generate a positive rebalancing return."
FIN