========================
2nd and final part of the tweetorial, from ORBITA-HQ!
Fun, easy and informative [*]
#MedEd #FOAMed #cardiology #cardiotwitter
[*] Results may vary and are not guaranteed. See small print.
* Some fears are one-and-done:
I get a cold which progresses to pneumonia. Will I die, or recover?
* Other things hang over us for much longer, perhaps all your life.
Will you get hit by a bus?
Get a heart attack?
There's no "sell by" date on the fear.
You are walking through Hyde park, minding your own business.
Hardly causing any trouble at all.
Perhaps the odd humorous tweet.
You get a Direct Message:
"Enough of ur abuse!
You will be hearing form my agent shortly.
kthxbai
AJ Kirtane"
You see the agent:

There is a single arrow.
If it misses, can that particular shot suddenly kill you later that day, or tomorrow?
But you do have a bit of a sweet tooth, and a big tummy.
Your doctor calculates your 10-year CV risk as "15% over 10 years".
You are not very good with numbers, but this doesn't sound good to you.
"Per year, it's only 1.5%! You are 98.5% infarct free this year!"
This slowly sinks in as better news.
"Per day, 0.004%. So stop worrying."
Let's summarise so far.
DO THE EXPERIMENT and
COUNT THE BODIES
The only thing that matters is how many people died (or whatever).
is mathematically best. Frank Harrell has no doubt got a few chapters in his "Baffling Book of foRmulas" [BBR] about why Odds Ratio is preferable.
In short, ODDS ratio lets us see that 90% mortality is much better than 99%, even though the RISK ratio is almost 1.
is easiest for general people to understand.
For probabilities that are much closer to 0 than 1, odds ratio and risk ratio are almost the same. So we can almost interchange them.
But both are for "one and done" things.
Whether you die at 5 am or 9 am, of your pneumonia, is no great difference to your family. There is an answer to "did you survive or not", which is what matters.
================
In the case of dying of life in general, there is no ultimate escape. Eventually it's gonna get you. The only question is when.
So a treatment that makes life safer for you, doesn't change the "final" percentage. Its 100% one way or another.

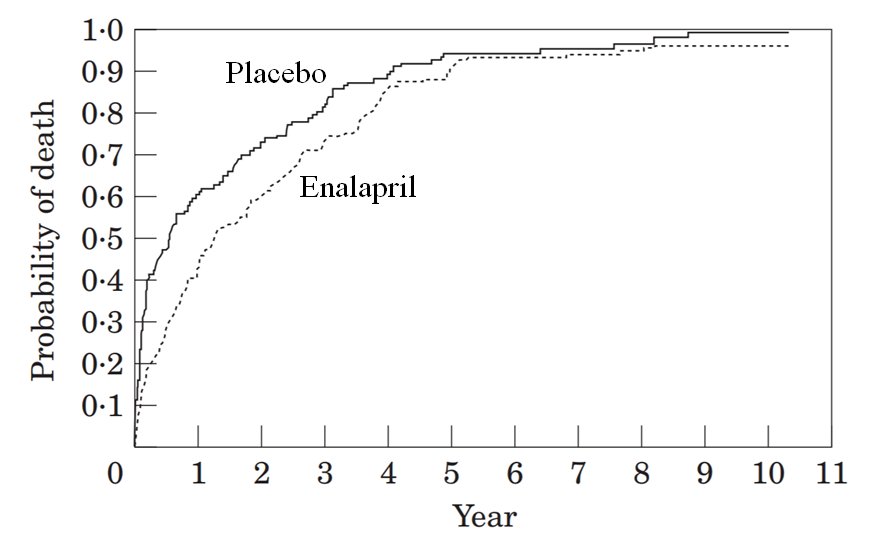
So why are ACEi now routine care in chronic heart failure?
So the relative risk was almost 1.
That's not the way to study the benefit of an intervention in patients who have very severe, lethal disease.
Look carefully at the second year of the trial.
In which arm did MORE ACTUAL PEOPLE die, in the second year?
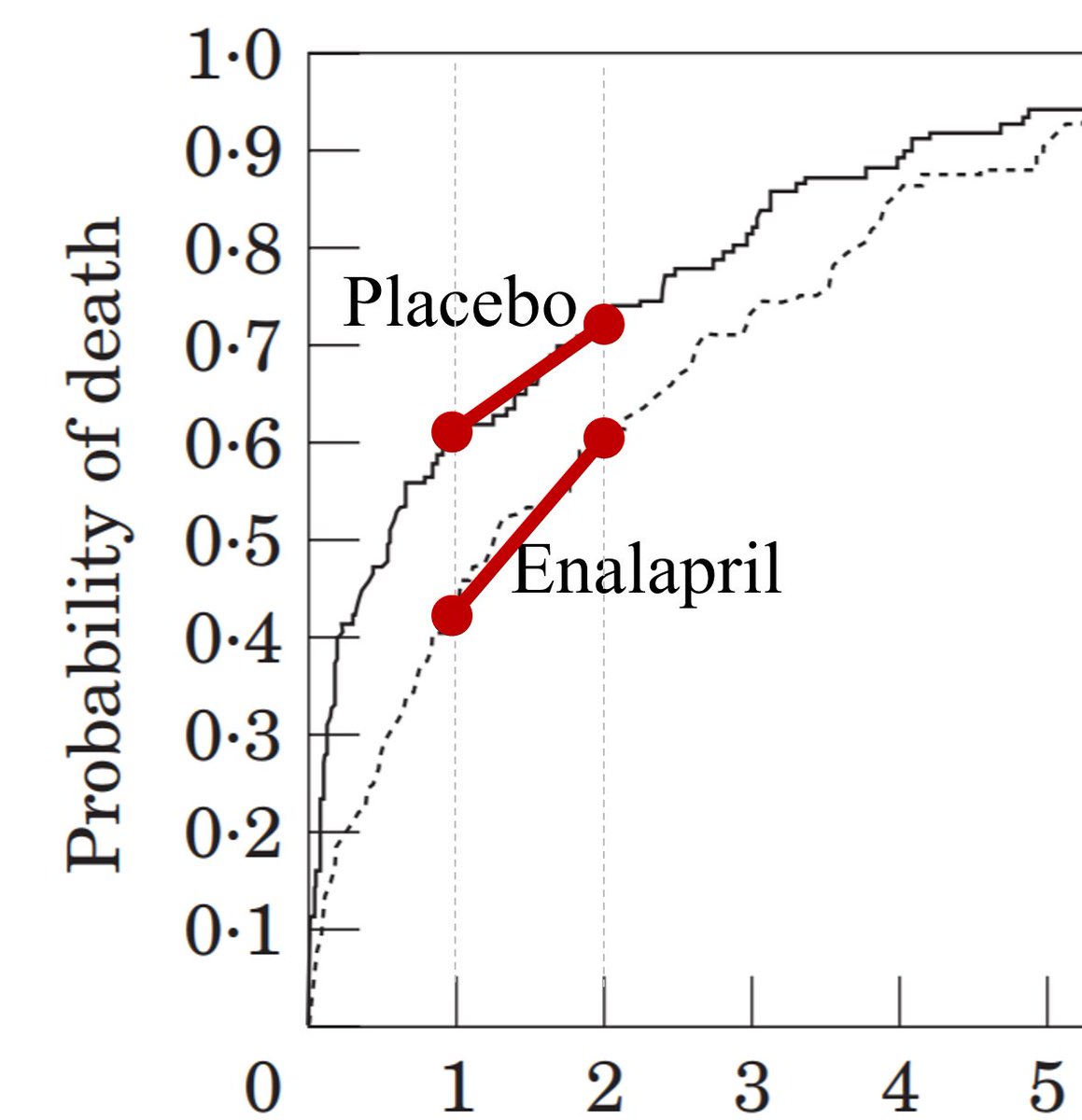
This is almost the same as asking,
"Which red mortality line is steeper?"
We'd have convened a secret committee to tell us to change the Primary Endpt to:
There's a perfectly good reason why there were more deaths in the enalapril arm than the placebo arm, in the second year:

Let's look at a short bit of time in the placebo arm.

The deaths are the red wedge, accumulating steadily through time (even though it is a short time).
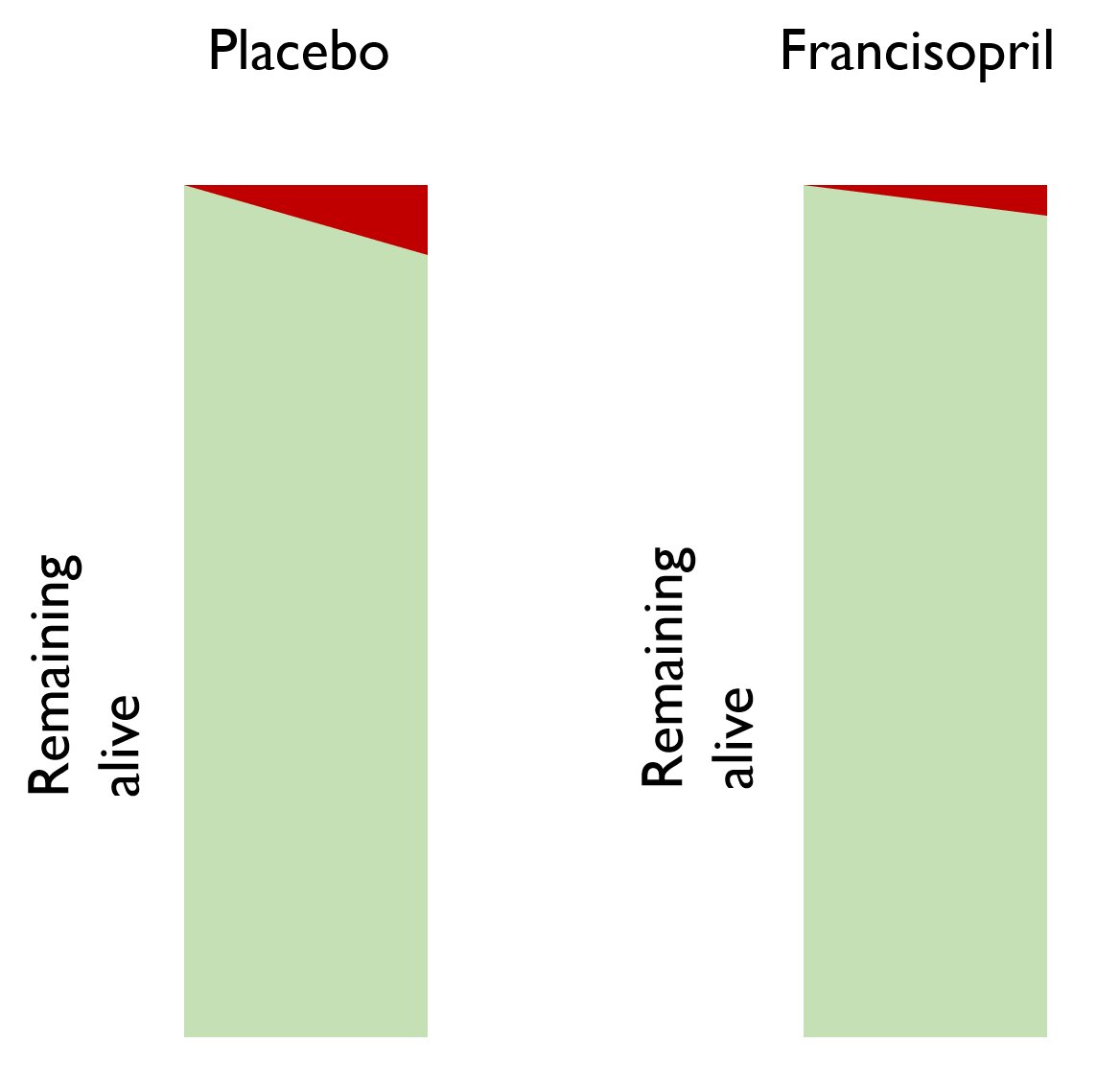
There have been fewer deaths in the francisopril arm.
There are 80 patients in the francisopril arm, but only 40 in the placebo arm.
As you watch for a while, 4 people die in each arm.
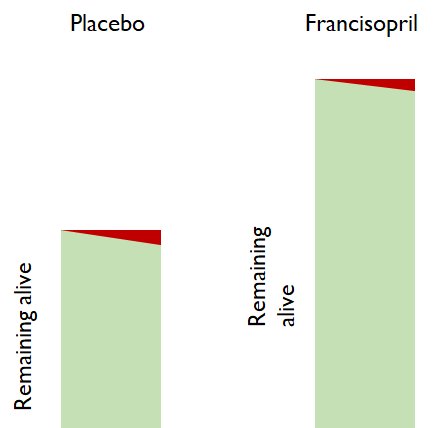
In the active arm 4/80 people died
In the control arm 4/40 people died
Think about it. If you now had a free choice of "active" or "control" treatment, which would you take?
4 people died in each arm.
Which arm was better?
Don't look at "how many people died in that arm, during that time".
Look at "what PROPORTION of the people in that arm at the start of the time, died during that time."
Which arm had a better mortality rate?
If you did NOT pick the majority answer, please click here to be beaten to your senses.
EXPLANATION:
docs.google.com/document/d/1WG…
Hazard Ratios

In each little bit of time, we ask "how risky is it to live through THIS BIT OF TIME in the active arm, compared with being in the placebo arm".
What would you choose, if you are sensibly evaluating the riskiness of each arm?
[A] How MANY people died in the active versus control arms?
[B] What PROPORTION of the people died in the active versus control arms?
You might start with:
Time | Number or ppl alive
| Active Control
0y | 100 100
1y | 90 80
What is the relative risk of the active arm, for that window of time, from 0 to 1 y?
Now let's look at the second year, i.e. from t=1yr, to t=2yr.
Time | Number alive
| Active Control
1y | 90 80
2y | 81 72
What is the relative risk during THIS window of time?
Some of you were just answering "RISK" in the active arm, not "RELATIVE risk"
Step 1. What is the RISK (i.e. proportion of those alive at the beginning of the period, who die during the period) in the active arm?
Step 2. Ditto for control arm.
Step 3. Calculate ratio, active÷control (as always).
docs.google.com/document/d/1Il…
Are they the same or different?
This is because real life is noisy and wiggly.
We don't want to track all those ups and downs: they are mostly noise and don't tell us anything useful.
* which arm was more risky on average?
* by how much?
* could this have easily arisen by chance, or is it more dramatic than normally happens by chance, i.e. statistically significant?
i.e. we want an overall Hazard Ratio, a CI and p value.

It is not guaranteed to be correct, due to me not really understanding how hazard ratios are calculated.
Here is the Cox robot:

"maybe the active arm is 0.9 x the risk in the control arm, at every point in time,
or maybe 0.8 x,
or maybe 1.2 x?
Which fits the data the best?"
It is finding a SINGLE scale factor that relates the risk in the active to that in the control.
Just to be sure you understand what I mean by a single scale factor working across the whole trial, let's do a quick check.
Look at the two event curves in this study below.
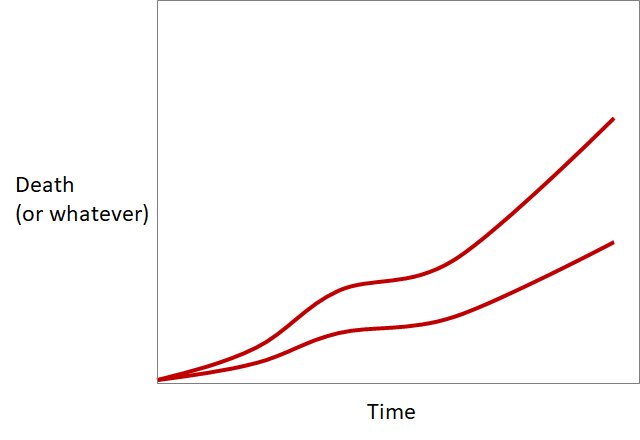
(a single vertical stretching or shrinking manoeuvre)
that can change one red curve into the other?
Do you think there is a single scale factor
(a single vertical stretching or shrinking manoeuvre)
that can change one red curve into the other?
Look at these 2 curves.
"You think you are doing something useful with these idiotic tweetorials?
Well you are not!
How many companies line up to get you to run their trials.
I'll give you a clue: NONE.
You can only do trials ordinary riff-raff are interested in"
And your puzzles are ridiculously easy.
That one you posted this very minute, that people can't solve?
I could do it!
In a second.
So fast it would make your head spin!
Let me show you."
OK, take it away G Onstegger!
It will never be a perfect fit because
Over a very short period of time, Hazard Ratio is is numerically identical to Risk Ratio.
However, over the trial as a whole, Hazard Ratio is weighted in a special way.
For example, at the beginning of the survival graph, there are many patients in it.
Near the end, there are many fewer patients.
The beginning, where there are lots of patients, and so each "%" is made up of many actual people?
Or near the end, where there are few patients, and one death could be worth many %?
The first two votes to the question of "why will the curves not be an exact scaling of each other" are "because each patient is unique"
What on earth are you thinking?
That was a vacuous moronic "Top-People-speak" phrase I put in that NOBODY should pick.
(a) It is true
(b) It is not the explanation for the question at hand and yet
(c) The average audience member thinks it is some sort of deep analysis.
Next time anyone says that to you, throw a rotten tomato at them.
"That tomato was unique too.
Is that relevant?
If it was the same as this tomato [Throw another one]
would it matter?"
That'll teach them.
So the only way for them to be EXACTLY scaled versions of each other, is: EVERY time someone dies in one arm, EXACTLY 2 people die in the other arm at the same moment.
Or similar.
More info on how those steps arise is in this perma-torial:
medpagetoday.com/publichealthpo…

At the beginning, if in a particular month 4% of people die, this might be made up of 40 people out of 1000.
Near the end of the trial, 4% of people dying in a particular month might be made up of 1 person dying out of 25.
The percentage made up of lots of people (4% of 1000, near the beginning of the trial)?
Or the percentage made up of few people (4% of 25, near the end of the trial)?
So during SOME periods of the trial we are more confident about what the hazard ratio is, than we are at other periods.
[*] This is because despite extensive deep research, i.e. reading the wikipedia page a few times, I still can't get the hang of it.
It also gives a confidence interval and P value.
And a therapy (statins) which reduces coronary events by a steady fraction.
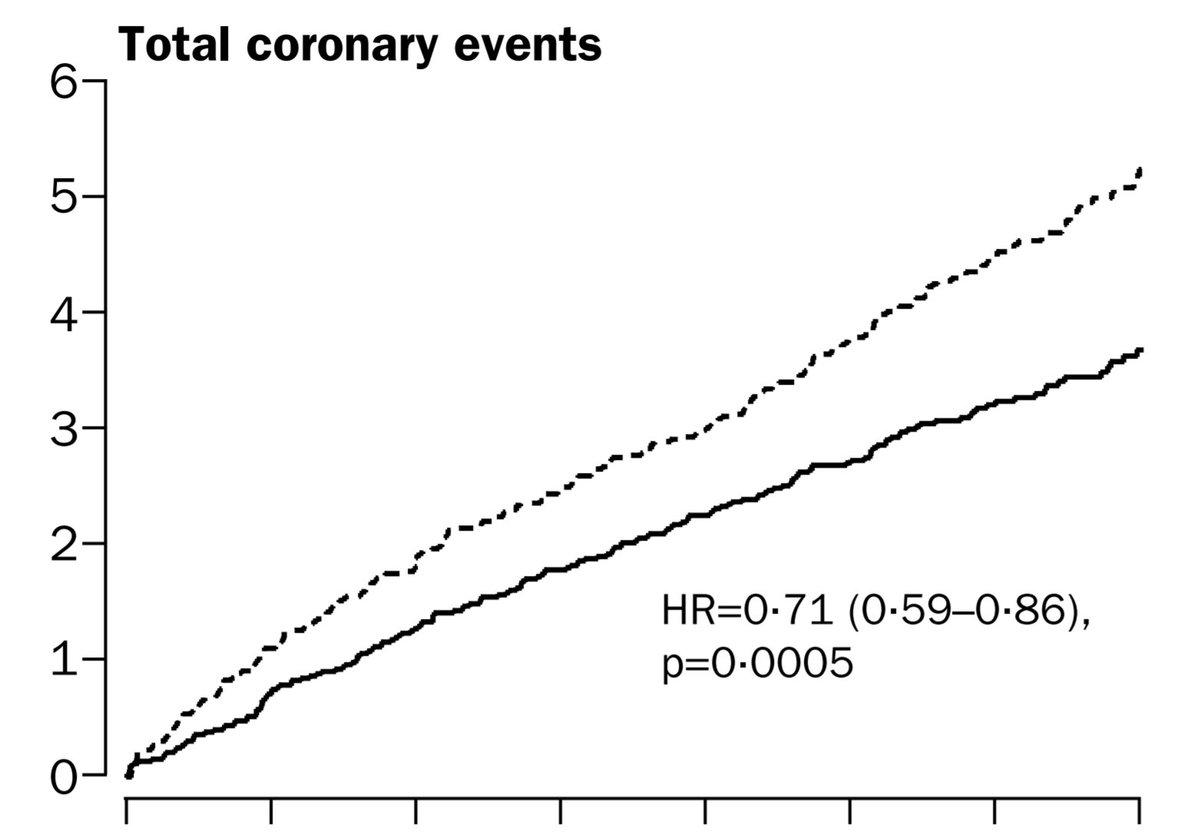
Below is the Zijlstra et al NEJM trial of Primary Angioplasty versus Streptokinase for acute MI. We all know how that turned out. It keeps us up at night. (Literally!)
Notice that the graphs are NOT scaled versions of each other.
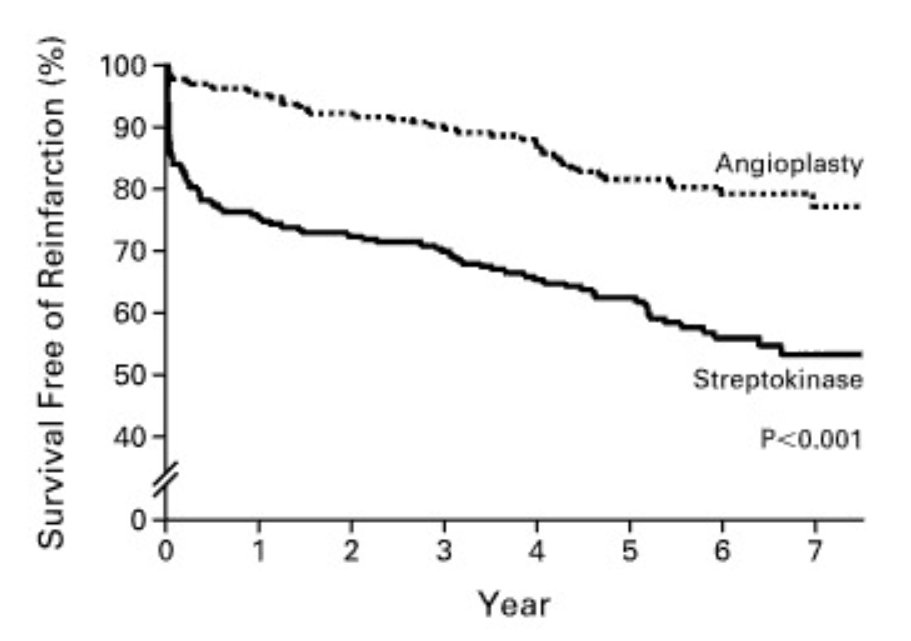
Here are the shapes of the event curves:
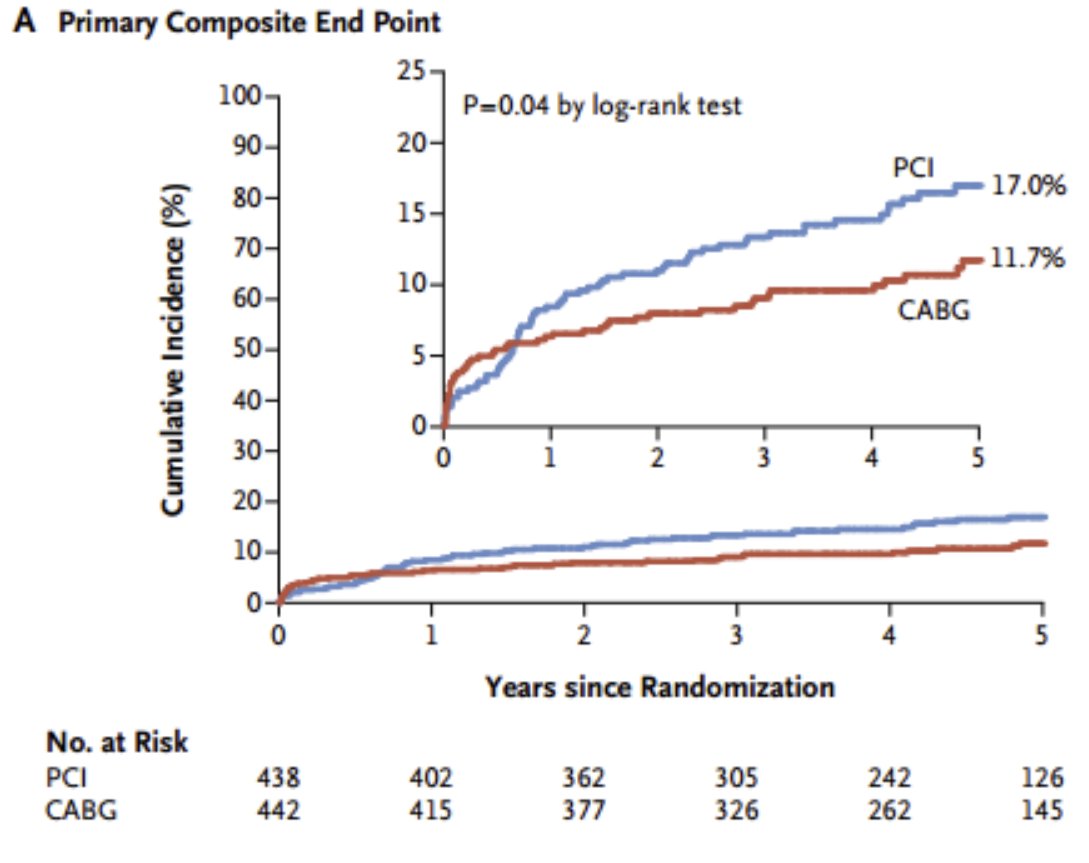
Look at other examples, and see. Is the pattern the same?
Is the same one always coming up at higher risk at the beginning, and lower risk later?
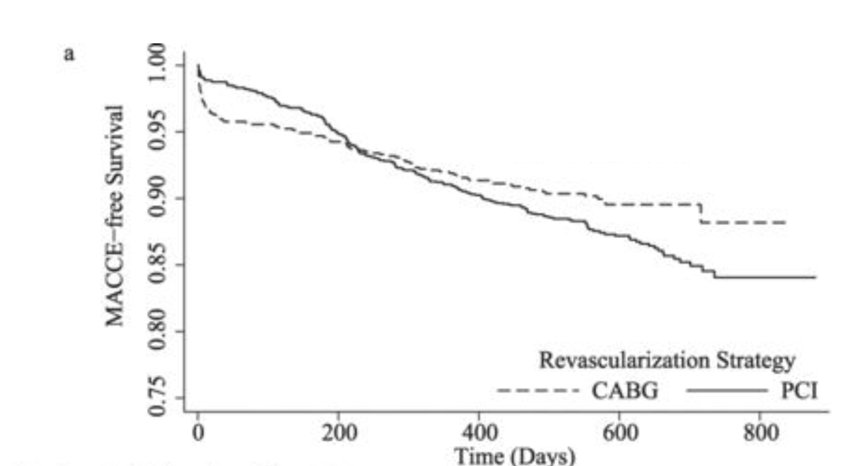
But as time passes, the CABG patients seem to accumulate events slower than the PCI patients.
The earlier your time window of observation, the more it looks like PCI is safer.
The longer you wait before starting to count events, the more it looks like CABG is safer.
But CABG-v-PCI is certainly not a simple proportional hazard.
Less torturous than most weekends, due to the jollifications Saturday night (happy birthday @rallamee!)
Another weekend I will look at Hazard Ratios per unit something e.g. per mmol/L cholesterol, or per kg weight, and how to interpret them.
😀