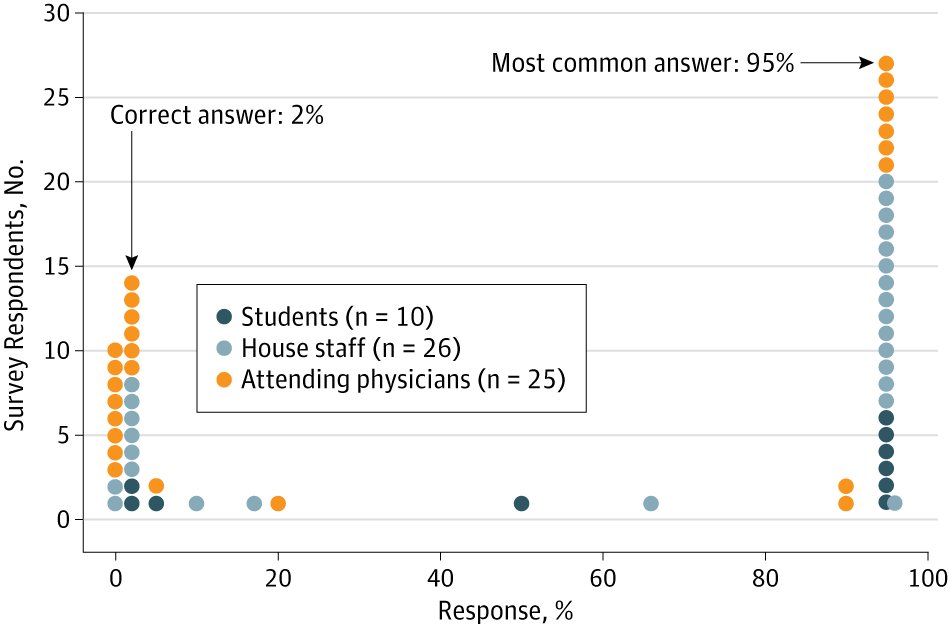
An otherwise healthy 40 year old woman comes to you after reading on the internet about a terrible disease that one in a thousand women get, and a highly accurate test that can save her life.
You order this test and it comes back positive. The woman anxiously asks you, do I have the disease? What is the chance this woman has the disease?
jamanetwork.com/journals/jamai…